We give simple and unified proofs of weak holomorhpic Morse inequalities on complete manifolds, $q$-convex manifolds, pseudoconvex domains, weakly $1$-complete manifolds and covering manifolds. This paper is essentially based on the asymptotic Bergman kernel functions and the Bochner-Kodaira-Nakano formulas.

In any dimension $N \geq 1$, for given mass a>0, we look to critical points of the energy functional $$I(u) = \frac{1}{2}\int_{\mathbb{R}^N}|\nabla u|^2 dx + \int_{\mathbb{R}^N}u^2|\nabla u|^2 dx - \frac{1}{p}\int_{\mathbb{R}^N}|u|^p dx$$ constrained to the set $$\mathcal{S}_a=\{ u \in X | \int_{\mathbb{R}^N}| u|^2 dx = a\},$$ where X:=\left\{u \in H^1(\mathbb{R}^N)\Big| \int_{\mathbb{R}^N} u^2|\nabla u|^2 dx <\infty\right\}. We focus on the mass super-critical case $$4+\frac{4}{N}0$when$1\leq N\leq 4$. For$N\geq 5$, we find an explicit number$a_0$such that the existence of minimizer is true if and only if$a\in (0, a_0]$. In the mass super-critical case, the existence of a minimizer to the problem $M_a$, or more generally the existence of a constrained critical point of $I$ on $\mathcal{S}_a$, had hitherto only been obtained by assuming that $p \leq 2^*$. In particular, the restriction $N \leq 3$ was necessary. We also study the asymptotic behavior of the minimizers to $M_a$ as the mass $a \downarrow 0$, as well as when $a \uparrow a^*$, where $a^*=+\infty$ for $1\leq N\leq 4$, while $a^*=a_0$ for $N\geq 5$.

Yui and Zagier made some fascinating conjectures on the factorization on the norm of the difference of Weber class invariants $ f(\mathfrak a_1) - f(\mathfrak a_2)$based on their calculation in \cite{YZ}. Here$\mathfrak a_i$ belong two diferent ideal classes of discrimants $D_i$ in imagainary quadratic fields $\mathbb{Q}(\sqrt{D_i})$. In \cite{LY}, we proved these conjectures and their generalizations when $(D_1, D_2) =1$ using the so-called big CM value formula of Borcherds lifting. In this sequel, we prove the conjectures when $\mathbb{Q}(\sqrt{D_1}) =\mathbb{Q}(\sqrt{D_2})$ using the so-called small CM value formula. In addition, we give a precise factorization formula for the resultant of two different Weber class invariant polynomials for distinct orders.

In this work, we establish modular parameterizations for two general formulas for $\frac{1}{\pi}$ that subsume conjectural Ramanujan type formulas due to Z.-W. Sun, which have remained open since 2011. As an application of this, in a conceptual way we interpret how Sun's conjectural formulas arise and can be verified, as well as recover other cases that were proved by Cooper, Wan and Zudilin.

The signs of Fourier coefficients of certain eta quotients are determined by dissecting expansions for theta functions and by applying a general dissection formula for certain classes of quintuple products. A characterization is given for the coefficient sign patterns for $$\frac{(q^i;q^i)_{\infty}}{(q^p;q^p)_{\infty}}$$ for integers $i > 1$ and primes $p > 3$. The sign analysis for this quotient addresses and extends a conjecture of Bringmann et al. for the coefficients of $(q^2;q^2)_{\infty}(q^5;q^5)_{\infty}^{-1}$. The sign distribution for additional classes of eta quotients is considered. This addresses multiple conjectures posed by Bringmann et al.

We use certain Morse functions to construct conformal metrics with negative sectional curvature on locally conformally flat manifolds with boundary. Moreover, without conformally flatness assumption, we also construct conformal metric of positive Einstein tensor.

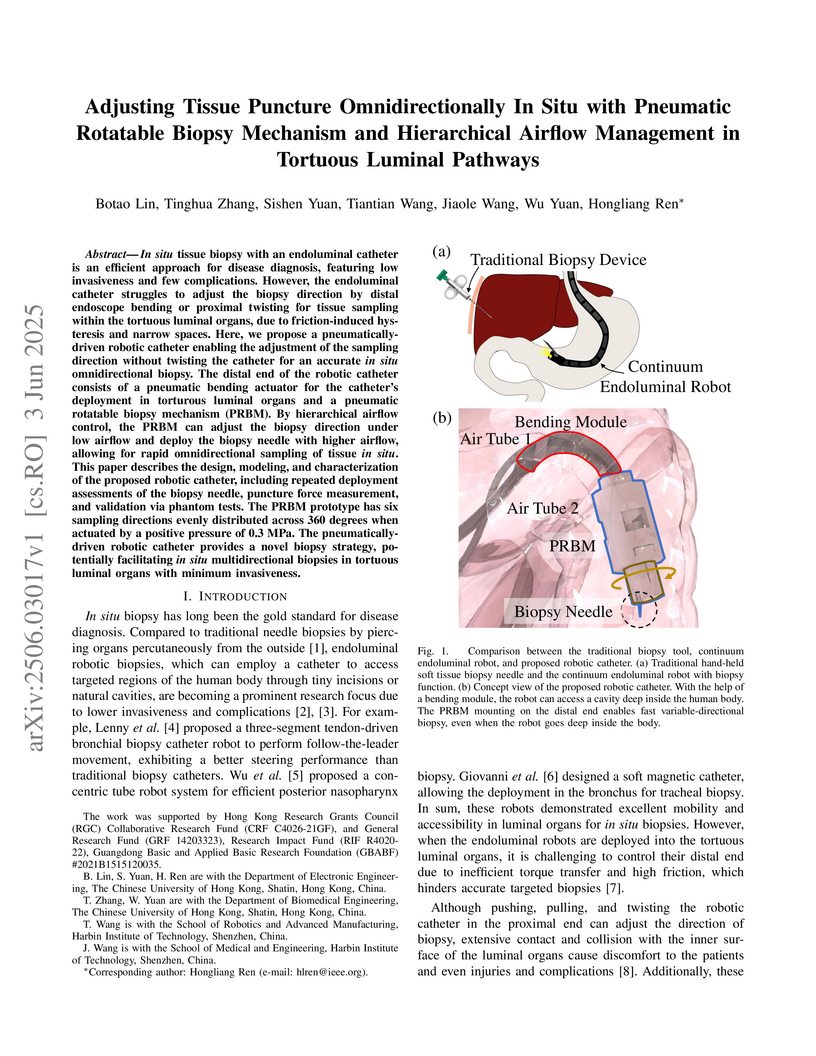
In situ tissue biopsy with an endoluminal catheter is an efficient approach for disease diagnosis, featuring low invasiveness and few complications. However, the endoluminal catheter struggles to adjust the biopsy direction by distal endoscope bending or proximal twisting for tissue sampling within the tortuous luminal organs, due to friction-induced hysteresis and narrow spaces. Here, we propose a pneumatically-driven robotic catheter enabling the adjustment of the sampling direction without twisting the catheter for an accurate in situ omnidirectional biopsy. The distal end of the robotic catheter consists of a pneumatic bending actuator for the catheter's deployment in torturous luminal organs and a pneumatic rotatable biopsy mechanism (PRBM). By hierarchical airflow control, the PRBM can adjust the biopsy direction under low airflow and deploy the biopsy needle with higher airflow, allowing for rapid omnidirectional sampling of tissue in situ. This paper describes the design, modeling, and characterization of the proposed robotic catheter, including repeated deployment assessments of the biopsy needle, puncture force measurement, and validation via phantom tests. The PRBM prototype has six sampling directions evenly distributed across 360 degrees when actuated by a positive pressure of 0.3 MPa. The pneumatically-driven robotic catheter provides a novel biopsy strategy, potentially facilitating in situ multidirectional biopsies in tortuous luminal organs with minimum invasiveness.