We study an analogue information paradox in acoustic black holes which are emerged from the superfluid surrounding a Schwarzschild black hole. The resulting acoustic black hole contains both acoustic horizons and optical horizon, with analogue Hawking radiation, i.e. phonons, emitted from the outer acoustic horizon. By using the island formula, we calculate the entanglement entropy of analogue Hawking radiation of the acoustic black hole in both non-extremal and extremal cases. In the non-extremal case, the entanglement entropy of phonons follow the Page curve due to the emergence of islands, and it is approximately proportional to the area of the acoustic horizon at late time. While in the extremal case, the entanglement entropy of phonons diverges, leading to an ill-defined Page time. Our study verifies the unitarity of the analogue gravity system, and provides further insight into the connection between the entanglement entropy and the causal structure of spacetime.

The remnant of a black hole binary merger settles into a stationary configuration by "ringing down" through the emission of gravitational waves that consist of a superposition of damped exponentials with discrete complex frequencies - the remnant black hole's quasinormal modes. While the frequencies themselves depend solely on the mass and spin of the remnant, the mode amplitudes depend on the merger dynamics. We investigate quasinormal mode excitation by a point particle plunging from the innermost stable circular orbit of a Kerr black hole. Our formalism is general, but we focus on computing the quasinormal mode excitation coefficients in the frequency domain for equatorial orbits, and we analyze their dependence on the remnant black hole spin. We find that higher overtones and subdominant multipoles of the radiation become increasingly significant for rapidly rotating black holes. This suggests that the prospects for detecting overtones and higher-order modes are considerably enhanced for highly spinning merger remnants.

Perturbative calculations of gravitational radiation near horizons of rotating black holes have been plagued with divergence issues. We derive for the first time a divergence-free source term for such cases within the generalized Sasaki-Nakamura formalism. As applications, we compute the dynamical deformation of the event horizon caused by an ultrarelativistic particle plunge, demonstrating the excitation of quasinormal modes at the horizon, and we evaluate the energy flux towards the horizon from an extreme mass-ratio inspiral. This framework provides a powerful tool for studying physics near black hole horizons.

We examine the origin of the cosmological collider signal using the framework of open effective field theories. Focusing on the single exchange of a massive scalar field, we demonstrate that the trispectrum splits cleanly into its local and non-local components once the heavy-field propagators are decomposed in the Keldysh basis. Integrating out the massive degree of freedom yields a single-field effective field theory for the light scalar that necessarily contains both unitary operators and non-unitary contributions associated with dissipation and stochastic noise. We show that the leading local signal in parity-preserving theories arises from the unitary part of this effective field theory, whereas the non-local signal is intrinsically associated with its stochastic sector. The effective field theory coefficients themselves are a priori non-analytic in the external kinematics; however, this non-analyticity can be softened when a scale hierarchy - such as the heavy-mass expansion - is imposed, up to spurious contributions that ultimately cancel in observables. Finally, we establish a connection between the cosmological collider signal and entropy production, linking the observable non-local signal to intrinsic properties of the quantum state, including its degree of mixedness.

In this paper, we create a Mellin space method for boundary correlation functions in de Sitter (dS) and anti-de Sitter (AdS) spaces. We demonstrate that the analytic continuation between AdS${}_{d+1}$ and dS${}_{d+1}$ is encoded in a set of simple relative phases using the Mellin-Barnes representation of correlators. It helps us to determine the scalar three-point and four-point functions and their corresponding Mellin-Barnes amplitudes in dS${}_{d+1}$ space using the known results from AdS${}_{d+1}$ space. The Mellin-Barnes representation reveals the analytic structure of boundary correlation functions over all $d$ and scaling dimensions. In the present discussion, the {\it split representation} have been used as an instrumental technique in particularly the evaluation of bulk Witten diagrams and is suitable to obtain the {\it Conformal Partial Wave decomposition} of tree-level exchange in the bulk Witten diagrams. The equivalent adjustment to the cosmological three-point and four-point function of generic external scalars may be further extracted from these results, assuming the weak breakdown of the de Sitter isometries. These findings offer a step towards a more methodical comprehension of de Sitter observables utilising Mellin space techniques at the tree level and beyond.

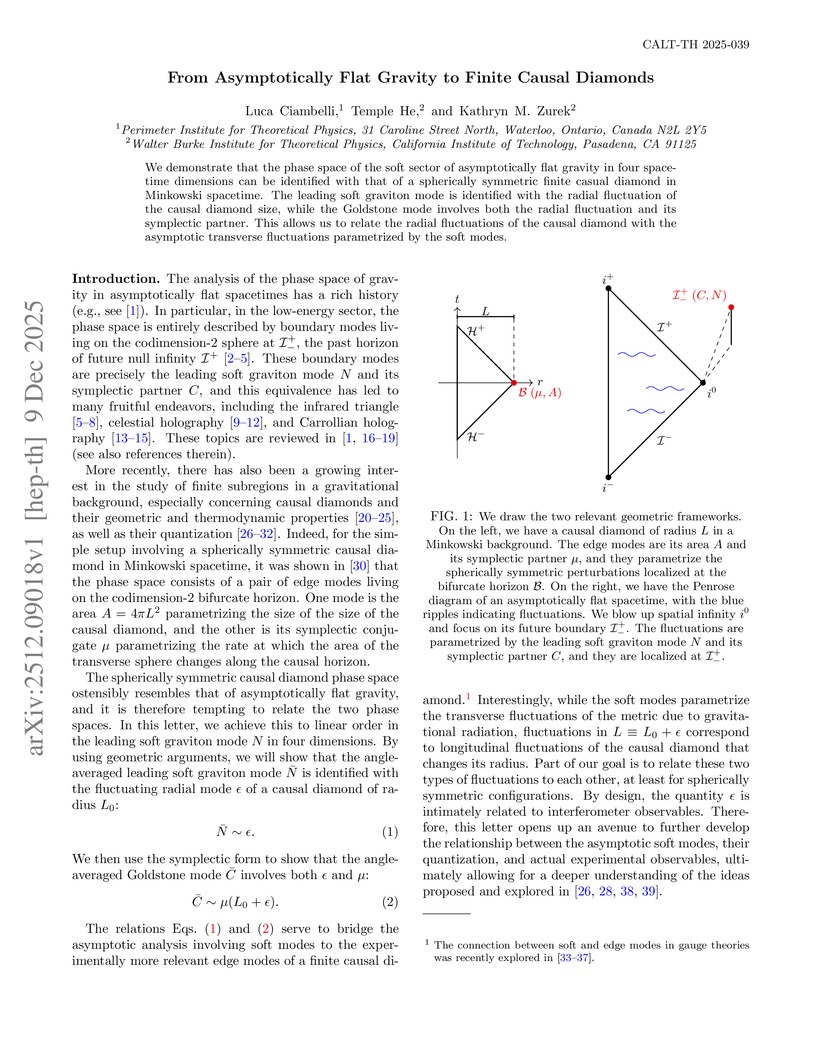
We demonstrate that the phase space of the soft sector of asymptotically flat gravity in four spacetime dimensions can be identified with that of a spherically symmetric finite casual diamond in Minkowski spacetime. The leading soft graviton mode is identified with the radial fluctuation of the causal diamond size, while the Goldstone mode involves both the radial fluctuation and its symplectic partner. This allows us to relate the radial fluctuations of the causal diamond with the asymptotic transverse fluctuations parametrized by the soft modes.

We investigate the constraints imposed by the Weak Gravity Conjecture (WGC) on gravitational lensing in gravity's rainbow, focusing in particular on scenarios beyond extremality and on the interplay between the WGC and the Weak Cosmic Censorship Conjecture (WCCC) in the context of Reissner-Nordström-Anti-de Sitter black holes modified by rainbow gravity. Using topological methods, we first analyze the configuration of photon spheres and confirm that unstable circular photon spheres with topological charge $(\omega = -1)$ exist outside the event horizon throughout the parameter space, thereby verifying the simultaneous validity of both the WGC and the WCCC. The rainbow functions $f(\varepsilon)$ and $g(\varepsilon)$, which encode Planck-scale corrections through the energy ratio $(\varepsilon =E/E_P)$, modify both the spacetime metric and the extremality bound. We derive the corresponding modified extremal charge-to-mass ratio, (q^2/m^2)>(Q^2/M^2)_{\text{ext}}, and show that gravity's rainbow offers a natural mechanism for reconciling these two fundamental conjectures. By applying the Gauss-Bonnet theorem in conjunction with Jacobi-Maupertuis optical geometry, we compute the weak deflection angles for both photons and massive particles to second order. The rainbow function $g(\varepsilon)$ appears with powers $(g^{-2})$ and $(g^{-4})$, enhancing the deflection angle when g(\varepsilon)<1, while $f(\varepsilon)$ influences only the charge-dependent contributions. At extremality, the deflection angle becomes independent of $f(\varepsilon)$, yielding a universal prediction that can be tested without specifying the form of the rainbow functions. We further find that super-extremal configurations exhibit stronger lensing effects than extremal black holes, suggesting a potential observational discriminator between WGC-satisfying naked singularities and WCCC-preserving black holes.

Time, space and entanglement are the main characters in this work. Their nature is still a great mystery in physics and we study here the possibility that these three phenomena are closely connected, showing how entanglement can be at the basis of the emergence of time and space within closed quantum systems. We revisit and extend the Page and Wootters theory that was originally introduced in order to describe the emergence of time through entanglement between subsystems in a globally static, quantum Universe. In the book, after providing a complete review of the salient aspects of the theory, we establish a connection with recent research on the foundations of statistical mechanics and we propose a new understanding of the thermalization process. Furthermore, we generalize the framework in order describe the spatial degree of freedom and we provide a model of 3+1 dimensional, quantum spacetime emerging from entanglement among different subsystems in a globally "timeless" and "positionless" Universe. Finally, via the Page and Wootters theory, the evolution of quantum clocks within a gravitational field is treated and a time dilation effect is obtained in agreement with the Schwarzschild solution.

We develop a mesoscopic framework in which the cosmological exterior is treated as an open quantum subsystem coupled to a horizon reservoir. Local conservation laws, expressed as $\nabla_\mu\langle J^\mu\rangle=0$, imply that when baryon number is lost across a horizon its conserved quantum numbers are sequestered into inaccessible modes, producing an effective depletion in the exterior sector. Global unitarity therefore requires compensating source terms in the exterior continuity equations. We show that relativity forces these compensating excitations to arise through long-wavelength geometric modes: only infrared fluctuations can restore entropy and charge while remaining outside the causal wedge of the infalling matter. This identifies an infrared return channel as a generic feature of horizon-coupled semiclassical gravity. The second ingredient is a Carnot-Carathéodory (CC) tangent geometry, whose mesoscopic scale $\sigma$ governs both the excitation of these IR modes and the kinematics of photon and matter propagation. In this setting, photon trajectories follow recurrent horizontal geodesics, producing an effective cosmic cavity whose stationary state is a Planck spectrum set by $\sigma$. The same scale modifies large-radius circular motions in a way consistent with flattened rotation curves. Horizon thermodynamics and mesoscopic balance laws then link $\sigma$ to the cosmic expansion rate, $H\sim\sigma$, yielding a unified infrared structure underlying photon equilibrium, baryon balance, and large-scale kinematics.

In this work, we investigate synchrotron emission and the observational signatures of anisotropic non-thermal electrons during magnetic-flux eruptions in a magnetically arrested disk, using 3D GRMHD simulations. Non-thermal electrons are assumed to be energized from the thermal background through magnetic reconnection, with pitch-angle distributions modeled as beamed or loss-cone types, alongside an isotropic case for comparison. The results show that non-thermal emission can produce pronounced flux outbursts and localized brightening during eruptions, while the associated increase in optical depth can suppress the linear polarization fraction. Introducing pitch-angle anisotropy further reshapes the angular distribution of the intrinsic emissivity and modulates its contribution to various observable signatures. Our results demonstrate that anisotropic non-thermal electrons are essential for a physically complete interpretation of black hole image variability.

Overtones are known to improve the performance of fits to the ringdown, both in numerical-relativity simulations and gravitational-wave observations. Although the overtone frequencies are a concrete prediction of general relativity, it remains an open question whether they are excited to the extent that fits would suggest. In this work, we take a pragmatic approach and investigate the practical utility of each additional overtone in extracting information from the ringdown. We look at the dependence of the ringdown start time on the number of overtones, and the feasibility of detecting deviations from general relativity in the ringdown frequencies. We suggest that there is no clear "maximum" overtone, but rather the utility of each additional overtone decreases compared to the one before. Finally, we perform Bayesian parameter estimation (as opposed to least-squares fits) to obtain posterior distributions on the overtone amplitudes and phases, allowing us to investigate their correlation structure. Due to strong correlations it becomes increasingly hard to measure individual amplitudes and phases for the highest overtones. However, we find that the joint measurement of overtone amplitudes (i.e., the correlation structure itself) is sensitive to the frequencies and decay times of even the highest overtones, possibly offering an avenue to perform consistency tests with general relativity.

Recoiling remnants of black-hole mergers in dense environments can produce bright electromagnetic (EM) counterparts to the gravitational-wave (GW) emission. Significance assessments of such GW-EM candidates are restricted to time and sky-localisation consistency, omitting the physics governing the EM emission process. Different emission mechanisms, however, impose different observability constraints on the remnant black-hole recoil and spin, which are gravitational-wave observables. We present a statistical framework that includes such parameters. We assess the consistency of the GW190521-ZTF19abanrhr pair with two types of emission processes: a Blandford-Znajek jet closely aligned with the final spin axis and a diffusive isotropic flare. Assuming the sky-location of ZTF19abanrhr, we find these mechanisms to be respectively strongly and moderately disfavoured with log-evidences $\log_{10}{\cal I}_{\rm jet} = -1.65$ and $\log_{10}{\cal I}_{\rm diff} = -0.075$. Combining these with odds for a common sky-location $\Omega$ we obtain respective combined odds $\log_{10} {\cal O}_{\Omega,{\rm jet}}= -1.17$ and $\log_{10} {\cal O}_{\Omega,{\rm diff}}= +0.39$ for a true GW-EM coincidence as opposed to a random one. Our method leverages a previously unexplored evidence axis to assess GW-EM associations and constrain both the physics powering flare mechanisms and the properties of AGNs.

Field space geometry plays a central role within the Swampland Programme, most notably in the various Distance Conjectures. However, for gravitational EFTs, this geometry is not uniquely defined: one can cast the action in many synonymous descriptions related by Weyl transformations, in which the field space metric transforms non-trivially across conformal frames. This raises a crucial question of how we are meant to think of the field space metric in view of employing the Swampland Conjectures. In this work we resolve this ambiguity by developing a fully frame-covariant framework for studying gravitational EFTs. We show that all conformal frames arise as distinct foliations of a singular higher-dimensional auxiliary geometry. Applying ADM formalism to the augmented field space, it is clear how Weyl- and unit transformations can be understood from a geometric point of view. Using this framework, we revisit the Species Scale Distance Conjecture and Sharpened Distance Conjecture, and show how the bounds derive from universal properties of gravitational EFTs under Weyl transformations. This strongly suggests that aspects of these conjectures apply to a much broader class of scalar-tensor theories and are consequences of frame covariance, rather than constraints imposed by quantum gravity.

We show how to coherently combine information from a population of sub-threshold, gravitational-wave binary neutron star post-merger remnants. Although no individual event in our synthetic population can be claimed as a confident detection, we show how to statistically determine the fraction of merger events that promptly collapse to form a black hole, compared to those for which a neutron star survives the merger for at least tens of milliseconds. This fraction, when combined with information about the neutron star mass distribution gleaned from the inspiral portion of the signals, provides an indirect measure of the neutron star maximum mass. Using conservative measures of the post-merger waveforms, we show that 50-70 events with binary neutron star inspiral measurements can be combined to give an $11-20\%$ fractional uncertainty on the maximum mass of rapidly rotating, hot neutron stars, which can potentially be turned into a $12-21\%$ fractional constraint on the Tolman-Oppenheimer-Volkoff mass. We discuss how this measure of the hot nuclear equation of state can be combined with information of cold neutron stars to see the effect of temperature on physics in the densest regions of the Universe.

In relativistic Astrophysics the $I$-Love-$Q$ relations refer to approximately EoS-independent relations involving the moment of inertia, Love number, and quadrupole moment through some quantities that are normalised by the mass $M_0$ of the background configuration of the perturbative scheme. Since $M_0$ is not an observable quantity, this normalisation hinders the direct applicability of the relations. A common remedy assumes that $M_0$ coincides with the actual mass of the star $M_S$; however, this approximation is only adequate for very slow rotation (when the dimensionless spin parameter is \chi_S<0.1). The more accurate alternative approach, based on the $I$-Love-$Q$-$\delta M$ set of relations, circumvents this limitation by enabling the inference of $M_0$. Here we review both approaches and provide numerical comparisons.

Direct-collapse black holes (DCBHs) are an important component of the massive black hole population of the early universe, and their formation and early mergers will be prominent in the data stream of the Laser Interferometer Space Antenna (LISA). However, the population and binary properties of these early black holes are poorly understood, with masses, mass ratios, spins, and orbital eccentricities strongly dependent on the details of their formation, and the properties of the remaining exterior material (baryonic and non-baryonic), which may be substantial to the point of merger. We report on initial work to simulate the formation, collapse, and/or merger of such DCBH regions in order to extract the resulting gravitational-wave signals.

Rotating black holes can form dense boson clouds through superradiant instability, making Kerr black holes a powerful probe of ultralight massive bosons. Previous studies of black hole superradiance have often treated bosonic fields classically, leaving open questions about how particles are produced and how the clouds grow over time. In this work, we canonically quantize a massive scalar field around a Kerr black hole, providing a fully quantum description of black hole superradiance. We show that the evolution of the particle number in the cloud, as well as the energy and angular momentum of the scalar field, can be consistently explained within the standard framework of quantum field theory in curved spacetime. Furthermore, we prove that the growth of the cloud occurs independently of the choice of initial state. We also explore several phenomena related to a massive scalar field in a rotating black hole spacetime, including Hawking radiation, adiabatic backreaction on the black hole spin, and the direction of level transitions in the presence of self-interactions of the field. Our analysis provides a consistent quantum-mechanical perspective that includes all these phenomena.

We introduce and study \emph{brachistochrone-ruled timelike surfaces} in Newtonian and relativistic spacetimes. Starting from the classical cycloidal brachistochrone in a constant gravitational field, we construct a Newtonian ``brachistochrone-ruled worldsheet'' whose rulings are time-minimizing trajectories between pairs of endpoints. We then generalize this construction to stationary Lorentzian spacetimes by exploiting the reduction of arrival-time functionals to Finsler- or Jacobi-type length functionals on a spatial manifold. In this framework, relativistic brachistochrones arise as geodesics of an associated Finsler structure, and brachistochrone-ruled timelike surfaces are timelike surfaces ruled by these time-minimizing worldlines. We work out explicit examples in Minkowski spacetime and in the Schwarzschild exterior: in the flat case, for a bounded-speed time functional, the brachistochrones are straight timelike lines and a simple family of brachistochrone-ruled surfaces turns out to be totally geodesic; in the Schwarzschild case, we show how coordinate-time minimization at fixed energy reduces to geodesics of a Jacobi metric on the spatial slice, and outline a numerical scheme for constructing brachistochrone-ruled timelike surfaces. Finally, we discuss basic geometric properties of such surfaces and identify natural Jacobi fields along the rulings.

We derive a kinetic Boltzmann equation characterizing the long-term statistical behavior of the turbulent dynamics of nonlinear interacting gravitational wave multipoles in Minkowski spacetime and show that, injecting a large number of gravitons with large multipoles drives the system toward an inverse multipole cascade at large times.

We consider the string-theory inspired Einstein-Maxwell-Maxwell-dilaton theory (EMMD) and show that we can derive the complete set of thermodynamic quantities of charged black holes, without having to solve for the black hole solutions. We argue that the technique can be applied more broadly to string theories, providing an accessible method for determining the thermodynamic properties of large classes of black holes for which exact solutions are typically unavailable.