It is shown that time-ordered correlation functions of a unitary CFT$_2$ in 2D Minkowski space admit a single-valued, conformally-invariant extension to the Lorentzian signature torus provided that the $S^1\times S^1$ spatial and temporal radii are equal. The result extends to Lorentzian CFT$_D$ on equal-radii $S^{D-1}\times S^1$ under the assumption that branch cuts occur only when a pair of operator insertions are null separated.

We study an analogue information paradox in acoustic black holes which are emerged from the superfluid surrounding a Schwarzschild black hole. The resulting acoustic black hole contains both acoustic horizons and optical horizon, with analogue Hawking radiation, i.e. phonons, emitted from the outer acoustic horizon. By using the island formula, we calculate the entanglement entropy of analogue Hawking radiation of the acoustic black hole in both non-extremal and extremal cases. In the non-extremal case, the entanglement entropy of phonons follow the Page curve due to the emergence of islands, and it is approximately proportional to the area of the acoustic horizon at late time. While in the extremal case, the entanglement entropy of phonons diverges, leading to an ill-defined Page time. Our study verifies the unitarity of the analogue gravity system, and provides further insight into the connection between the entanglement entropy and the causal structure of spacetime.

The asymptotic nature of perturbative expansions in quantum field theory can arise from the factorial growth in the number of Feynman diagrams with loop order, as with instantons, or from a series of individual diagrams whose values grow factorially, as with renormalon chains in QED. Other classes of diagrams are known also to grow factorially, such as the Hopf series of graphs in $\phi^3$ theory. This Hopf series was studied using Schwinger-Dyson equations and the Connes-Kreimer Hopf algebra of decorated rooted trees. We review the Hopf algebra approach and show that the same results can be obtained using analytic QFT techniques as with Hopf-algebraic ones. We present an efficient method to extract the asymptotic behavior and thereby generalize the analysis of the Hopf series to other classes of diagrams in other theories. We confront the question of whether these classes correspond to new types of asymptotic growth beyond instantons and renormalons, and find that they appear to be incomplete calculations of what would be renormalons in these theories if all diagrams were included. Although the Hopf algebra approach is not essential to deriving asymptotic behavior from Schwinger-Dyson equations, it does provide some other insights into quantum field theory. We therefore attempt also to provide a map between some relevant aspects of the Hopf algebra and quantum field theory.

We examine the origin of the cosmological collider signal using the framework of open effective field theories. Focusing on the single exchange of a massive scalar field, we demonstrate that the trispectrum splits cleanly into its local and non-local components once the heavy-field propagators are decomposed in the Keldysh basis. Integrating out the massive degree of freedom yields a single-field effective field theory for the light scalar that necessarily contains both unitary operators and non-unitary contributions associated with dissipation and stochastic noise. We show that the leading local signal in parity-preserving theories arises from the unitary part of this effective field theory, whereas the non-local signal is intrinsically associated with its stochastic sector. The effective field theory coefficients themselves are a priori non-analytic in the external kinematics; however, this non-analyticity can be softened when a scale hierarchy - such as the heavy-mass expansion - is imposed, up to spurious contributions that ultimately cancel in observables. Finally, we establish a connection between the cosmological collider signal and entropy production, linking the observable non-local signal to intrinsic properties of the quantum state, including its degree of mixedness.

Due to entropic effects, it is possible that generic high-energy states of a quantum or classical system are ordered. This leads to spontaneous symmetry breaking at arbitrarily high temperatures. We present minimal models of entropic order that arise from very simple interactions. Our main examples are the Arithmetic Ising Model (AIM) and its quantum analogue, where usual Ising spins are replaced by non-negative integers. Using a large-flavor expansion together with numerical simulations, we find that the high-temperature phase is ordered in the classical and quantum models. We also introduce classical gas models whose interactions drive the system to a crystal at high temperatures.

In this paper, we create a Mellin space method for boundary correlation functions in de Sitter (dS) and anti-de Sitter (AdS) spaces. We demonstrate that the analytic continuation between AdS${}_{d+1}$ and dS${}_{d+1}$ is encoded in a set of simple relative phases using the Mellin-Barnes representation of correlators. It helps us to determine the scalar three-point and four-point functions and their corresponding Mellin-Barnes amplitudes in dS${}_{d+1}$ space using the known results from AdS${}_{d+1}$ space. The Mellin-Barnes representation reveals the analytic structure of boundary correlation functions over all $d$ and scaling dimensions. In the present discussion, the {\it split representation} have been used as an instrumental technique in particularly the evaluation of bulk Witten diagrams and is suitable to obtain the {\it Conformal Partial Wave decomposition} of tree-level exchange in the bulk Witten diagrams. The equivalent adjustment to the cosmological three-point and four-point function of generic external scalars may be further extracted from these results, assuming the weak breakdown of the de Sitter isometries. These findings offer a step towards a more methodical comprehension of de Sitter observables utilising Mellin space techniques at the tree level and beyond.

We develop a procedure that reorganizes the perturbative expansion in a class of quantum field theories into a stringy amplitude expressed as a sum over two-dimensional geometries. Using Schwinger parametrization and the one-to-one correspondence between metric ribboned graphs and the moduli space of Riemann surfaces established via Strebel differentials, we map each Feynman diagram to a surface. We then construct a conformal field theory on the worldsheet whose correlation functions encode the full set of QFT Feynman rules directly from the geometry of the associated Riemann surface. Restoring diffeomorphism and Weyl invariance promotes the integral over moduli space to a path integral over worldsheet metrics, yielding a non-critical string theory whose Liouville mode naturally becomes a holographic direction. By construction, the expansion of the string theory amplitudes in the number of boundary state insertions matches the loop expansion in the QFT at fixed genus. Moreover, loop divergences are shown to match standard string-theoretic degeneration limits, indicating that gravitational backreaction is equivalent to QFT renormalization. Our construction provides a microscopic route from generic QFTs to emergent string theories and offers a framework for deriving holographic duals directly from field-theoretic data.

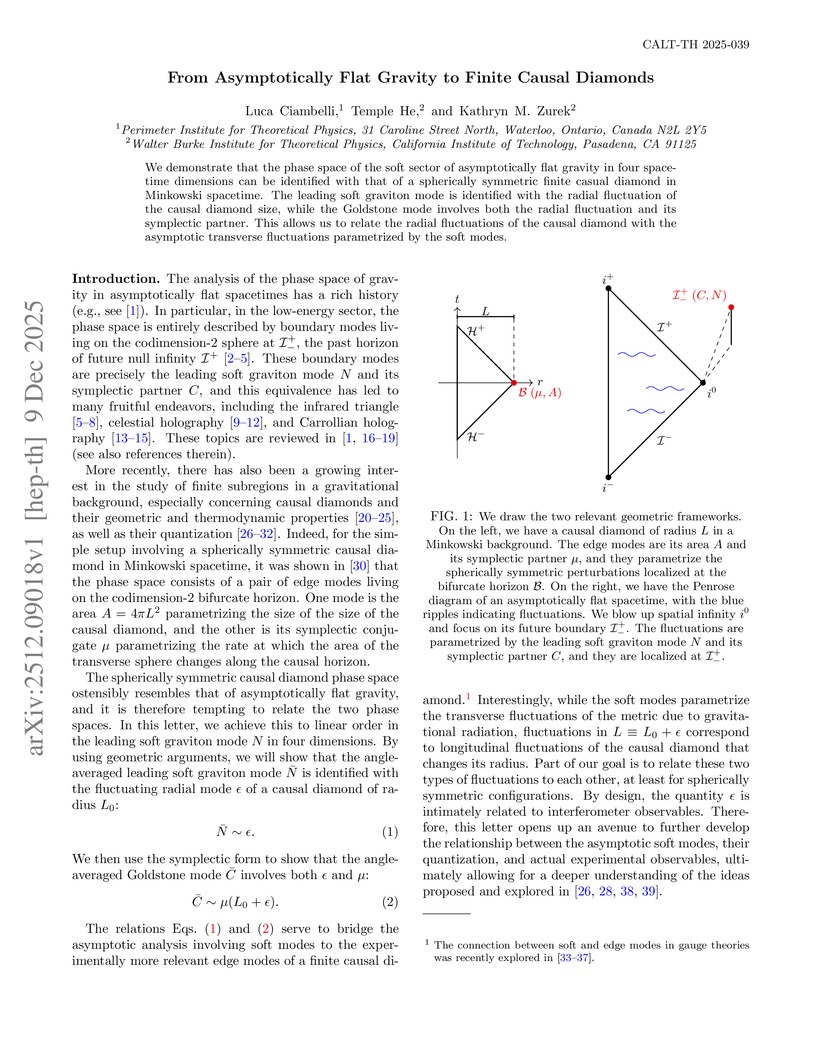
We demonstrate that the phase space of the soft sector of asymptotically flat gravity in four spacetime dimensions can be identified with that of a spherically symmetric finite casual diamond in Minkowski spacetime. The leading soft graviton mode is identified with the radial fluctuation of the causal diamond size, while the Goldstone mode involves both the radial fluctuation and its symplectic partner. This allows us to relate the radial fluctuations of the causal diamond with the asymptotic transverse fluctuations parametrized by the soft modes.

We investigate the constraints imposed by the Weak Gravity Conjecture (WGC) on gravitational lensing in gravity's rainbow, focusing in particular on scenarios beyond extremality and on the interplay between the WGC and the Weak Cosmic Censorship Conjecture (WCCC) in the context of Reissner-Nordström-Anti-de Sitter black holes modified by rainbow gravity. Using topological methods, we first analyze the configuration of photon spheres and confirm that unstable circular photon spheres with topological charge $(\omega = -1)$ exist outside the event horizon throughout the parameter space, thereby verifying the simultaneous validity of both the WGC and the WCCC. The rainbow functions $f(\varepsilon)$ and $g(\varepsilon)$, which encode Planck-scale corrections through the energy ratio $(\varepsilon =E/E_P)$, modify both the spacetime metric and the extremality bound. We derive the corresponding modified extremal charge-to-mass ratio, (q^2/m^2)>(Q^2/M^2)_{\text{ext}}, and show that gravity's rainbow offers a natural mechanism for reconciling these two fundamental conjectures. By applying the Gauss-Bonnet theorem in conjunction with Jacobi-Maupertuis optical geometry, we compute the weak deflection angles for both photons and massive particles to second order. The rainbow function $g(\varepsilon)$ appears with powers $(g^{-2})$ and $(g^{-4})$, enhancing the deflection angle when g(\varepsilon)<1, while $f(\varepsilon)$ influences only the charge-dependent contributions. At extremality, the deflection angle becomes independent of $f(\varepsilon)$, yielding a universal prediction that can be tested without specifying the form of the rainbow functions. We further find that super-extremal configurations exhibit stronger lensing effects than extremal black holes, suggesting a potential observational discriminator between WGC-satisfying naked singularities and WCCC-preserving black holes.

Spontaneous symmetry breaking is a cornerstone modern physics, defining a wealth of phenomena in condensed-matter and high-energy physics, and beyond. It requires an infinite number of degrees of freedom, and even then, for continuous symmetries, it only works if the spatial dimension is not too low, following the classic results of Coleman, Hohenberg, Mermin and Wagner. While usually discussed in the context of quantum and statistical field theories, and in particular, effective field theories, there are advantages in addressing the same kind of phenomena on discrete geometric structures rather than conventional manifolds. When the space is discretized into a lattice, a lucid picture of conventional spontaneous symmetry breaking springs up, with the ultraviolet issues of continuum quantum field theory out-of-sight, and the key effect, which is infrared in nature, revealed through elementary harmonic oscillator networks. From there, it is natural to generalize lattices to other graphs/networks. In this setting, the presence of spontaneous symmetry breaking is controlled by fractional generalizations of resistance distance and the Kirchhoff index, and most broadly by the spectral dimension. Predictably, because of richness of discrete geometric structures in comparison with continuous manifolds, a broader array of geometries emerge where spontaneous breaking of continuous symmetries is blocked by large fluctuations.

We describe the loop corrections to supercharges in supersymmetric quantum field theories using the holomorphic twist formalism. We begin by reviewing the relation between supercharge corrections and the "twice-generalized" Konishi anomaly, which corrects the semi-chiral ring. In the holomorphic twist, these corrections appear as BRST anomalies and are computed using the higher operations of an underlying $L_\infty$ conformal algebra. We then apply this formalism to obtain the complete one-loop corrections to the supercharge of four-dimensional Lagrangian supersymmetric gauge theories, including $\mathcal{N}=4$ SYM, where it admits a remarkably compact expression in terms of superfields.

We investigate the critical temperature of a relativistic Bose-Einstein condensate of charged bosons driven by rotation in a parallel magnetic field [Y. Liu and I. Zahed, Phys. Rev. Lett. {\bf120}, 032001 (2018)]. For non-interacting bosons, the critical temperature can only be determined for a system with fixed angular momentum. We find that the critical temperature of the non-interacting system vanishes due to the fact that the system is quasi-one-dimensional, indicating that non-interacting bosons cannot undergo Bose-Einstein condensation. For interacting bosons, we investigate a system with quartic self-interaction. We show that the order parameter vanishes and the off-diagonal long-range order is absent at any nonzero temperature because of the quasi-one-dimensional feature, in accordance with the Coleman-Mermin-Wagner-Hohenberg theorem.

Field space geometry plays a central role within the Swampland Programme, most notably in the various Distance Conjectures. However, for gravitational EFTs, this geometry is not uniquely defined: one can cast the action in many synonymous descriptions related by Weyl transformations, in which the field space metric transforms non-trivially across conformal frames. This raises a crucial question of how we are meant to think of the field space metric in view of employing the Swampland Conjectures. In this work we resolve this ambiguity by developing a fully frame-covariant framework for studying gravitational EFTs. We show that all conformal frames arise as distinct foliations of a singular higher-dimensional auxiliary geometry. Applying ADM formalism to the augmented field space, it is clear how Weyl- and unit transformations can be understood from a geometric point of view. Using this framework, we revisit the Species Scale Distance Conjecture and Sharpened Distance Conjecture, and show how the bounds derive from universal properties of gravitational EFTs under Weyl transformations. This strongly suggests that aspects of these conjectures apply to a much broader class of scalar-tensor theories and are consequences of frame covariance, rather than constraints imposed by quantum gravity.

Rotating black holes can form dense boson clouds through superradiant instability, making Kerr black holes a powerful probe of ultralight massive bosons. Previous studies of black hole superradiance have often treated bosonic fields classically, leaving open questions about how particles are produced and how the clouds grow over time. In this work, we canonically quantize a massive scalar field around a Kerr black hole, providing a fully quantum description of black hole superradiance. We show that the evolution of the particle number in the cloud, as well as the energy and angular momentum of the scalar field, can be consistently explained within the standard framework of quantum field theory in curved spacetime. Furthermore, we prove that the growth of the cloud occurs independently of the choice of initial state. We also explore several phenomena related to a massive scalar field in a rotating black hole spacetime, including Hawking radiation, adiabatic backreaction on the black hole spin, and the direction of level transitions in the presence of self-interactions of the field. Our analysis provides a consistent quantum-mechanical perspective that includes all these phenomena.

We investigate the impact of particle production during inflation in scenarios where an infinite tower of states features a mass scale that decreases exponentially along the inflationary trajectory. Such couplings naturally arise in string effective field theories and are in fact motivated by the Swampland Distance Conjecture (SDC). We show that the corrections to inflationary observables sourced by the tower scale as $(H/\Lambda_{\text{sp}})^{2+p}$, with $H$ being the Hubble scale, $\Lambda_{\text{sp}}$ being the species scale, that is the quantum gravity cut-off, and $p\geq 1$ characterizes the density of states in the tower. As a result, in gravitationally weakly coupled cosmological effective theories, the tower-induced contributions are suppressed relative to the standard single-field predictions, leaving the inflationary phenomenology essentially unchanged. We demonstrate this explicitly across a set of well-motivated inflationary potentials, and we compare the resulting predictions with the most recent observational constraints, including those from the Atacama Cosmology Telescope.

We derive a kinetic Boltzmann equation characterizing the long-term statistical behavior of the turbulent dynamics of nonlinear interacting gravitational wave multipoles in Minkowski spacetime and show that, injecting a large number of gravitons with large multipoles drives the system toward an inverse multipole cascade at large times.