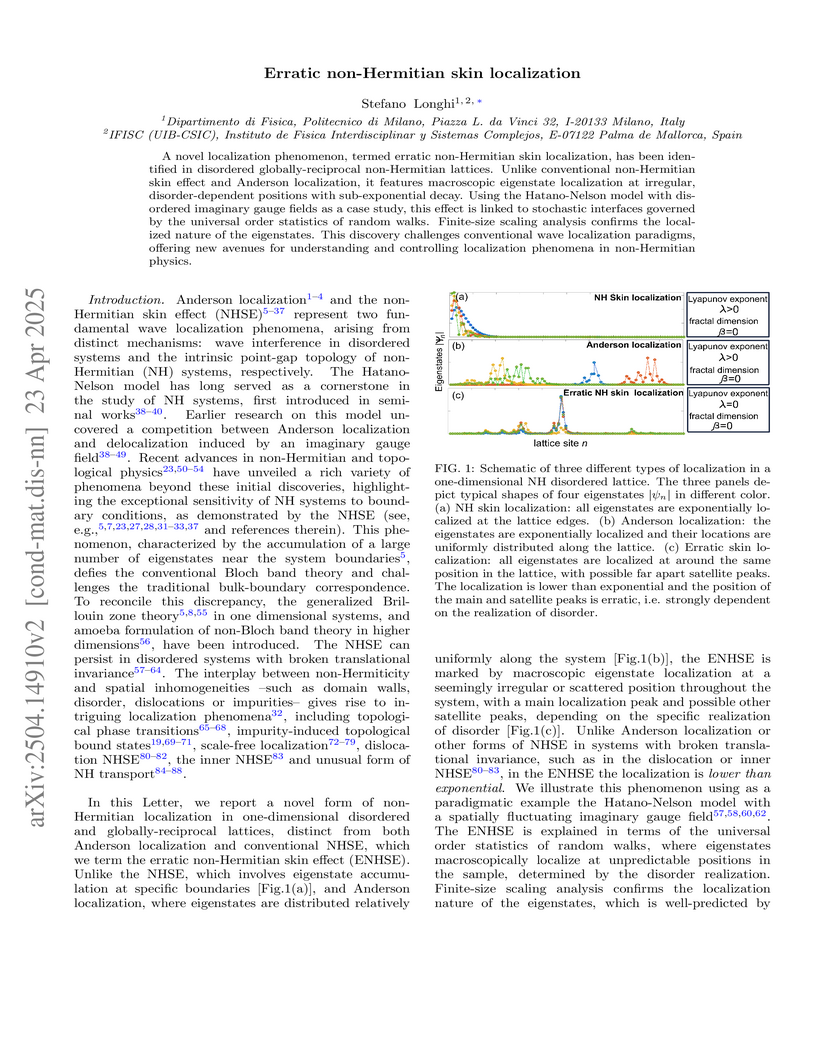
A novel localization phenomenon, termed erratic non-Hermitian skin localization, has been identified in disordered globally-reciprocal non-Hermitian lattices. Unlike conventional non-Hermitian skin effect and Anderson localization, it features macroscopic eigenstate localization at irregular, disorder-dependent positions with sub-exponential decay. Using the Hatano-Nelson model with disordered imaginary gauge fields as a case study, this effect is linked to stochastic interfaces governed by the universal order statistics of random walks. Finite-size scaling analysis confirms the localized nature of the eigenstates. This discovery challenges conventional wave localization paradigms, offering new avenues for understanding and controlling localization phenomena in non-Hermitian physics.

We show the emergence of spontaneous synchronization between a pair of detuned quantum oscillators within a harmonic network. Our model does not involve any nonlinearity, driving, or external dissipation, thus providing the simplest scenario for the occurrence of local coherent dynamics in an extended harmonic system. A sufficient condition for synchronization is established by building upon the Rayleigh normal mode approach to vibrational systems. Our results show that mechanisms favoring synchronization, even between oscillators that are not directly coupled to each other, are transient energy depletion and crosstalk. We also address the possible buildup of quantum correlations during synchronization and show that indeed entanglement may be generated in detuned systems, starting from uncorrelated states and without any direct coupling between the two oscillators.

Understanding the temporal dependence of precipitation is key to improving weather predictability and developing efficient stochastic rainfall models. We introduce an information-theoretic approach to quantify memory effects in discrete stochastic processes and apply it to daily precipitation records across the contiguous United States. The method is based on the predictability gain, a quantity derived from block entropy that measures the additional information provided by higher-order temporal dependencies. This statistic, combined with a bootstrap-based hypothesis testing and Fisher's method, enables a robust memory estimator from finite data. Tests with generated sequences show that this estimator outperforms other model-selection criteria such as AIC and BIC. Applied to precipitation data, the analysis reveals that daily rainfall occurrence is well described by low-order Markov chains, exhibiting regional and seasonal variations, with stronger correlations in winter along the West Coast and in summer in the Southeast, consistent with known climatological patterns. Overall, our findings establish a framework for building parsimonious stochastic descriptions, useful when addressing spatial heterogeneity in the memory structure of precipitation dynamics, and support further advances in real-time, data-driven forecasting schemes.

The random walk of photons in a tight-binding lattice is known to exhibit diffusive motion similar to classical random walks under decoherence, clearly illustrating the quantum-to-classical transition. In this study, we reveal that the random walk of intense classical light under dephasing dynamics can disentangle quantum and ensemble averaging, making it possible to observe a subdiffusive walker dynamics, i.e. a behavior very distinct from both a classical and a quantum walker. These findings are demonstrated through proposing photonic random walks in synthetic temporal lattices, based on pulse dynamics in coupled fiber loops.

A unique feature of non-Hermitian (NH) systems is the NH skin effect, i.e. the edge localization of an extensive number of bulk-band eigenstates in a lattice with open or semi-infinite boundaries. Unlike extended Bloch waves in Hermitian systems, the skin modes are normalizable eigenstates of the Hamiltonian that originate from the intrinsic non-Hermitian point-gap topology of the Bloch band energy spectra. Here we unravel a fascinating property of NH skin modes, namely self-healing, i.e. the ability to self-reconstruct their shape after being scattered off by a space-time potential.

In lattices with uncorrelated on-site potential disorder, Anderson localization near the band edges can exhibit anomalously weak localization in the form of Lifshitz tail states. These states correspond to clusters of contiguous sites with nearly identical on-site energies, allowing excitations to extend significantly beyond the characteristic localization length determined by the inverse of Lyapunov exponent. Since Lifshitz tail states are rare events, with an exponentially small density of states, they are typically considered of limited practical importance. In this work, we demonstrate that when Anderson localization is induced by disorder in an imaginary on-site potential, Lifshitz tail states can dominate the system's dynamics and become experimentally observable. This phenomenon is illustrated through the Anderson-Bernoulli model in a non-Hermitian photonic lattice, shedding light on the unique interplay between disorder and non-Hermiticity in such systems

Network theory has played a dominant role in understanding the structure of complex systems and their dynamics. Recently, quantum complex networks, i.e. collections of quantum systems in a non-regular topology, have been explored leading to significant progress in a multitude of diverse contexts including, e.g., quantum transport, open quantum systems, quantum communication, extreme violation of local realism, and quantum gravity geometries. However, the question on how to produce and control general quantum complex networks in experimental laboratory has remained open. Here we propose an all optical and reconfigurable implementation of quantum complex networks. The experimental proposal is based on optical frequency combs, parametric processes, pulse shaping and multimode measurements allowing the arbitrary control of the number of the nodes (optical modes) and topology of the links (interactions between the modes) within the network. Moreover, we also show how to simulate quantum dynamics within the network combined with the ability to address its individual nodes. To demonstrate the versatility of these features, we discuss the implementation of two recently proposed probing techniques for quantum complex networks and structured environments. Overall, our general method for implementing quantum complex networks with reconfigurable set-up has potential to define an experimental playground for designing and controlling complex networks -- and dynamics therein -- for several quantum physical frameworks.

It has long been recognized that emission of radiation from atoms is not an intrinsic property of individual atoms themselves, but it is largely affected by the characteristics of the photonic environment and by the collective interaction among the atoms. A general belief is that preventing full decay and/or decoherence requires the existence of dark states, i.e., dressed light-atom states that do not decay despite the dissipative environment. Here, we show that, contrary to such a common wisdom, decoherence suppression can be intermittently achieved on a limited time scale, without the need for any dark state, when the atom is coupled to a chiral ring environment, leading to a highly non-exponential staircase decay. This effect, that we refer to as intermittent decoherence blockade, arises from periodic destructive interference between light emitted in the present and light emitted in the past, i.e., from delayed coherent quantum feedback.

Anderson localization, i.e. the suppression of diffusion in lattices with random or incommensurate disorder, is a fragile interference phenomenon which is spoiled out in the presence of dephasing effects or fluctuating disorder. As a consequence, Anderson localization-delocalization phase transitions observed in Hermitian systems, such as in one-dimensional quasicrystals when the amplitude of the incommensurate potential is increased above a threshold, are washed out when dephasing effects are included. Here we consider localization-delocalization spectral phase transitions occurring in non-Hermitian quasicrystals with local incommensurate gain and loss, and show that, contrary to the Hermitian case, the non-Hermitian phase transition is robust against dephasing effects. The results are illustrated by considering synthetic quasicrystals in photonic mesh lattices.

The Mpemba effect is the counterintuitive phenomenon in statistical physics for which a far-from-equilibrium state can relax toward equilibrium faster than a state closer to equilibrium. This effect has raised a great curiosity since long time and has been studied extensively in many classical and quantum systems. Here it is shown that the Mpemba effect can be observed in optics as well. Specifically, the process of light diffusion in finite-sized photonic lattices under incoherent (dephasing) dynamics is considered. Rather surprisingly, it is shown that certain highly-localized initial light distributions can diffuse faster than initial broadly delocalized distributions. The effect is illustrated by considering random walk of optical pulses in fiber-based temporal mesh lattices, which should provide an experimentally-accessible setup for the demonstration of the Mpemba effect in optics.

The Mpemba effect refers to the surprising observation where, under certain conditions, a far-from-equilibrium state can relax toward equilibrium faster than a state closer to equilibrium. A paradigmatic example is provided by the curious fact that hot water can sometimes freeze faster than cold water. The Mpemba effect has intrigued scientists since long time and has been predicted and observed in a variety of classical and quantum systems. Recently, the search for Mpemba-like effects of purely quantum nature has raised a major interest. Here we predict the emergence of Mpemba effect in the quantum optics context exploiting non-classical states of light. By analyzing the decay dynamics of photon fields in a leaky optical resonator or waveguide, it is demonstrated that bosonic Mpemba effect emerges in the context of the quantum nature of light. Specifically, the relaxation dynamics is strongly influenced by the photon statistics of the initially trapped light field. The Mpemba effect is observed when comparing the decay dynamics of classical light fields (coherent states) with certain non-classical states, such as Fock states, squeezed states and Schrödinger cat states.

Mosaic lattice models have been recently introduced as a special class of disordered systems displaying resonance energies, multiple mobility edges and anomalous transport properties. In such systems on-site potential disorder, either uncorrelated or incommensurate, is introduced solely at every equally-spaced sites within the lattice, with a spacing $M \geq 2$. A remarkable property of disordered mosaic lattices is the persistence of extended states at some resonance frequencies that prevent complete Anderson localization, even in the strong disorder regime. Here we introduce a broader class of mosaic lattices and derive general expressions of mobility edges and localization length for incommensurate sinusoidal disorder, which generalize previous results [Y. Wang {\it et al.}, Phys. Rev. Lett. {\bf 125}, 196604 (2020)]. For both incommensurate and uncorrelated disorder, we prove that Anderson localization is protected by the open gaps of the disorder-free lattice, and derive some general criteria for complete Anderson localization. The results are illustrated by considering a few models, such as the mosaic Su-Schrieffer-Heeger (SSH) model and the trimer mosaic lattice.

The behavior of systems far from equilibrium is often complex and unpredictable, challenging and sometimes overturning the physical intuition derived from equilibrium scenarios. One striking example of this is the Mpemba effect, which implies that non-equilibrium states can sometimes relax more rapidly when they are further from equilibrium. Despite a rich historical background, the precise conditions and mechanisms behind this phenomenon remain unclear. Recently, there has been growing interest in investigating accelerated relaxation and Mpemba-like effects within quantum systems. In this work, we explore a quantum manifestation of the Mpemba effect in a simple and paradigmatic model of open quantum systems: the damped quantum harmonic oscillator, which describes the relaxation of a bosonic mode in contact with a thermal bath at finite temperature $T$. By means of an exact analytical analysis of the relaxation dynamics based on the method of moments in both population and coherence subspaces, we demonstrate that any initial distribution of populations with the first $r$ moments exactly matching those of the equilibrium distribution shows a super-accelerated relaxation to equilibrium at a rate linearly increasing with $r$, leading to a pronounced Mpemba effect. In particular, one can find a broad class of far-from-equilibrium distributions that relax to equilibrium faster than any other initial thermal state with a temperature $T'$ arbitrarily close to $T$. The super-accelerated relaxation effect is shown to persist even for a broad class of initial states with non-vanishing coherences, and a general criterion for the observation of super-accelerated thermalization is presented.

The Hatano-Nelson model is a cornerstone of non-Hermitian physics, describing asymmetric hopping dynamics on a one-dimensional lattice, which gives rise to fascinating phenomena such as directional transport, non-Hermitian topology, and the non-Hermitian skin effect. It has been widely studied in both classical and quantum systems, with applications in condensed matter physics, photonics, and cold atomic gases. Recently, nonlinear extensions of the Hatano-Nelson model have opened a new avenue for exploring the interplay between nonlinearity and non-Hermitian effects. Particularly, in lattices with open boundary conditions, nonlinear skin modes and solitons, localized at the edge or within the bulk of the lattice, have been predicted. In this work, we examine the nonlinear extension of the Hatano-Nelson model with periodic boundary conditions and reveal a novel dynamical phenomenon arising from the modulational instability of nonlinear plane waves: growth blockade. This phenomenon is characterized by the abrupt halt of norm growth, as observed in the linear Hatano-Nelson model, and can be interpreted as a stopping of convective motion arising from self-induced disorder in the lattice.

Echo chamber effects in social networks are generally attributed to the prevalence of interactions among like-minded peers. However, recent evidence has emphasized the role of hostile interactions between opposite-minded groups. We investigate the role of polarization, identified with structural balance, in the formation of echo chambers in signed networks. To do so, we generalize the Independent Cascade Model and the Linear Threshold Model to describe information propagation in presence of negative edges. Antagonistic connections do not disrupt the flow of information, but instead, alter the way information is framed. Our results show that echo chambers spontaneously emerge in balanced networks, but also in antibalanced ones for specific parameters. This highlights that structural polarization and echo chambers do not necessarily display a one-to-one correspondence, showing instead a complex and often counterintuitive interplay. The robustness of our results is confirmed with a complex contagion model and through simulations in different network topologies, including real-world datasets.

This work explores the emergence of Mpemba-like effects within the quantum theory of lasers. By examining the temporal dynamics of photon number statistics in a single-mode laser above threshold, we reveal the curious and counterintuitive possibility that a laser system, starting with photon statistics far from equilibrium, may reach its stationary nearly-Poissonian distribution faster than a system initially closer to equilibrium. Drawing parallels to both classical and quantum Mpemba effects, we suggest that this behavior results from the unique relaxation dynamics of photon states, which is described by a non-integrable birth-death process. Our findings offer new insights into the foundational aspects of quantum laser light and contribute to the expanding body of research on non-equilibrium phenomena in quantum systems.

In waveguide quantum electrodynamics systems, atomic radiation emission is shaped by the photonic environment and collective atom interactions, offering promising applications in quantum technologies. In particular, atom-photon bound states, inhibiting complete spontaneous decay of the atom, can be realized through waveguide dispersion engineering or by utilizing giant atoms. While steady-state bound states are well understood, transient or virtual bound states remain less explored. Here we investigate transient atom-photon bound states, arising from initial atom-photon entanglement, and propose methods to slow down spontaneous atomic decay.

Carbon quantum dots (CQDs) are a promising material for electronic applications due to their easy fabrication and interesting semiconductor properties. Further, CQDs exhibit quantum confinement and charging effects, which may lead not only to improved performances but also to devices with novel functionalities. Here, we investigate the electronic transport of CQDs embedded on epoxy polymer. Our samples are coupled to interdigitated electrodes with individually addressable microelectrodes. Remarkably, the current-voltage characteristics show strongly nonlinear regimes at room temperature, ranging from Schottky diode to Coulomb blockade and even negative differential conductance behavior. We propose a master equation theoretical framework which allows us to compute current curves that agree well with the observations. This model emphasizes the importance of interacting dots and electron traps in generating a cohesive picture that encompasses all transport regimes. Overall, our results suggest that CQDs constitute a versatile materials platform for 3D integrated electronic purposes.

When a quantum dot is attached to a metallic reservoir and a superconducting contact Andreev processes leads to a finite subgap current at the normal lead and the creation or destruction of Cooper pairs. Andreev-reflection engines profit from the destruction of Cooper pairs to provide the work needed to set a charge current at the normal-conductor contact generating electrical power. For this power-transduction device high power and large efficiencies in quantum-mechanically enhanced regimes are demonstrated. There thermodynamic trade-off relations between power, efficiency and stability, valid for any classical engine are overcome, and kinetic constraints on the engine precision are largely surpassed in arbitrary far from equilibrium conditions.