State-of-the-art superconducting qubits rely on a limited set of thin-film materials. Expanding their materials palette can improve performance, extend operating regimes, and introduce new functionalities, but conventional thin-film fabrication hinders systematic exploration of new material combinations. Van der Waals (vdW) materials offer a highly modular crystalline platform that facilitates such exploration while enabling gate-tunability, higher-temperature operation, and compact qubit geometries. Yet it remains unknown whether a fully vdW superconducting qubit can support quantum coherence and what mechanisms dominate loss at both low and elevated temperatures in such a device. Here we demonstrate quantum-coherent merged-element transmons made entirely from vdW Josephson junctions. These first-generation, fully crystalline qubits achieve microsecond lifetimes in an ultra-compact footprint without external shunt capacitors. Energy relaxation measurements, together with microwave characterization of vdW capacitors, point to dielectric loss as the dominant relaxation channel up to hundreds of millikelvin. These results establish vdW materials as a viable platform for compact superconducting quantum devices.

We study the radiative heat transfer through a Su-Schrieffer-Heeger chain of plasmonic InSb nanoparticles in close vicinity of an InSb substrate. We show how the frequency bands of the in-plane and out-of-plane modes in the chain are deformed by the coupling to the surface waves in the InSb substrate by considering different carrier concentrations. By calculating the Zak phase we show that also in the presence of the substrate there is a topological phase transition and that topologically protected edge modes emerge for finite chains. Finally, we demonstrate the long-range heat transport along the chain due to the coupling to the surface waves of the sample. We find an enhanced heat transfer in the topological non-trivial phase compared to the trivial phase due to the contribution of the edge modes.

Quantum point contacts (QPC) are a key instrument in investigating the physics of edge excitations in the quantum Hall effect. However, at not-so-high bias voltage values, the predictions of the conventional point QPC model often deviate from the experimental data both in the integer and (more prominently) in the fractional quantum Hall regime. One of the possible explanations for such behaviors is the dependence of the tunneling between the edges on energy, an effect not present in the conventional model. Here we introduce two models that take QPC spatial extension into account: wide-QPC model that accounts for the distance along which the edges are in contact; long-QPC model accounts for the fact that the tunneling amplitude originates from a finite bulk gap and a finite distance between the two edges. We investigate the predictions of these two models in the integer quantum Hall regime for the energy dependence of the tunneling amplitude. We find that these two models predict opposite dependences: the amplitude decreasing or increasing away from the Fermi level. We thus elucidate the effect of the QPC geometry on the energy dependence of the tunneling amplitude and investigate its implications for transport observables.

Transport measurements are a powerful way to probe the electronic structure of quantum materials, but the information they contain is often convoluted. Yet, in particular for simple low-energy fermiologies, and by combining linear and non-linear responses, definite conclusion can be drawn -- such as, for instance, in the case of the circular photogalvanic effect in Weyl semimetals. Here, we derive the complete DC intrinsic transport response functions up to third order in the applied electric field within Boltzmann theory that hold combined information about quantum geometry and band dispersion. We discuss the responses for multifold fermions at high-symmetry momenta in time-reversal symmetric crystals as well as their reduction by symmetry constraints. We exemplify in detail the cases of space group 213 and space group 199, which realize different multifold fermions, and show under which conditions these low-energy excitations can be differentially addressed through their bulk nonlinear responses, enabling nonlinear valley-tronics.

Wigner crystals are a paradigmatic form of interaction driven electronic order. A key open question is how Berry curvature and, more generally, quantum geometry reshape crystallization. The discovery of two-dimensional materials with relatively flat bands and pronounced Berry curvature has added fresh urgency to this question. Recent mean-field studies have proposed a topological variant of the Wigner crystal, the anomalous Hall crystal (AHC), with non-zero Chern number. However it remains unclear whether the AHC survives beyond the mean-field approximation. Here, we map out the ground-state phase diagram of the $\lambda$-jellium model - a simple model whose interaction strength and Berry curvature are independently tunable - using state-of-the-art neural-network variational Monte Carlo. The AHC is found to remain stable against quantum fluctuations. Surprisingly, quantum geometric effects are found to dramatically enhance crystallization. Both the AHC and the standard Wigner Crystal are stabilized at densities up to an order of magnitude above the critical density in the absence of quantum geometry, yet still significantly below the threshold predicted by mean-field theory. These striking results highlight the rich interplay between quantum fluctuations, quantum geometry, and crystallization, providing concrete guidance for experiments and enabling future explorations of fractionalized crystals and chiral superconductors.

Quantum geometric formulations of linear and nonlinear responses can be constructed from a single building block in the form of a gauge-invariant interband transition operator. Here, we identify a second building block for quantum geometry: a band-resolved adiabatic connection operator that captures the noncommutativity between band projectors and their momentum derivatives. The band-resolved adiabatic connection operator, first introduced in the theory of adiabatic driving, serves as a generalized angular momentum within the state manifold of single bands, and we employ it to reformulate expressions for the band-resolved orbital magnetic moment. This form provides a complementary geometric interpretation alongside the multiband separation between energetic- and quantum-state properties by the two-state Berry curvature. Our formalism allows us to present formulas valid for both nondegenerate and degenerate bands, thereby removing the limitations of the common Bloch-state formula. We illustrate our theory by calculating a large orbital magnetization emerging without spin-orbit coupling in a spin-compensated, noncoplanar anomalous Hall magnet with degenerate bands.

Supersolidity, combining superfluid and crystalline orders, has been realized in dipolar Bose-Einstein condensates by tuning interatomic interactions. Here we show that supersolidity can also emerge from mode coupling at a superfluid-solid interface, without modifying bulk interactions and for a broad class of superfluids. Using an analytical and numerical treatment of the coupled superfluid and phonon fields, we derive the criterion for a density-modulation instability driven by interfacial coupling and dependent on dimensionality. In superfluid helium, the instability first appears at the roton mode, while in a Bose-Einstein condensate with contact interactions it occurs at the lowest accessible wave vector set by the system size. Beyond the threshold, the ground state acquires an interfacial density modulation while the bulk remains superfluid, forming a hybrid superfluid-supersolid phase. Our results identify interfacial mode coupling as a promising route to supersolidity, enabling the simultaneous exploitation of interfacial supersolid and bulk superfluid quantum properties.

The emergent Weyl modes with the broken time-reversal symmetry or inversion symmetry provide large Berry curvature and chirality to carriers, offering the realistic platforms to explore topology of electrons in three-dimensional systems. However, the reversal transition between different types of Weyl modes in a single material, which is of particular interest in the fundamental research in Weyl physics and potential application in spintronics, is scarcely achieved due to restriction of inborn symmetry in crystals. Here, by tuning the direction and strength of magnetic field in an ideal Dirac semimetal, Bi4(Br0.27I0.73)4, we report the realization of multiple Weyl modes, including gapped Weyl mode, Weyl nodal ring, and coupled Weyl mode by the magnetoresistivity measurements and electronic structure calculations. Specifically, under a magnetic field with broken mirror symmetry, anomalous Hall effect with step feature results from the large Berry curvature for the gapped Weyl mode. A prominent negative magnetoresistivity is observed at low magnetic field with preserved mirror symmetry and disappears at high magnetic field, which is correlated to the chiral anomaly and its annihilation of Weyl nodal ring, respectively. Our findings reveal distinct Weyl modes under the intertwined crystal symmetry and time-reversal breaking, laying the foundation of manipulating multiple Weyl modes in chiral spintronic network.

We theoretically investigated the readout process of a spin--qubit structure based on a gate-all-around (GAA) transistor. Our study focuses on a logical qubit composed of two physical qubits. Different spin configurations result in different charge distributions, which subsequently influence the electrostatic effects on the GAA transistor. Consequently, the current flowing through the GAA transistor depends on the qubit's state. We calculated the current-voltage characteristics of the three-dimensional configurations of the qubit and GAA structures, using technology computer-aided design (TCAD) simulations. Moreover, we performed circuit simulations using the Simulation Program with Integrated Circuit Emphasis (SPICE) to investigate whether a readout circuit made from complementary metal--oxide semiconductor (CMOS) transistors can amplify the weak signals generated by the qubits. Our findings indicate that, by dynamically controlling the applied voltage within a properly designed circuit, the readout can be detected effectively based on a conventional sense amplifier.

We introduce a driven-dissipative Floquet model in which a single harmonic oscillator with modulated frequency and decay realizes a non-Hermitian synthetic lattice with an effective electric field gradient in frequency space. Using the Floquet-Green's function and its doubled-space representation, we identify a topological regime that supports directional amplification and frequency conversion, accurately captured by a local winding number. The underlying mode structure is well described by a Jackiw-Rebbi-like continuum theory with Dirac cones and solitonic zero modes in synthetic frequency. Our results establish a simple and experimentally feasible route to non-Hermitian topological amplification, naturally implementable in current quantum technologies such as superconducting circuits.

We introduce a non-perturbative framework for quantizing chiral solitons in interacting quantum spin chains. This approach provides a direct lattice extension of the well-established $S$-duality between the sine-Gordon and Thirring models, thereby bridging the gap between continuum dualities and their lattice counterparts. By constructing the quantum chiral-soliton operators explicitly, we show how their unconventional dynamics appear in the excitation spectrum and correlation functions across the full Brillouin zone. A key result is that the dominant soliton tunneling amplitude alternates in sign, $\operatorname{sgn}(t_{1+}) = (-1)^{2S+1}$, sharply distinguishing half-odd-integer from integer spin chains. We further identify characteristic signatures of these chiral excitations in the dynamical spin structure factor, demonstrating their visibility in inelastic neutron scattering. Our results open a route to experimentally probing non-perturbative features of dual quantum field theories in condensed-matter settings.

Van der Waals heterostructures are a core tool in quantum material design. The recent addition of monolayer ferroelectrics expands the possibilities of designer materials. Ferroelectric domains can be manipulated using electric fields, thus opening a route for external control over material properties. In this paper we explore the possibility of engineering magneto-electric coupling in ferroelectric heterostructures by studying the interface of bilayer SnTe with iron phthalocyanine molecules as a model system. The molecules act as sensor spins, allowing us to sample the magneto-electric coupling with nanometer precision through scanning tunneling microscopy. Our measurements uncover a structural, and therefore material-independent and intrinsic, mechanism to couple electric and magnetic degrees of freedom at the nanoscale.

Using scanning tunneling microscopy-induced luminescence (STML), the optical properties of two-dimensional (2D) semiconductors may be investigated at the nanoscale. This is possible because the tunneling current under the tip is an extremely localized electrical excitation source. However, in most STML applications, the spatial distribution of the emission relative to the excitation point is unresolved. Yet this distribution contains key information about how the interaction of excitons with injected charge carriers affects the luminescence of these materials, and about exciton transport. Resolving this spatial distribution at the nanoscale is relevant both for a fundamental understanding of exciton physics and for device applications; yet it remains a significant challenge. In this work, we resolve the spatial distribution of the emission beyond the diffraction limit of light by deconvolving real-space optical microscopy images of the STML using an iterative algorithm, i.e., Richardson-Lucy (RL) deconvolution. To showcase this technique, we apply it to the STML of monolayer tungsten diselenide ($\mathrm{WSe_2}$) and tungsten disulfide ($\mathrm{WS_2}$). Thus, we highlight hitherto ignored or misunderstood aspects of STML on 2D semiconductors related to exciton and charge carrier transport, namely the dependence of the spatial distribution of emission on the tunnel current setpoint and the origin of the emission from hot spots located micrometers from the excitation source.

Long-range moire patterns in twisted WSe2 enable a built-in, moire-length-scale ferroelectric polarization that can be directly harnessed in electronic devices. Such a built-in ferroic landscape offers a compelling means to enable ultralow-voltage and non-volatile electronic functionality in two-dimensional materials; however, achieving stable polarization control without charge trapping has remained a persistent challenge. Here, we demonstrate a moire-engineered ferroelectric field-effect transistor (FeFET) utilizing twisted WSe2 bilayers that leverages atomically clean van der Waals interfaces to achieve efficient polarization-channel coupling and trap-suppressed, ultralow-voltage operation (subthreshold swing of 64 mV per decade). The device exhibits a stable non-volatile memory window of 0.10 V and high mobility, exceeding the performance of previously reported two-dimensional FeFET and matching that of advanced silicon-based devices. In addition, capacitance-voltage spectroscopy, corroborated by self-consistent Landau-Ginzburg-Devonshire modeling, indicates ultrafast ferroelectric switching (~0.5 microseconds). These results establish moire-engineered ferroelectricity as a practical and scalable route toward ultraclean, low-power, and non-volatile 2D electronics, bridging atomistic lattice engineering with functional device architectures for next-generation memory and logic technologies.

Two-dimensional (2D) Dirac fermions occur ubiquitously in condensed matter systems from topological phases to quantum critical points. Since the advent of topological semimetals, where the dispersion is often tilted around the band crossing where the Dirac fermion can appear, tilt has emerged as a key handle that controls physical properties. We study how tilt affects the transport and spectral properties of tilted 2D Dirac fermions under scalar disorder. Although our spectral analyses always show conformity to appropriate Gaussian ensembles, suggestive of delocalization, the conductivity scaling $g(L)$ shows a surprising richness. For a single Dirac node, relevant for quantum Hall transitions and topological insulator surface states, we find $g(L)\sim a_1\log(L)$ with a tilt-dependent coefficient a_1>0. Interestingly, when the tilt and transport directions are aligned, $a_1$ and hence $g(L)$ shows a spike at the critical point between the type-I and type-II regimes of the Dirac node. For systems with two Dirac nodes with unbroken time-reversal symmetry, pertinent to quasi-2D Dirac materials, we find $g(L)\sim L^{a_1}(\log L)^{a_2}$. However, we find a surprising tension between tilt along and perpendicular to the transport directions. For the former, $a_1$ changes sign as a function of tilt, hinting at a tilt-driven localization-delocalization transition, while a_1<0 for all tilts in the latter case, implying localization. These localized behaviors also reveal tension with the delocalization seen in spectral properties and suggest differing localization tendencies in real and Hilbert spaces. Overall, our work identifies tilt as an essential control parameter that uncovers rich and unconventional transport physics in 2D Dirac materials.

The energy levels and optical transitions of tetrahedral core/shell InP/ZnSe quantum dots (QDs) are investigated by means of multi-band k$\cdot$p theory. Despite the $\overline{T}_d$ symmetry relaxing spherical selection rules, the near-band-edge excitonic spectrum is reminiscent of that obtained for spherical nanocrystals. Exceptions appear in large (red-emitting) QDs, where transitions violating the (quasi-)angular momentum selection rule ($\Delta L=0,\pm 2$) are observed, and the ground state does not become dark ($P_{3/2}$-like). Valence band coupling is important in determining the symmetry, degeneracy and energy of hole states, with split-off holes playing a greater role than in CdSe QDs. The ($1S_e$-like) electron ground state exhibits moderate delocalization into the ZnSe shell. The confinement regime is then strong even for thick shells, which results in Coulomb interactions being mostly perturbative. Electrons remain largely localized in the InP core even in negative trions, despite electron-electron repulsions. At the same time, the asymmetry between Coulomb attractions and repulsions leads to negative (positive) trions being bound (antibound) by tens of meV. The biexciton binding energy switches from positive to negative, depending on the QD size.

Based on \textit{ab initio} screened configuration interaction calculations we find that TiI$_2$ has a bright exciton ground state and identify two key mechanisms that lead to this unprecedented feature among transition metal dichalcogenides. First, the spin-orbit induced conduction band splitting results in optically allowed spin-alignment for electrons and holes across a significant portion of the Brillouin zone around the $\mathbf{K}$-valley, avoiding band crossings seen in materials like monolayer MoSe$_2$. Second, a sufficiently weak exchange interaction ensures that the bright exciton remains energetically below the dark exciton state. We further show that the bright exciton ground state is stable under various mechanical strains and that trion states (charged excitons) inherit this bright ground state. Our findings are expected to spark further investigation into related materials that bring along the two key features mentioned, as bright ground-state excitons are crucial for applications requiring fast radiative recombination.

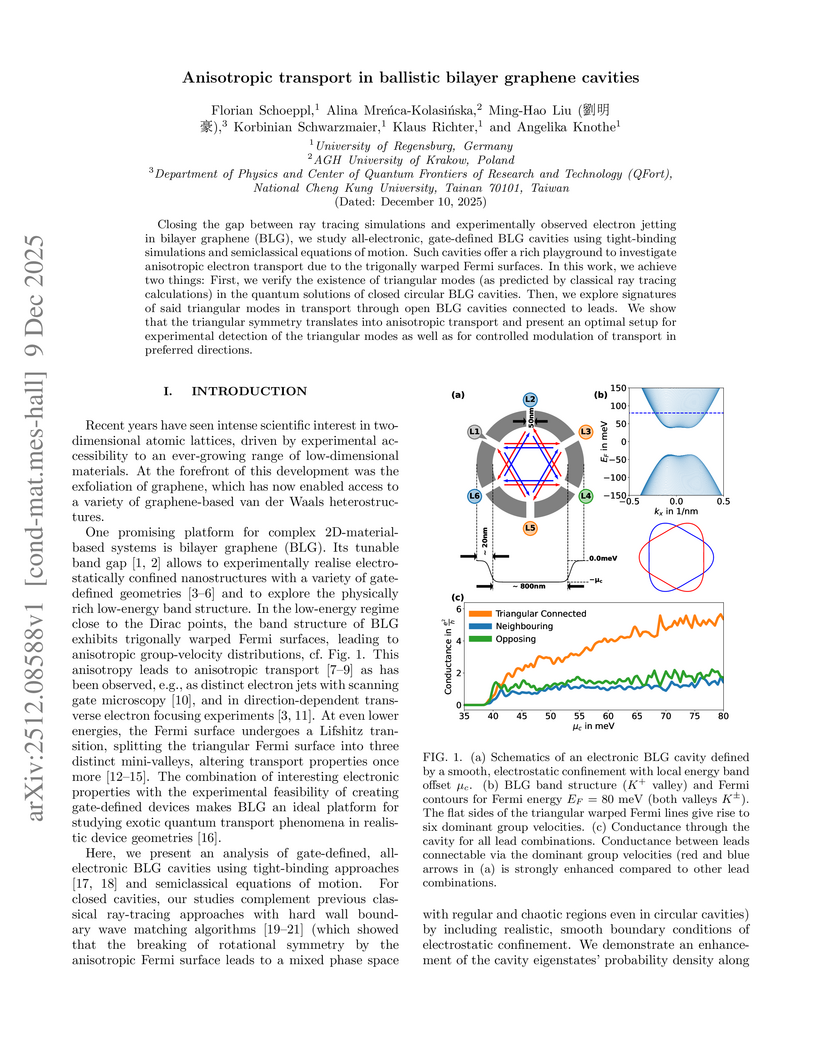
Closing the gap between ray tracing simulations and experimentally observed electron jetting in bilayer graphene (BLG), we study all-electronic, gate-defined BLG cavities using tight-binding simulations and semiclassical equations of motion. Such cavities offer a rich playground to investigate anisotropic electron transport due to the trigonally warped Fermi surfaces. In this work, we achieve two things: First, we verify the existence of triangular modes (as predicted by classical ray tracing calculations) in the quantum solutions of closed circular BLG cavities. Then, we explore signatures of said triangular modes in transport through open BLG cavities connected to leads. We show that the triangular symmetry translates into anisotropic transport and present an optimal setup for experimental detection of the triangular modes as well as for controlled modulation of transport in preferred directions.

The ideal altermagnets are a class of collinear, crystal-symmetry-enforced fully compensated magnets with nonrelativistic spin-split bands, in which contributions from Berry curvature to magneto-optical effects (MOEs) are strictly forbidden by an effective time-reversal symmetry. Here we show that, in such systems, MOEs are exclusively induced by the quantum metric and, in realistic altermagnets, are typically dominated by it. We refer to Berry-curvature-induced MOEs as conventional MOEs and to quantum-metric-dominated MOEs as unconventional MOEs. We derive general formulas that incorporate both Berry curvature and quantum metric for unconventional MOEs in altermagnets, enabling a quantitative evaluation of their respective contributions. Through symmetry analysis, we prove that ideal altermagnets are constrained to exhibit only unconventional MOEs. Using the three-dimensional canonical altermagnet MnTe and the emerging two-dimensional bilayer twisted altermagnet CrSBr as illustrative examples, we demonstrate that unconventional MOEs are prevalent in altermagnets. Our results establish altermagnets as a natural platform for quantum-metric-driven optical phenomena, substantially broadening the scope of MOEs and providing concrete predictions that can be tested in future experimental studies.

We explore the relation between quantum geometry in non-Hermitian systems and physically measurable phenomena. We highlight various situations in which the behavior of a non-Hermitian system is best understood in terms of quantum geometry, namely the notion of adiabatic potentials in non-Hermitian systems and the localization of Wannier states in periodic non-Hermitian systems. Further, we show that the non-Hermitian quantum metric appears in the response of the system upon time-periodic modulation, which one can use to experimentally measure the non-Hermitian quantum metric. We validate our results by providing numerical simulations of concrete exemplary systems.