Wigner crystals are extremely fragile, which is shown to result from very strong geometric frustration germane to long-range Coulomb interactions. Physically, this is manifested by a very small characteristic energy scale for shear density fluctuations, which are gapless excitations in a translationally invariant system. The presence of disorder, however, breaks translational invariance, thus suppressing gapless excitations and pushing them to higher density. We illustrate this general principle by explicit microscopic model calculations, showing that this mechanism very effectively stabilizes disordered Wigner lattices to much higher temperatures and densities than in the clean limit. On the other hand, we argue that in two dimensions disorder significantly ``smears" the melting transition, producing spatial coexistence of solid-like and liquid-like regions -- just as recently observed in STM experiments. Our results paint a new physical picture for melting of Wigner-Mott solids in two dimensions, corresponding to a Mott-Hubbard model with spatially varying local electronic bandwidth.

The behavior of the paradigmatic $J_1-J_2$ triangular lattice Heisenberg antiferromagnet in a magnetic field remains unsettled despite decades of study. We map out the phase diagram using three complementary approaches, including self-consistent nonlinear spin-wave theory, density-matrix renormalization group, and variational Monte Carlo. This combined analysis resolves the competition among different field-induced magnetic orders and magnetization plateaux across the classically frustrated parameter range. In particular, there is a finite range in the parameter regime around $J_2/J_1=\frac{1}{8}$ in which i) upon the application of the external field, the gapless quantum spin liquid acquires a finite density of monopoles, and ii) by further increasing the field, two plateaux are clearly obtained at $m=\frac{1}{3}$ and $m=\frac{1}{2}$. We discuss the experimental importance of the consecutive magnetization plateaux transitions as a signature of an underlying quantum spin-liquid phase.

Relaxation processes in topological phases such as quantum spin liquids are controlled by the dynamics and interaction of fractionalized excitations. In layered materials hosting two-dimensional topological phases, elementary quasiparticles can diffuse freely within the layer, whereas only pairs (or more) can hop between layers - a fundamental consequence of topological order. Using exact solutions of emergent nonlinear diffusion equations and particle-based stochastic simulations, we explore how pump-probe experiments can provide unique signatures of the presence of $2d$ topological excitations in a $3d$ material. Here we show that the characteristic time scale of such experiments is inversely proportional to the initial excitation density, set by the pump intensity. A uniform excitation density created on the surface of a sample spreads subdiffusively into the bulk with a mean depth $\bar z$ scaling as $\sim t^{1/3}$ when annihilation processes are absent. The propagation becomes logarithmic, $\bar z \sim \log t$, when pair-annihilation is allowed. Furthermore, pair-diffusion between layers leads to a new decay law for the total density, $n(t) \sim (\log^2 t)/t$ - slower than in a purely $2d$ system. We discuss possible experimental implications for pump-probe experiments in samples of finite width.

Quantum point contacts (QPC) are a key instrument in investigating the physics of edge excitations in the quantum Hall effect. However, at not-so-high bias voltage values, the predictions of the conventional point QPC model often deviate from the experimental data both in the integer and (more prominently) in the fractional quantum Hall regime. One of the possible explanations for such behaviors is the dependence of the tunneling between the edges on energy, an effect not present in the conventional model. Here we introduce two models that take QPC spatial extension into account: wide-QPC model that accounts for the distance along which the edges are in contact; long-QPC model accounts for the fact that the tunneling amplitude originates from a finite bulk gap and a finite distance between the two edges. We investigate the predictions of these two models in the integer quantum Hall regime for the energy dependence of the tunneling amplitude. We find that these two models predict opposite dependences: the amplitude decreasing or increasing away from the Fermi level. We thus elucidate the effect of the QPC geometry on the energy dependence of the tunneling amplitude and investigate its implications for transport observables.

Using determinant Quantum Monte Carlo, we investigate the interplay between doping, inter-layer tunneling and onsite Hund's coupling in stabilizing superconductivity (SC) in a two-orbital model for the bilayer Nickelate $\text{La}_3\text{Ni}_2\text{O}_7$. With realistic dispersion and for certain values of the interaction parameters, the auxiliary-field-decoupled fermion Hamiltonian has Kramers anti-unitary symmetries which guarantee the absence of a sign problem. The same anti-unitary symmetries can also be used to show there is a second instability towards $(\pi,\pi)$ exciton condensation in the strong interaction limit. We indicate the possible connection between this exciton order and the enigmatic density wave state observed in experiment, and clarify the decisive role played by the inter-layer tunneling in the competition between SC and exciton condensation. Finally, possible directions on how to enhance the SC transition temperature and stabilize the SC phase are also discussed.

To understand the intricate exchange between electrons of different bands in strongly correlated materials, it is essential to treat multi-orbital models accurately. For this purpose, dynamical mean-field theory (DMFT) provides an established framework, whose scope crucially hinges on the availability of efficient quantum impurity solvers. Here we present a real-frequency impurity solver based on neural quantum states (NQS) combined with an operator-Lanczos construction. NQS are an asymptotically unbiased variational ground-state ansatz that employs neural networks to capture long-range correlations on complicated graph structures. We leverage this ability to solve multi-orbital impurity problems using a systematically improvable Segmented Commutator Operator-Lanczos (SCOL) construction. Our benchmarks on both the single-orbital Anderson model and the multi-orbital Hubbard-Kanamori impurity Hamiltonian reveal excellent ground-state precision and the capacity to accurately resolve zero temperature spectral functions and self-energies. These results open avenues for extending DMFT to more challenging problems.

We propose a protocol to construct atypical high-energy eigenstates in quantum systems by using ground states of Hamiltonians deformed by conserved charges. For the spin-1/2 Heisenberg XXX chain we study a chiral Hamiltonian built from the scalar-chirality charge and total magnetization and solve it exactly by Bethe ansatz. Its ground state is a magnetized, current-carrying XXX eigenstate that breaks SU(2), time-reversal, and parity yet stays critical. This zero-entropy macrostate shows ballistic spin and chirality transport and admits realistic cold-atom and Rydberg platforms.

Wigner crystals are a paradigmatic form of interaction driven electronic order. A key open question is how Berry curvature and, more generally, quantum geometry reshape crystallization. The discovery of two-dimensional materials with relatively flat bands and pronounced Berry curvature has added fresh urgency to this question. Recent mean-field studies have proposed a topological variant of the Wigner crystal, the anomalous Hall crystal (AHC), with non-zero Chern number. However it remains unclear whether the AHC survives beyond the mean-field approximation. Here, we map out the ground-state phase diagram of the $\lambda$-jellium model - a simple model whose interaction strength and Berry curvature are independently tunable - using state-of-the-art neural-network variational Monte Carlo. The AHC is found to remain stable against quantum fluctuations. Surprisingly, quantum geometric effects are found to dramatically enhance crystallization. Both the AHC and the standard Wigner Crystal are stabilized at densities up to an order of magnitude above the critical density in the absence of quantum geometry, yet still significantly below the threshold predicted by mean-field theory. These striking results highlight the rich interplay between quantum fluctuations, quantum geometry, and crystallization, providing concrete guidance for experiments and enabling future explorations of fractionalized crystals and chiral superconductors.

Quantum geometric formulations of linear and nonlinear responses can be constructed from a single building block in the form of a gauge-invariant interband transition operator. Here, we identify a second building block for quantum geometry: a band-resolved adiabatic connection operator that captures the noncommutativity between band projectors and their momentum derivatives. The band-resolved adiabatic connection operator, first introduced in the theory of adiabatic driving, serves as a generalized angular momentum within the state manifold of single bands, and we employ it to reformulate expressions for the band-resolved orbital magnetic moment. This form provides a complementary geometric interpretation alongside the multiband separation between energetic- and quantum-state properties by the two-state Berry curvature. Our formalism allows us to present formulas valid for both nondegenerate and degenerate bands, thereby removing the limitations of the common Bloch-state formula. We illustrate our theory by calculating a large orbital magnetization emerging without spin-orbit coupling in a spin-compensated, noncoplanar anomalous Hall magnet with degenerate bands.

Long-lived spin-helix states facilitate the study of non-equilibrium dynamics in quantum magnets. We consider the decay of transverse spin-helices in antiferromagnetic spin-$S$ XXZ chains with single-ion anisostropy. The spin-helix decay is observable in the time evolution of the local magnetization that we calculate numerically for the system in the thermodynamic limit using infinite time-evolving block decimation simulations. Although the single-ion anisotropy prevents helix states from being eigenstates of the Hamiltonian, they still can be long-lived for appropriately chosen wave numbers. In case of an easy-axis exchange anisotropy the single-ion anisotropy may even stabilize the helices. Within a spin-wave approximation, we obtain a condition giving an estimate for the most stable wave number $Q$ that agrees qualitatively with our numerical results.

We propose an alternative to the infinite density-matrix renormalization approach for accessing quantum many-body states within a finite-size calculation that faithfully mimics the thermodynamic limit. Our method constructs environment matrix product operators (MPOs) representing the Hamiltonian of semi-infinite regions surrounding the target system. Starting from the finite-size ground-state MPS, we contract its Hamiltonian representation to generate effective environment MPOs, which are then attached to a renewed finite system in a recursive manner. This iterative embedding drives the system toward a bulk-like state with negligible finite-size effects. The scheme requires no assumption of homogeneity and achieves unprecedentedly long real-time dynamics free from boundary reflections.

Understanding superconductivity emerging from repulsive fermions remains a major challenge in condensed matter physics. In this paper, we investigate the pairing tendencies in a one-dimensional, three component repulsive Hubbard model, using the density matrix renormalization group method. At half-filling, the system exhibits density wave ground state due to strong Hubbard repulsions. Upon doping, we find that Cooper pairs can emerge, whose fluctuations predominate the long-range physics in the system across a wide parameter range. The effective attractions between Cooper pairs are mediated by the particle-hole fluctuations in the third non-pairing component, resembling an excitonic mechanism of superconductivity. The coexistence of multiple density waves and superconductivity at different fermion fillings is explored. We also present an analytical study of the pairing mechanism in both weak and strong coupling limits. Our results provide a new perspective for understanding and exploring unconventional superconductivities in strongly correlated fermionic systems.

We introduce a non-perturbative framework for quantizing chiral solitons in interacting quantum spin chains. This approach provides a direct lattice extension of the well-established $S$-duality between the sine-Gordon and Thirring models, thereby bridging the gap between continuum dualities and their lattice counterparts. By constructing the quantum chiral-soliton operators explicitly, we show how their unconventional dynamics appear in the excitation spectrum and correlation functions across the full Brillouin zone. A key result is that the dominant soliton tunneling amplitude alternates in sign, $\operatorname{sgn}(t_{1+}) = (-1)^{2S+1}$, sharply distinguishing half-odd-integer from integer spin chains. We further identify characteristic signatures of these chiral excitations in the dynamical spin structure factor, demonstrating their visibility in inelastic neutron scattering. Our results open a route to experimentally probing non-perturbative features of dual quantum field theories in condensed-matter settings.

Long-range moire patterns in twisted WSe2 enable a built-in, moire-length-scale ferroelectric polarization that can be directly harnessed in electronic devices. Such a built-in ferroic landscape offers a compelling means to enable ultralow-voltage and non-volatile electronic functionality in two-dimensional materials; however, achieving stable polarization control without charge trapping has remained a persistent challenge. Here, we demonstrate a moire-engineered ferroelectric field-effect transistor (FeFET) utilizing twisted WSe2 bilayers that leverages atomically clean van der Waals interfaces to achieve efficient polarization-channel coupling and trap-suppressed, ultralow-voltage operation (subthreshold swing of 64 mV per decade). The device exhibits a stable non-volatile memory window of 0.10 V and high mobility, exceeding the performance of previously reported two-dimensional FeFET and matching that of advanced silicon-based devices. In addition, capacitance-voltage spectroscopy, corroborated by self-consistent Landau-Ginzburg-Devonshire modeling, indicates ultrafast ferroelectric switching (~0.5 microseconds). These results establish moire-engineered ferroelectricity as a practical and scalable route toward ultraclean, low-power, and non-volatile 2D electronics, bridging atomistic lattice engineering with functional device architectures for next-generation memory and logic technologies.

This work presents the modeling of the magnetic 3d sublattice in mixed orthoferrites-orthochromites YFe1-xCrxO3 using classical Monte Carlo methods. It is shown that, when taking into account the competition of the Dzyaloshinskii vectors in the mixed compositions, magnetic moment compensations are observed, as well as angular magnetic configurations corresponding to the spin reorientation.

Two-dimensional (2D) Dirac fermions occur ubiquitously in condensed matter systems from topological phases to quantum critical points. Since the advent of topological semimetals, where the dispersion is often tilted around the band crossing where the Dirac fermion can appear, tilt has emerged as a key handle that controls physical properties. We study how tilt affects the transport and spectral properties of tilted 2D Dirac fermions under scalar disorder. Although our spectral analyses always show conformity to appropriate Gaussian ensembles, suggestive of delocalization, the conductivity scaling $g(L)$ shows a surprising richness. For a single Dirac node, relevant for quantum Hall transitions and topological insulator surface states, we find $g(L)\sim a_1\log(L)$ with a tilt-dependent coefficient a_1>0. Interestingly, when the tilt and transport directions are aligned, $a_1$ and hence $g(L)$ shows a spike at the critical point between the type-I and type-II regimes of the Dirac node. For systems with two Dirac nodes with unbroken time-reversal symmetry, pertinent to quasi-2D Dirac materials, we find $g(L)\sim L^{a_1}(\log L)^{a_2}$. However, we find a surprising tension between tilt along and perpendicular to the transport directions. For the former, $a_1$ changes sign as a function of tilt, hinting at a tilt-driven localization-delocalization transition, while a_1<0 for all tilts in the latter case, implying localization. These localized behaviors also reveal tension with the delocalization seen in spectral properties and suggest differing localization tendencies in real and Hilbert spaces. Overall, our work identifies tilt as an essential control parameter that uncovers rich and unconventional transport physics in 2D Dirac materials.

The interplay between superconductivity and charge-density wave (CDW) order, and its evolution with carrier density, is central to the physics of many quantum materials, notably high-$T_c$ cuprates and kagome metals. Hole-doped kagome compounds exhibit puzzling double-dome superconductivity and, as chemical substitution inevitably introduces quenched disorder, their properties remain poorly understood. Here, by leveraging the sensitivity of nuclear quadrupole resonance to local and static orderings, we uncover new features, primarily the incipient and fragmented CDW phases, in the charge landscape of CsV$_3$Sb$_{5-x}$Sn$_x$. Static CDW puddles are observed well above the transition temperature, a hallmark of pinning by defects. Their doping and temperature evolution indicate that, in the absence of disorder, the inverse Star-of-David $\pi$-shifted (ISD-$\pi$) CDW order would vanish near $x=0.12$, between the two superconducting domes. This critical doping represents a hidden quantum critical point. Nevertheless, the ISD-$\pi$ pattern persists well beyond previous reports, although its volume fraction is progressively reduced up to the critical doping at which it saturates. We establish that carrier doping promotes fragmentation of the ISD-$\pi$ order, whereas randomness preserves the ISD-$\pi$ patches.

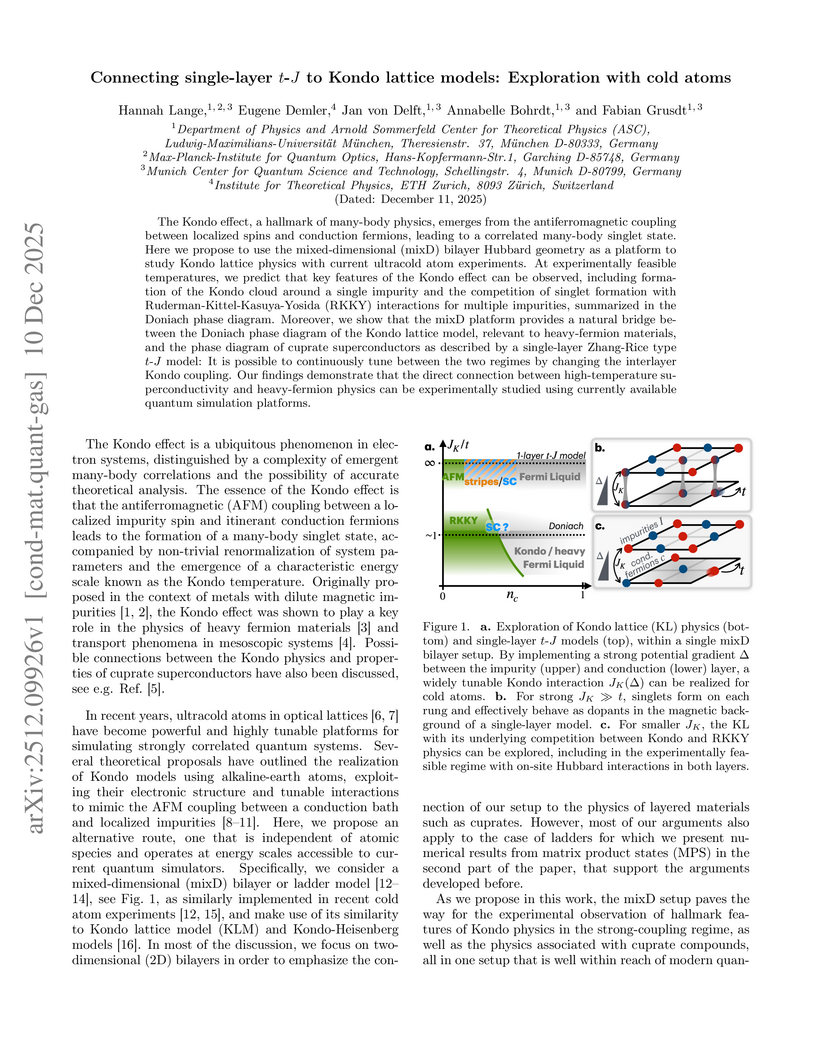
The Kondo effect, a hallmark of many-body physics, emerges from the antiferromagnetic coupling between localized spins and conduction fermions, leading to a correlated many-body singlet state. Here we propose to use the mixed-dimensional (mixD) bilayer Hubbard geometry as a platform to study Kondo lattice physics with current ultracold atom experiments. At experimentally feasible temperatures, we predict that key features of the Kondo effect can be observed, including formation of the Kondo cloud around a single impurity and the competition of singlet formation with Ruderman-Kittel-Kasuya-Yosida (RKKY) interactions for multiple impurities, summarized in the Doniach phase diagram. Moreover, we show that the mixD platform provides a natural bridge between the Doniach phase diagram of the Kondo lattice model, relevant to heavy-fermion materials, and the phase diagram of cuprate superconductors as described by a single-layer Zhang-Rice type $t$-$J$ model: It is possible to continuously tune between the two regimes by changing the interlayer Kondo coupling. Our findings demonstrate that the direct connection between high-temperature superconductivity and heavy-fermion physics can be experimentally studied using currently available quantum simulation platforms.

Motivated by recent angle-resolved photoemission spectroscopy (ARPES) experiments, we analyze the temperature, frequency, and momentum dependence of the single-particle scattering rate in a model of the $\gamma$-band of Sr$_2$RuO$_4$ under strain, with particular emphasis on the behavior near the Lifshitz transition where the Fermi energy crosses a single Van Hove point. While the scattering rate is only moderately anisotropic at zero strain, we find that it becomes strongly anisotropic at the Lifshitz point. At the lowest energies, we recover the expected universal behavior: the scattering rate varies (ignoring logarithmic corrections) as $\tau^{-1}\sim \omega$ at the Van Hove point and as $\tau^{-1}\sim \omega^{3/2}$ away from it. At higher energies, however, corrections of order $\omega^2$ become important in both regimes. We show that the experimentally observed behavior $\tau^{-1} \sim \omega^{\alpha}$ with $\alpha \approx 1.4(2)$ at the Van Hove point can be quantitatively explained by a superposition of linear and quadratic contributions to the scattering rate, which are comparable in magnitude at the intermediate energies probed by experiment, rather than in terms of a new universal power law. We further predict a distinctive anisotropy, strain dependence, and a non-monotonic frequency dependence of the scattering rate at a Lifshitz transition, all of which may be directly tested in experiments.