Due to entropic effects, it is possible that generic high-energy states of a quantum or classical system are ordered. This leads to spontaneous symmetry breaking at arbitrarily high temperatures. We present minimal models of entropic order that arise from very simple interactions. Our main examples are the Arithmetic Ising Model (AIM) and its quantum analogue, where usual Ising spins are replaced by non-negative integers. Using a large-flavor expansion together with numerical simulations, we find that the high-temperature phase is ordered in the classical and quantum models. We also introduce classical gas models whose interactions drive the system to a crystal at high temperatures.

Relaxation processes in topological phases such as quantum spin liquids are controlled by the dynamics and interaction of fractionalized excitations. In layered materials hosting two-dimensional topological phases, elementary quasiparticles can diffuse freely within the layer, whereas only pairs (or more) can hop between layers - a fundamental consequence of topological order. Using exact solutions of emergent nonlinear diffusion equations and particle-based stochastic simulations, we explore how pump-probe experiments can provide unique signatures of the presence of $2d$ topological excitations in a $3d$ material. Here we show that the characteristic time scale of such experiments is inversely proportional to the initial excitation density, set by the pump intensity. A uniform excitation density created on the surface of a sample spreads subdiffusively into the bulk with a mean depth $\bar z$ scaling as $\sim t^{1/3}$ when annihilation processes are absent. The propagation becomes logarithmic, $\bar z \sim \log t$, when pair-annihilation is allowed. Furthermore, pair-diffusion between layers leads to a new decay law for the total density, $n(t) \sim (\log^2 t)/t$ - slower than in a purely $2d$ system. We discuss possible experimental implications for pump-probe experiments in samples of finite width.

Virtually every biological rate changes with temperature, but the mechanisms underlying these responses differ between different processes. Here, we bring together the main theoretical approaches used to describe temperature-rate relationships, ranging from empirical curve shapes to reaction-level kinetics and network-based dynamical frameworks. These models highlight how temperature influences not only the speed of elementary reactions, but also the behavior that emerges when many reactions interact through regulation, feedback, or stochastic transitions. By outlining the assumptions and implications of each perspective, we aim to clarify how different modeling strategies connect molecular processes to physiological temperature response curves and to point toward integrative frameworks that can better explain the diversity of biological thermal responses.

The importance of molecular-scale forces in sculpting biological form and function has been acknowledged for more than a century. Accounting for forces in biology is a problem that lies at the intersection of soft condensed matter physics, statistical mechanics, computer simulations and novel experimental methodologies, all adapted to a cellular context. This review surveys how forces arise within the cell. We provide a summary of the relevant background in basic biophysics, of soft-matter systems in and out of thermodynamic equilibrium, and of various force measurement methods in biology. We then show how these ideas can be incorporated into a description of cell-scale processes where forces are involved. Our examples include polymerization forces, motion of molecular motors, the properties of the actomyosin cortex, the mechanics of cell division, and shape changes in tissues. We show how new conceptual frameworks are required for understanding the consequences of cell-scale forces for biological function. We emphasize active matter descriptions, methodological tools that provide ways of incorporating non-equilibrium effects in a systematic manner into conceptual as well as quantitative descriptions. Understanding the functions of cells will necessarily require integrating the role of physical forces with the assimilation and processing of information. This integration is likely to have been a significant driver of evolutionary change.

We propose a protocol to construct atypical high-energy eigenstates in quantum systems by using ground states of Hamiltonians deformed by conserved charges. For the spin-1/2 Heisenberg XXX chain we study a chiral Hamiltonian built from the scalar-chirality charge and total magnetization and solve it exactly by Bethe ansatz. Its ground state is a magnetized, current-carrying XXX eigenstate that breaks SU(2), time-reversal, and parity yet stays critical. This zero-entropy macrostate shows ballistic spin and chirality transport and admits realistic cold-atom and Rydberg platforms.

Insomuch as statistical mechanics circumvents the formidable task of addressing many-body dynamics, it remains a challenge to derive macroscopic properties from a solution to Hamiltonian equations for microscopic motion of an isolated system. Launching new attacks on this long-standing problem -- part of Hilbert's sixth problem -- is urgently important, for focus of statistical phenomena is shifting from a fictitious ensemble to an individual member, i.e. a mechanically isolated system. Here we uncover a common probabilistic structure, the concentration of measure, in Hamiltonian dynamics of two families of systems, the Fermi-Pasta-Ulam-Tsingou (FPUT) model which is finite-dimensional and (almost) ergodic, and the Gross-Pitaevskii equation (GPE) which is infinite-dimensional and suffers strong ergodicity breaking. That structure is protected by the geometry of phase space and immune to ergodicity breaking, leading to counterintuitive phenomena. Notably, an isolated FPUT behaves as a thermal ideal gas even for strong modal interaction, with the thermalization time analogous to the Ehrenfest time in quantum chaos, while an isolated GPE system, without any quantum inputs, escapes the celebrated ultraviolet catastrophe through nonlinear wave localization in the mode space, and the Rayleigh-Jeans equilibrium sets in the localization volume. Our findings may have applications in nonlinear optics and cold-atom dynamics.

The second-order phase transitions in the Ising model and liquid-gas systems share a universality class and critical exponents, despite the absence of $Z_2$ symmetry in the liquid-gas Hamiltonian. This discrepancy highlights a central puzzle in critical phenomena: what is the influence of asymmetry on scaling laws? For over a century, this question has been explored through examining violations of the empirical ``rectilinear diameter law'' for the subcritical coexistence curve, where asymmetry could generate singular corrections. Here, we extend this investigation to the supercritical regime. We propose a supercritical-subcritical correspondence, drawing a formal analogy between the subcritical coexistence curve and recently defined supercritical boundary lines ($L^\pm$ lines). Our theory predicts that the linear mixing of physical fields - a hallmark of asymmetric systems - produces universal scaling corrections, with antisymmetric coefficients, in these supercritical loci. We verify these predictions using liquid-gas data from the NIST database and a model liquid-liquid transition. Furthermore, we demonstrate that the same asymmetric scaling framework governs the behavior of higher-order cumulants in the order parameter distribution.

Active systems across scales, ranging from molecular machines to human crowds, are usually modeled as assemblies of self-propelled particles driven by internally generated forces. However, these models often assume memoryless dynamics and no coupling of internal active forces to the environment. Here, guided by the example of living cells, which have recently been shown to display multi-timescale memory effects, we introduce a general theoretical framework that goes beyond this paradigm by incorporating internal state dynamics and environmental sensing into active particle models. We show that when the self-propulsion of an agent depends on internal variables with their own complex dynamics - modulated by local environmental cues - environmental memory spontaneously emerges and gives rise to new classes of behaviours. These include memory-induced responses, adaptable localization in complex landscapes, suppression of motility-induced phase separation, and enhanced jamming transitions. Our results demonstrate how minimal information processing capabilities, intrinsic to non-equilibrium agents with internal states like living cells, can profoundly influence both individual and collective behaviours. This framework bridges cell-scale activity and large-scale intelligent motion in cell assemblies, and opens the way to the quantitative analysis and design of systems ranging from synthetic colloids to biological collectives and robotic swarms.

Witnessing and tracking topological phase transitions induced by interactions with the environment is a crucial challenge. Among the various experimental approaches to detect topological properties, the Mean Chiral Displacement (MCD) has emerged as a powerful bulk probe in one-dimensional chiral systems, allowing the extraction of the topological invariant from single-particle dynamics. Here we study the dynamics of a single particle in a one-dimensional Su-Schrieffer-Heeger chain coupled to multiple cavity modes via inter-cell hopping terms, focusing on the out-of-equilibrium behavior of the MCD. We show that, whenever the frequency is larger than the static hopping amplitudes, the coupling induces a discontinuous jump in the MCD, already at small times, signaling that such a coupling also leaves a signature in the survival edge probability when the dynamics are initialized at one of the two edges. For frequencies comparable to the static hopping amplitudes, topological order competes with dissipative effects, which makes the MCD behave smoothly, retaining information about the driven-dissipative topology.

Phase separation in confined environments is a fundamental process underlying geological flows, porous filtration, emulsions, and intracellular organization. Yet, how confinement and activity jointly govern coarsening kinetics and interfacial morphology remains poorly understood. Here, we use large-scale molecular dynamics simulations to investigate vapor-liquid phase separation of passive and active fluids embedded in complex porous media. By generating porous host structures via a freeze-quench protocol, we systematically control the average pore size and demonstrate that confinement induces a crossover from the Lifshitz-Slyozov power-law growth to logarithmically slowed coarsening, ultimately arresting domain evolution. Analysis of correlation functions and structure factors reveals that confined passive systems exhibit fractal interfaces, violating Porod's law and indicating rough morphological arrest. In contrast, introducing self-propulsion dramatically changes the coarsening pathway: activity restores smooth interfaces, breaks the confinement-induced scaling laws, and drives a transition from logarithmic to ballistic domain growth at high activity levels. Our findings reveal an activity-controlled mechanism to overcome geometric restrictions and unlock coarsening in structurally heterogeneous environments. These insights establish a unifying framework for nonequilibrium phase transitions in porous settings, with broad relevance to active colloids, catalytic media, and biologically crowded systems, where living matter routinely reorganizes within geometric constraints to sustain function.

We explore the influence of geometry in the critical behavior of sparse long-range spin models. We examine a model with interactions that can be continuously tuned to induce distinct changes in the metric, topology, and dimensionality of the coupling graph. This underlying geometry acts as the driver of criticality, with structural changes in the graph coinciding with and dictating the phase boundaries. We further discuss how this framework connects naturally to realizations in tweezer arrays with Rydberg excitations. In certain cases, the effective geometry can be incorporated in the layout of atoms in tweezers to realize phase transitions that preserve universal features, simplifying their implementation in near-term experiments.

A large family of multispin interacting one-dimensional quantum spin models with $Z(N)$ symmetry and a free-particle eigenspectra are known in the literature. They are free-fermionic ($N=2$) and free-parafermionic ($N\geq 2$) quantum chains. The essential ingredient that implies the free-particle spectra is the fact that these Hamiltonians are expressed in terms of generators of a $Z(N)$ exchange algebra. In all these known quantum chains the number of spins in all the multispin interactions (range of interactions) is the same and therefore, the models have homogeneous interacting range. In this paper we extend the $Z(N)$ exchange algebra, by introducing new models with a free-particle spectra, where the interaction ranges of the multispin interactions are not uniform anymore and depends on the lattice sites (non-homogeneous interacting range). We obtain the general conditions that the site-dependent ranges of the multispin interactions have to satisfy to ensure a free-particle spectra. Several simple examples are introduced. We study in detail the critical properties in the case where the range of interactions of the even (odd) sites are constant. The dynamical critical exponent is evaluated in several cases.

The potential of mean force (PMF) is an effective average potential acting on an open system, renormalized due to the interaction with the surrounding thermal bath. The PMF is defined for an equilibrium ensemble, and generally it is not clear how to use it when the system is out of equilibrium and described by a (generalized) Langevin equation. We study a model where the system is a single particle (so there are no complications related to internal forces) and a non-trivial PMF is due to the presence of on-site (anchor) potentials applied to the bath particles. We found that the PMF does not merely replace the external potential, but also makes the dissipation kernel and statistical properties of noise dependent on the system's position. That dependence is determined by the internal bath and system-bath interactions and is a priori unknown. Therefore, in the general case the Langevin equation with the PMF is not closed and thus inoperable. However, for systems with linear forces the aforementioned dependence on the system's position may be canceled. As an example, we consider a model where the bath is formed by the Klein-Gordon chain, i. e. a harmonic chain with on-site harmonic potentials. In that case, the generalized Langevin equation has the standard form with an external potential replaced by a quadratic PMF.

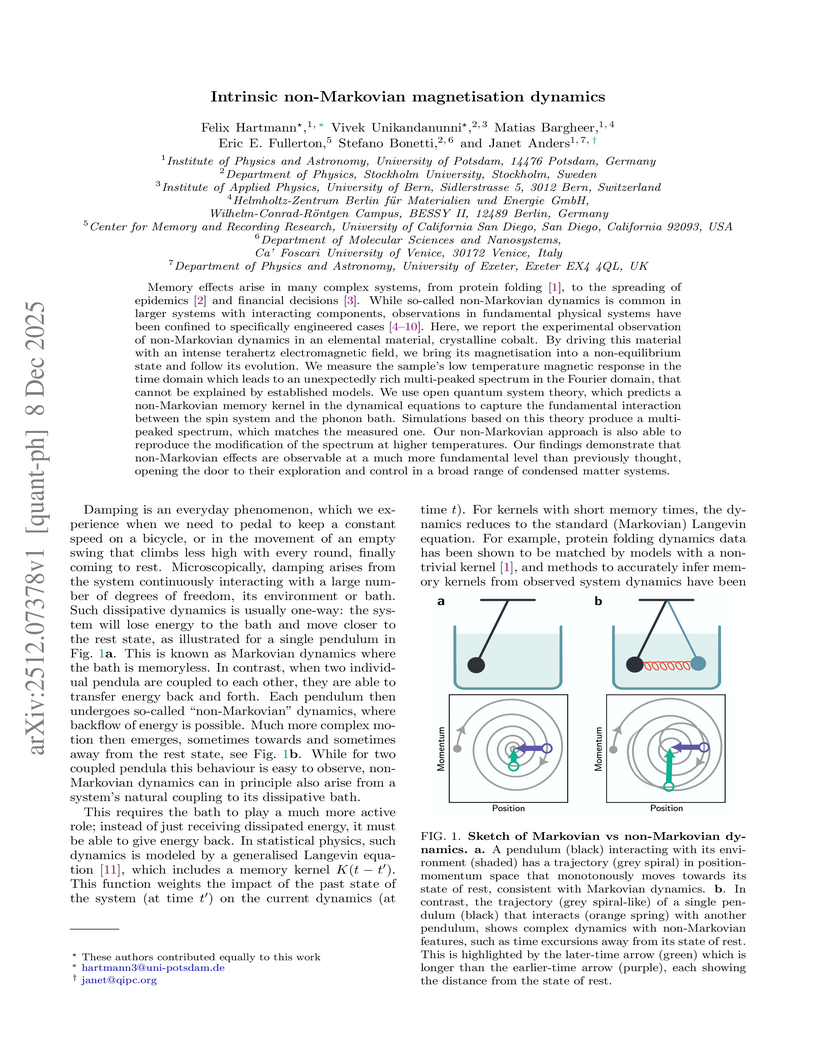
Memory effects arise in many complex systems, from protein folding, to the spreading of epidemics and financial decisions. While so-called non-Markovian dynamics is common in larger systems with interacting components, observations in fundamental physical systems have been confined to specifically engineered cases. Here, we report the experimental observation of non-Markovian dynamics in an elemental material, crystalline cobalt. By driving this material with an intense terahertz electromagnetic field, we bring its magnetisation into a non-equilibrium state and follow its evolution. We measure the sample's low temperature magnetic response in the time domain which leads to an unexpectedly rich multi-peaked spectrum in the Fourier domain, that cannot be explained by established models. We use open quantum system theory, which predicts a non-Markovian memory kernel in the dynamical equations to capture the fundamental interaction between the spin system and the phonon bath. Simulations based on this theory produce a multi-peaked spectrum, which matches the measured one. Our non-Markovian approach is also able to reproduce the modification of the spectrum at higher temperatures. Our findings demonstrate that non-Markovian effects are observable at a much more fundamental level than previously thought, opening the door to their exploration and control in a broad range of condensed matter systems.

Reliably simulating two-dimensional many-body quantum dynamics with projected entangled pair states (PEPS) has long been a difficult challenge. In this work, we overcome this barrier for low-energy quantum dynamics by developing a stable and efficient time-dependent variational Monte Carlo (tVMC) framework for PEPS. By analytically removing all gauge redundancies of the PEPS manifold and exploiting tensor locality, we obtain a numerically well-conditioned stochastic reconfiguration (SR) equation amenable to robust solution using the efficient Cholesky decomposition, enabling long-time evolution in previously inaccessible regimes. We demonstrate the power and generality of the method through four representative real-time problems in two dimensions: (I) chiral edge propagation in a free-fermion Chern insulator; (II) fractionalized charge transport in a fractional Chern insulator; (III) vison confinement dynamics in the Higgs phase of a Z2 lattice gauge theory; and (IV) superfluidity and critical velocity in interacting bosons. All simulations are performed on 12x12 or 13x13 lattices with evolution times T = 10 to 12 using modest computational resources (1 to 5 days on a single GPU card). Where exact benchmarks exist (case I), PEPS-tVMC matches free-fermion dynamics with high accuracy up to T = 12. These results establish PEPS-tVMC as a practical and versatile tool for real-time quantum dynamics in two dimensions. The method extends the reach of classical tensor-network simulations for studying elementary excitations in quantum many-body systems and provides a valuable computational counterpart to emerging quantum simulators.

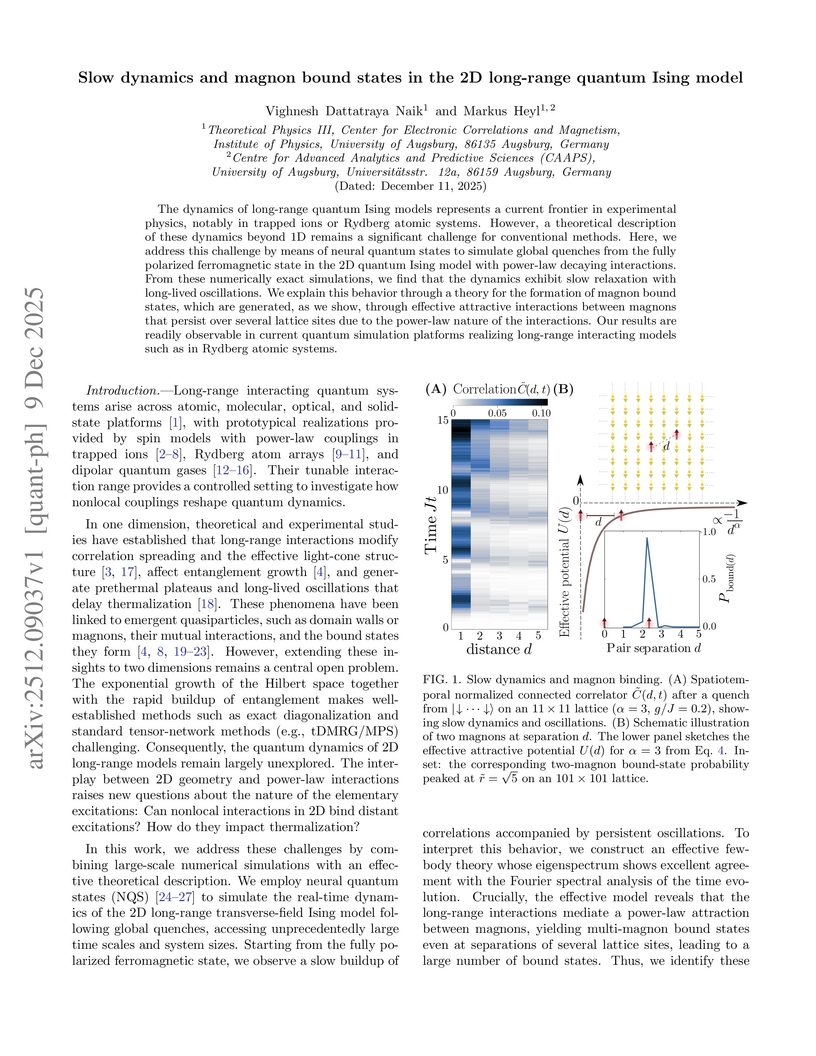
The dynamics of long-range quantum Ising models represents a current frontier in experimental physics, notably in trapped ions or Rydberg atomic systems. However, a theoretical description of these dynamics beyond 1D remains a significant challenge for conventional methods. Here, we address this challenge by means of neural quantum states to simulate global quenches from the fully polarized ferromagnetic state in the 2D quantum Ising model with power-law decaying interactions. From these numerically exact simulations, we find that the dynamics exhibit slow relaxation with long-lived oscillations. We explain this behavior through a theory for the formation of magnon bound states, which are generated, as we show, through effective attractive interactions between magnons that persist over several lattice sites due to the power-law nature of the interactions. Our results are readily observable in current quantum simulation platforms realizing long-range interacting models such as in Rydberg atomic systems.

We investigate thermalization and time-dependent Bose-Einstein condensate formation in ultracold Dy-164 using a nonlinear boson diffusion equation. As compared to alkali atoms such as K-39 or Rb-87, the strong magnetic dipole interaction modifies the scattering-length dependence of the transport coefficients that govern thermalization and condensate formation. A prediction for the time-dependent condensate fraction in Dy-164 is made.

Self-propelled particles accumulate on repulsive barriers in so-called active wetting, but the relationship between this process and equilibrium wetting remains unclear. Using an exact (noiseless) hydrodynamic framework for an active lattice gas, we show, using a slit geometry with periodic boundary conditions, that active matter exhibits both fully- and partially-wet states, with a critical wetting transition between them. Furthermore, we demonstrate the existence of a spontaneous-symmetry-breaking ratchet current in the partially wet state, leading to departure of the bulk densities from their binodal values and the emergence of a novel dynamical pathway for the full-to-partial wetting transition. We elucidate this modified dynamical pathway using a minimal model. The results, while establishing a direct connection between active and equilibrium wetting, also identify the nonequilibrium consequences of activity.

We demonstrate that if a quantum Markovian semigroup satisfies the standard quantum detailed balance condition, its generator admits a special representation that yields a vanishing entropy production rate. Conversely, if the generator admits a special representation adhering to the condition of thermodynamic consistency and leading to a vanishing entropy production rate, then the corresponding quantum Markovian semigroup must satisfy the standard quantum detailed balance condition. In this context, we adopt the definition of entropy production rate that is motivated by the physics literature and standard for thermodynamically consistent Lindbladians.