Periodically driven coherent conductors provide a universal platform for the development of quantum transport devices. Here, we lay down a comprehensive theory to describe the thermodynamics of these systems. We first focus on moderate thermo-electrical biases and low driving frequencies. For this linear response regime, we establish generalized Onsager-Casimir relations and an extended fluctuation-dissipation theorem. Furthermore, we derive a family of thermodynamic bounds proving that any local matter or heat current puts a non-trivial lower limit on the overall dissipation rate of a coherent transport process. These bounds do not depend on system-specific parameters, are robust against dephasing and involve only experimentally accessible quantities. They thus provide powerful tools to optimize the performance of mesoscopic devices and for thermodynamic inference, as we demonstrate by working out three specific applications. We then show that physically transparent extensions of our bounds hold also for strong biases and high frequencies. These generalized bounds imply a thermodynamic uncertainty relation that fully accounts for quantum effects and periodic driving. Moreover, they lead to a universal and operationally accessible bound on entropy production that can be readily used for thermodynamic inference and device engineering far from equilibrium. Connecting a broad variety of topics that range from thermodynamic geometry over thermodynamic uncertainty relations to quantum engineering, our work provides a unifying thermodynamic theory of coherent transport that can be tested and utilized with current technologies.

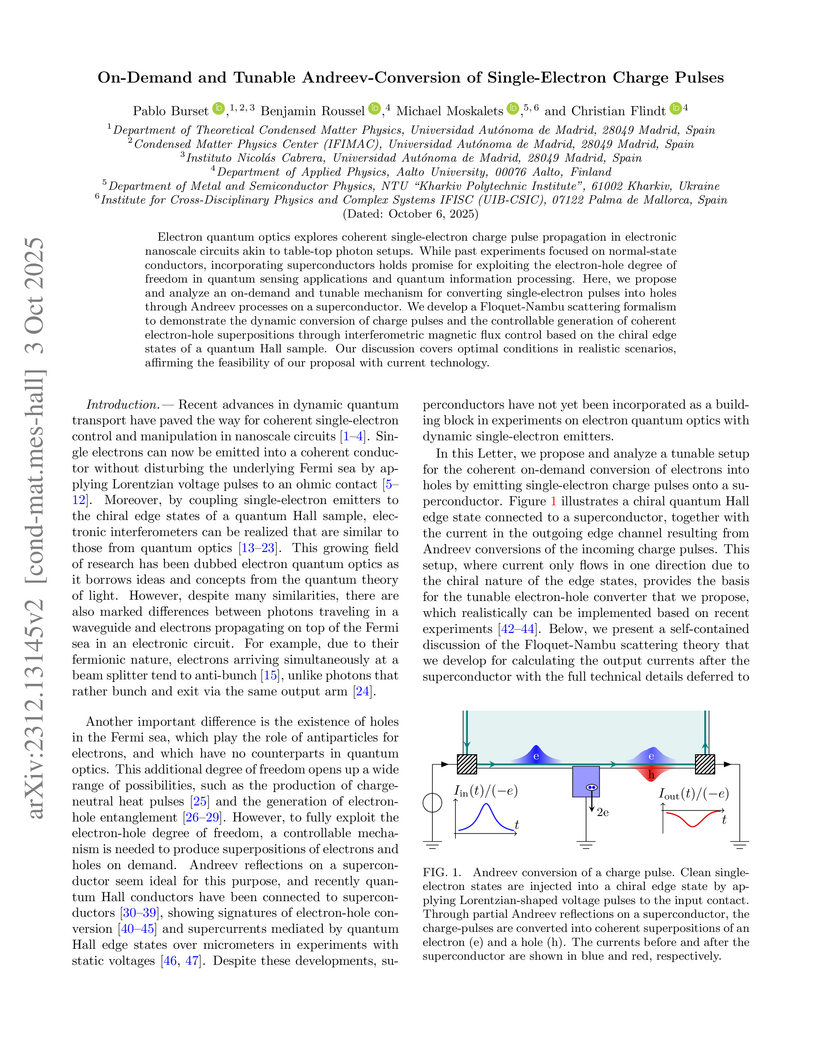
Electron quantum optics explores coherent single-electron charge pulse propagation in electronic nanoscale circuits akin to table-top photon setups. While past experiments focused on normal-state conductors, incorporating superconductors holds promise for exploiting the electron-hole degree of freedom in quantum sensing applications and quantum information processing. Here, we propose and analyze an on-demand and tunable mechanism for converting single-electron pulses into holes through Andreev processes on a superconductor. We develop a Floquet-Nambu scattering formalism to demonstrate the dynamic conversion of charge pulses and the controllable generation of coherent electron-hole superpositions through interferometric magnetic flux control based on the chiral edge states of a quantum Hall sample. Our discussion covers optimal conditions in realistic scenarios, affirming the feasibility of our proposal with current technology.

Kinetic Uncertainty Relations (KURs) establish quantum transport precision limits by linking signal-to-noise ratio (SNR) to the system's dynamical activity, valid in the weak-coupling regime where particle-like transport dominates. At strong coupling, quantum coherence challenges the validity of KURs and questions the concept of activity itself. In this Letter, we achieve two distinct, yet complementary main results. First, we introduce a general definition of dynamical activity valid at arbitrary coupling, which reveals the breakdown of standard KURs at strong coupling. Second, we prove a novel uncertainty relation valid at arbitrary coupling strength, which we denote Quantum KUR (QKUR). This QKUR corresponds to a nontrivial quantum extension of KUR, involving fundamental contributions of the generalized dynamical activity. These two achievements provide a general framework for out-of-equilibrium quantum transport precision analysis, in close analogy with the transition from TURs to QTURs [Phys. Rev. Lett. 135, 046302]. Explicit steady-state expressions are obtained within Green's-function and Landauer-Büttiker formalisms. We illustrate these concepts for paradigmatic quantum-coherent mesoscopic devices: a single quantum channel pinched by a quantum point contact and open single- and double-quantum dot systems.

Recent progress in experimental techniques such as single particle tracking allows to analyze both nonequilibrium properties and approach to equilibrium. There are examples showing that processes occurring at finite timescales are distinctly different than their equilibrium counterparts. In this work we analyze a similar problem of approach to nonequilibrium. We consider an archetypal model of nonequilibrium system consisting of a Brownian particle dwelling in a spatially periodic potential and driven by an external time-periodic force. We focus on a diffusion process and monitor its development in time. In the presented parameter regime the excess kurtosis measuring the Gaussianity of the particle displacement distribution evolves in a non-monotonic way: first it is negative (platykurtic form), next it becomes positive (leptokurtic form) and then decays to zero (mesokurtic form). Despite the latter fact diffusion in the long time limit is Brownian, yet non-Gaussian. Moreover, we discover a correlation between non-Gaussianity of the particle displacement distribution and transient anomalous diffusion behavior emerging for finite timescales.

We present a comprehensive Floquet-Nambu theory to describe the time-dependent quantum transport in mesoscopic circuits involving superconductors. The central object of our framework is the first-order correlation function, which accounts for the excitations that are generated by a time-dependent voltage and their coherent scattering off the interface with a superconductor. We analyze the time-dependent current generated by periodic voltage pulses and how it depends on the excitation energies of the voltage drive compared to the gap of the superconductor. Our formalism allows us to identify the conditions for the excitations that are scattered off the superconductor to become coherent electron-hole superpositions. To this end, we consider the purity of the outgoing states, which characterizes their ability to carry quantum information. Our framework paves the way for systematic investigations of time-dependent scattering problems involving superconductivity, and it may help interpret future experiments in electron quantum optics with superconductors.

Diffusion coefficient usually decreases when friction increases. We analyze the opposite behavior in the paradigmatic system consisting of an inertial Brownian particle moving in a symmetric spatially periodic potential and driven by an unbiased time periodic force. For tailored parameter set in strong dissipation regime the particle spreading can be giantly amplified: if the friction is twice as large then the diffusion grows up to five orders of magnitude. The mechanism lying behind this effect is related to bifurcation of periodic orbits oscillating around the potential maximum and their symmetric displacement towards the adjacent potential minima when the friction coefficient increases. On the other hand, in the weak dissipation regime, where the increase of diffusion vs friction is also observed, the effect is induced by a non-monotonic change of population of the running orbits. However, in this regime the enhancement of diffusion is much smaller.

Based on the calculation and analysis of local Green functions of impurity atoms of low concentration in a two-dimensional graphene lattice, the conditions for the formation and characteristics of local discrete levels with energies lying outside the band of the quasi-continuous spectrum and quasi-localized states with energies near the Fermi one are determined. Specific calculations were performed for boron and nitrogen impurity atoms, which can actually replace carbon in graphite and graphene nanostructures. For a boron impurity that forms local discrete levels outside the band of the quasi-continuous spectrum, sufficiently simple analytical expressions for the conditions for their formation, energy, intensity at the impurity atom, and damping parameter are obtained. An analysis of the formation of states quasi-localized on nitrogen impurities with energy near the Fermi level in graphene nanostructures was carried out.

We study stochastic resonance in molecular junctions driven by a periodically-varying external field. This is done using the time-dependent Landauer-B{ü}ttiker formalism, which follows from exact analytical solutions to the Kadanoff-Baym equations describing the molecular junction subject to an arbitrary time-dependent bias. We focus on a double quantum dot nanojunction and compare the effects of the temperature with the fluctuating bias in the statically-driven case. We then consider the combined effect of AC-driving and white noise fluctuations on the rectified current through the nanojunction, and find a stochastic resonance effect, where at certain driving conditions the bias fluctuations enhance the current signal. The study is then extended to include the color noise in the applied bias, so that the combined effect of the color noise correlation time and driving frequency on stochastic resonance is investigated. We thereby demonstrate that photon-assisted transport can be optimized by a suitably tuned environment.