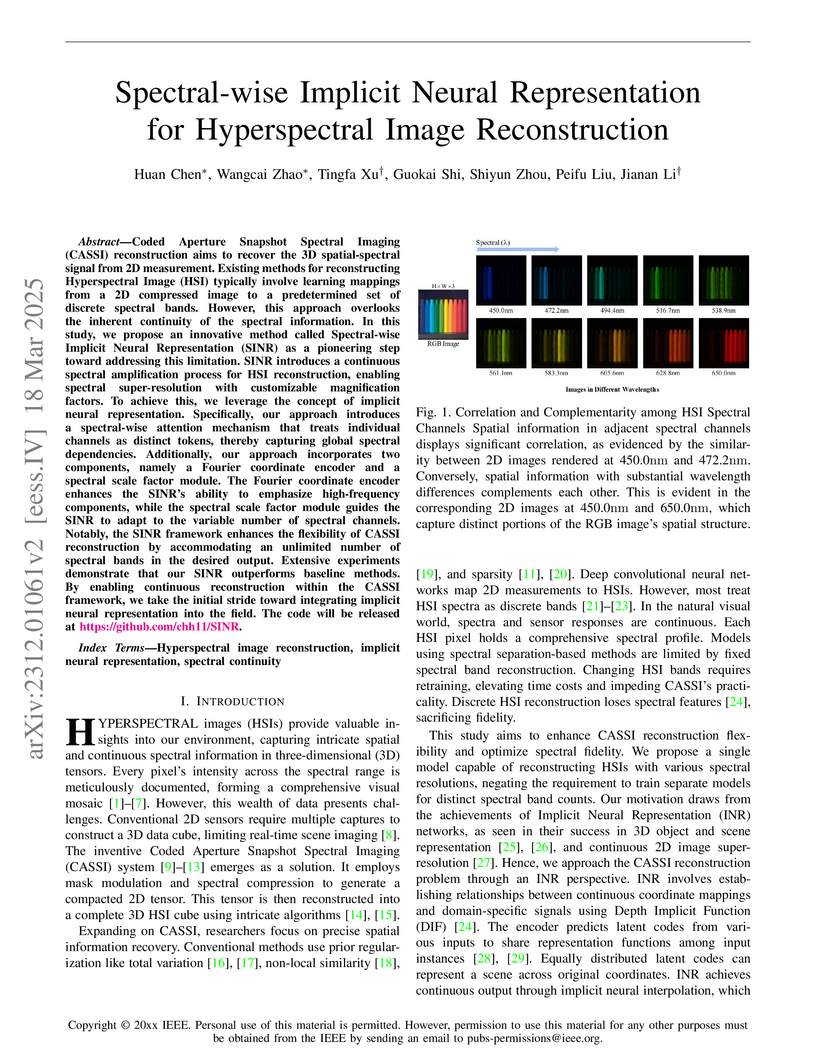
Coded Aperture Snapshot Spectral Imaging (CASSI) reconstruction aims to recover the 3D spatial-spectral signal from 2D measurement. Existing methods for reconstructing Hyperspectral Image (HSI) typically involve learning mappings from a 2D compressed image to a predetermined set of discrete spectral bands. However, this approach overlooks the inherent continuity of the spectral information. In this study, we propose an innovative method called Spectral-wise Implicit Neural Representation (SINR) as a pioneering step toward addressing this limitation. SINR introduces a continuous spectral amplification process for HSI reconstruction, enabling spectral super-resolution with customizable magnification factors. To achieve this, we leverage the concept of implicit neural representation. Specifically, our approach introduces a spectral-wise attention mechanism that treats individual channels as distinct tokens, thereby capturing global spectral dependencies. Additionally, our approach incorporates two components, namely a Fourier coordinate encoder and a spectral scale factor module. The Fourier coordinate encoder enhances the SINR's ability to emphasize high-frequency components, while the spectral scale factor module guides the SINR to adapt to the variable number of spectral channels. Notably, the SINR framework enhances the flexibility of CASSI reconstruction by accommodating an unlimited number of spectral bands in the desired output. Extensive experiments demonstrate that our SINR outperforms baseline methods. By enabling continuous reconstruction within the CASSI framework, we take the initial stride toward integrating implicit neural representation into the field.

Surface integral equations (SIEs)-based boundary element methods are widely used for analyzing electromagnetic scattering scenarii. However, after discretization of SIEs, the spectrum and eigenvectors of the boundary element matrices are not usually representative of the spectrum and eigenfunctions of the underlying surface integral operators, which can be problematic for methods that rely heavily on spectral properties. To address this issue, we delineate some efficient algorithms that allow for the computation of matrix square roots and inverse square roots of the Gram matrices corresponding to the discretization scheme, which can be used for revealing the spectrum of standard electromagnetic integral operators. The algorithms, which are based on properly chosen expansions of the square root and inverse square root functions, are quite effective when applied to several of the most relevant Gram matrices used for boundary element discretizations in electromagnetics. Tables containing different sets of expansion coefficients are provided along with comparative numerical experiments that evidence advantages and disadvantages of the different approaches. In addition, to demonstrate the spectrum-revealing properties of the proposed techniques, they are applied to the discretization of the problem of scattering by a sphere for which the analytic spectrum is known.

Hyperspectral salient object detection (HSOD) aims to extract targets or regions with significantly different spectra from hyperspectral images. While existing deep learning-based methods can achieve good detection results, they generally necessitate pixel-level annotations, which are notably challenging to acquire for hyperspectral images. To address this issue, we introduce point supervision into HSOD, and incorporate Spectral Saliency, derived from conventional HSOD methods, as a pivotal spectral representation within the framework. This integration leads to the development of a novel Spectrum-oriented Point-supervised Saliency Detector (SPSD). Specifically, we propose a novel pipeline, specifically designed for HSIs, to generate pseudo-labels, effectively mitigating the performance decline associated with point supervision strategy. Additionally, Spectral Saliency is employed to counteract information loss during model supervision and saliency refinement, thereby maintaining the structural integrity and edge accuracy of the detected objects. Furthermore, we introduce a Spectrum-transformed Spatial Gate to focus more precisely on salient regions while reducing feature redundancy. We have carried out comprehensive experiments on both HSOD-BIT and HS-SOD datasets to validate the efficacy of our proposed method, using mean absolute error (MAE), E-measure, F-measure, Area Under Curve, and Cross Correlation as evaluation metrics. For instance, on the HSOD-BIT dataset, our SPSD achieves a MAE of 0.031 and an F-measure of 0.878. Thorough ablation studies have substantiated the effectiveness of each individual module and provided insights into the model's working mechanism. Further evaluations on RGB-thermal salient object detection datasets highlight the versatility of our approach.