We theoretically investigate thermodynamic properties in a quasi-one-dimensional single-component dipolar Fermi gas at finite temperatures. The self-bound fermionic droplet can be achieved by exchange correlations with the long-range dipole-dipole interactions under the quasi-one-dimensional confinement, where the interaction can be tuned by tilting the dipoles along the system coordinate. Using the Hartree-Fock approximation, we show how the liquid-gas phase transition occurs in this system, and elucidate the finite-temperature phase structure consisting of the gas phase, liquid phase, their coexistence, and the spinodal phase. We also discuss its similarity with the liquid-gas phase transition in nuclear matter through the comparison with phenomenological models. Our results would be useful for an interdisciplinary understanding of self-bound fermionic matter as well as an analog quantum simulation of nuclear systems.

We investigate the critical temperature of a relativistic Bose-Einstein condensate of charged bosons driven by rotation in a parallel magnetic field [Y. Liu and I. Zahed, Phys. Rev. Lett. {\bf120}, 032001 (2018)]. For non-interacting bosons, the critical temperature can only be determined for a system with fixed angular momentum. We find that the critical temperature of the non-interacting system vanishes due to the fact that the system is quasi-one-dimensional, indicating that non-interacting bosons cannot undergo Bose-Einstein condensation. For interacting bosons, we investigate a system with quartic self-interaction. We show that the order parameter vanishes and the off-diagonal long-range order is absent at any nonzero temperature because of the quasi-one-dimensional feature, in accordance with the Coleman-Mermin-Wagner-Hohenberg theorem.

We demonstrate deterministic preparation of arbitrary two-component product states of fermionic $^6$Li atoms in an 8$\times$8 optical tweezer array, achieving motional ground-state fidelities above 98.5\%. Leveraging the large differential magnetic moments for spin-resolution, with parallelized site- and number-resolved control, our approach addresses key challenges for low-entropy quantum state engineering. Combined with high-fidelity spin-, site-, and density-resolved readout within a single \qty{20}{\us} exposure, and \qty{3}{\s} experimental cycles, these advances establish a fast, scalable, and programmable architecture for fermionic quantum simulation.

We investigate a variational Monte Carlo framework for trapped one-dimensional mixture of spin-$\frac{1}{2}$ fermions using Kolmogorov-Arnold networks (KANs) to construct universal neural-network wavefunction ansätze. The method can, in principle, achieve arbitrary accuracy, limited only by the Monte Carlo sampling and was checked against exact results at sub-percent precision. For attractive interactions, it captures pairing effects, and in the impurity case it agrees with known results. We present a method of systematic transfer learning in the number of network parameters, allowing for efficient training for a target precision. We vastly increase the efficiency of the method by incorporating the short-distance behavior of the wavefunction into the ansätz without biasing the method.

Scalability remains a major challenge in building practical fault-tolerant quantum computers. Currently, the largest number of qubits achieved across leading quantum platforms ranges from hundreds to thousands. In atom arrays, scalability is primarily constrained by the capacity to generate large numbers of optical tweezers, and conventional techniques using acousto-optic deflectors or spatial light modulators struggle to produce arrays much beyond $\sim 10,000$ tweezers. Moreover, these methods require additional microscope objectives to focus the light into micrometer-sized spots, which further complicates system integration and scalability. Here, we demonstrate the experimental generation of an optical tweezer array containing $280\times 280$ spots using a metasurface, nearly an order of magnitude more than most existing systems. The metasurface leverages a large number of subwavelength phase-control pixels to engineer the wavefront of the incident light, enabling both large-scale tweezer generation and direct focusing into micron-scale spots without the need for a microscope. This result shifts the scalability bottleneck for atom arrays from the tweezer generation hardware to the available laser power. Furthermore, the array shows excellent intensity uniformity exceeding $90\%$, making it suitable for homogeneous single-atom loading and paving the way for trapping arrays of more than $10,000$ atoms in the near future.

Supersolidity, combining superfluid and crystalline orders, has been realized in dipolar Bose-Einstein condensates by tuning interatomic interactions. Here we show that supersolidity can also emerge from mode coupling at a superfluid-solid interface, without modifying bulk interactions and for a broad class of superfluids. Using an analytical and numerical treatment of the coupled superfluid and phonon fields, we derive the criterion for a density-modulation instability driven by interfacial coupling and dependent on dimensionality. In superfluid helium, the instability first appears at the roton mode, while in a Bose-Einstein condensate with contact interactions it occurs at the lowest accessible wave vector set by the system size. Beyond the threshold, the ground state acquires an interfacial density modulation while the bulk remains superfluid, forming a hybrid superfluid-supersolid phase. Our results identify interfacial mode coupling as a promising route to supersolidity, enabling the simultaneous exploitation of interfacial supersolid and bulk superfluid quantum properties.

We explore the influence of geometry in the critical behavior of sparse long-range spin models. We examine a model with interactions that can be continuously tuned to induce distinct changes in the metric, topology, and dimensionality of the coupling graph. This underlying geometry acts as the driver of criticality, with structural changes in the graph coinciding with and dictating the phase boundaries. We further discuss how this framework connects naturally to realizations in tweezer arrays with Rydberg excitations. In certain cases, the effective geometry can be incorporated in the layout of atoms in tweezers to realize phase transitions that preserve universal features, simplifying their implementation in near-term experiments.

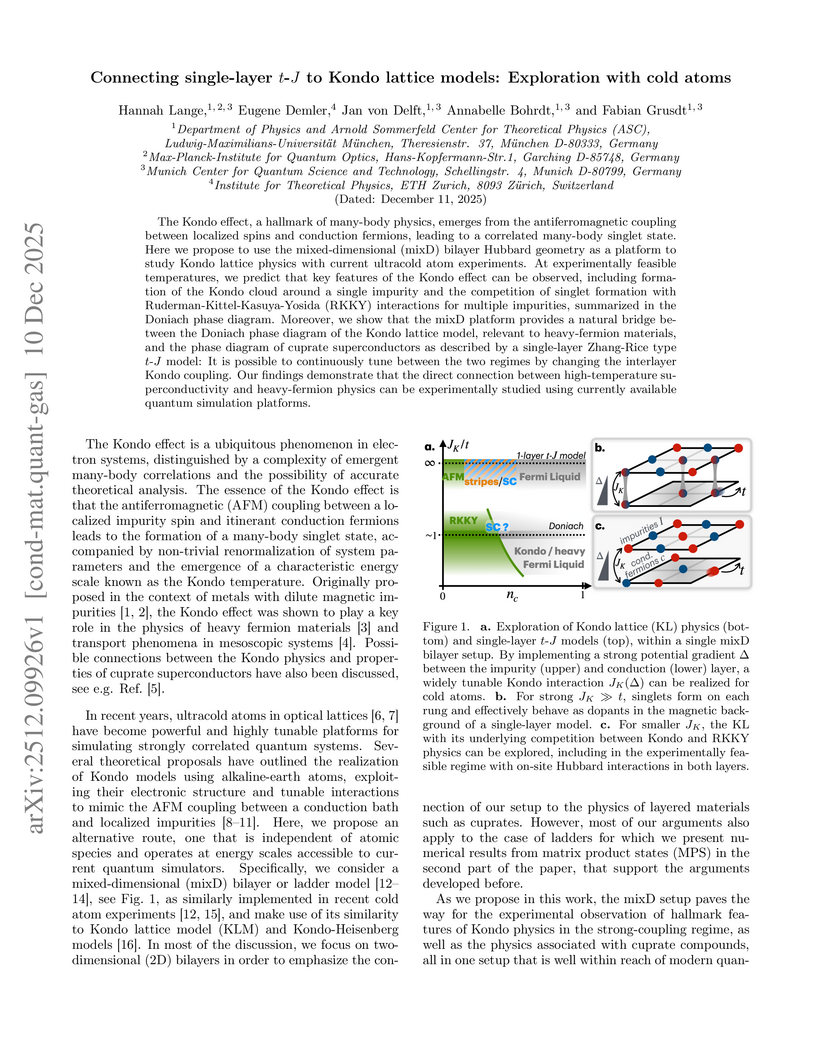
The Kondo effect, a hallmark of many-body physics, emerges from the antiferromagnetic coupling between localized spins and conduction fermions, leading to a correlated many-body singlet state. Here we propose to use the mixed-dimensional (mixD) bilayer Hubbard geometry as a platform to study Kondo lattice physics with current ultracold atom experiments. At experimentally feasible temperatures, we predict that key features of the Kondo effect can be observed, including formation of the Kondo cloud around a single impurity and the competition of singlet formation with Ruderman-Kittel-Kasuya-Yosida (RKKY) interactions for multiple impurities, summarized in the Doniach phase diagram. Moreover, we show that the mixD platform provides a natural bridge between the Doniach phase diagram of the Kondo lattice model, relevant to heavy-fermion materials, and the phase diagram of cuprate superconductors as described by a single-layer Zhang-Rice type $t$-$J$ model: It is possible to continuously tune between the two regimes by changing the interlayer Kondo coupling. Our findings demonstrate that the direct connection between high-temperature superconductivity and heavy-fermion physics can be experimentally studied using currently available quantum simulation platforms.

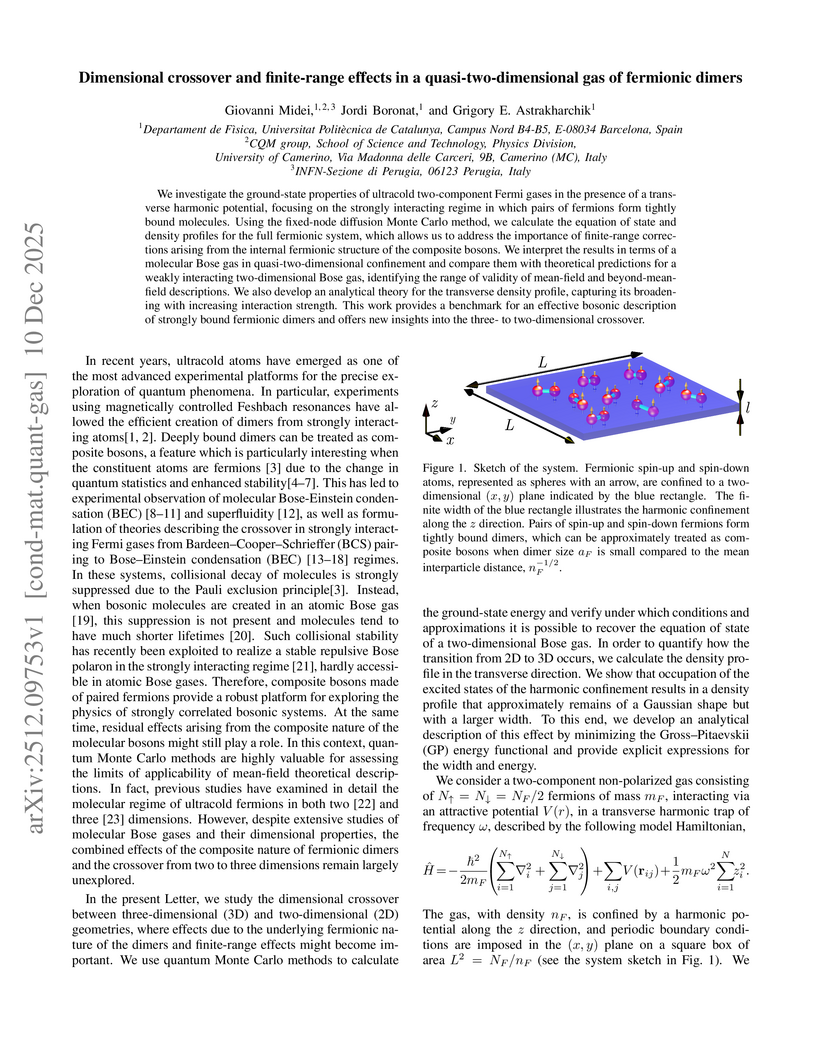
We investigate the ground-state properties of ultracold two-component Fermi gases in the presence of a transverse harmonic potential, focusing on the strongly interacting regime in which pairs of fermions form tightly bound molecules. Using the fixed-node diffusion Monte Carlo method, we calculate the equation of state and density profiles for the full fermionic system, which allows us to address the importance of finite-range corrections arising from the internal fermionic structure of the composite bosons. We interpret the results in terms of a molecular Bose gas in quasi-two-dimensional confinement and compare them with theoretical predictions for a weakly interacting two-dimensional Bose gas, identifying the range of validity of mean-field and beyond-mean-field descriptions. We also develop an analytical theory for the transverse density profile, capturing its broadening with increasing interaction strength. This work provides a benchmark for an effective bosonic description of strongly bound fermionic dimers and offers new insights into the three- to two-dimensional crossover.

Ultracold multicomponent fermions (atoms/molecules) loaded in optical lattices provide an ideal platform for simulating SU($N$) Hubbard models that host unconventional many-body quantum states beyond SU(2). A prime example is the attractive three-color Hubbard model, in which trion states emerge at strong coupling. Nevertheless, much of its trion ordering on two-dimensional lattices remains uncertain. Here, we employ the determinant quantum Monte Carlo (DQMC) method to simulate the attractive three-color Hubbard model on a $\pi$-flux square lattice at half filling. We show that color-dependent attractive interaction can induce coexisting charge density wave (CDW) and Néel ordered states in the three-color $\pi$-flux Hubbard model. In particular, enhanced charge fluctuations (cf. honeycomb lattice) cause much stronger Néel ordering on the $\pi$-flux square lattice. The coexisting charge and Néel orders survive up to a melting temperature, at which they vanish simultaneously. The Ginzburg-Landau (GL) analysis on the coexistence of CDW and Néel orders demonstrates how color-dependent Hubbard interactions stabilize coexisting orders from the perspective of GL free energy principle.

We report on an imaging scheme for quantum gases that enables simultaneous detection of two spin states with single-atom resolution. It utilizes the polarization of the emitted photons during fluorescence by choosing appropriate internal states of lithium-6 atoms in a magnetic field. This scheme can readily be implemented to obtain in-situ spin correlations in a wide variety of experimental settings.

A superfluid flows without friction below a critical velocity, exhibiting zero drag force on impurities. Above this threshold, superfluidity breaks down, and the internal energy is redistributed into incoherent excitations such as vortices. We demonstrate that a finite-mass, mobile impurity immersed in a flowing two-dimensional paraxial superfluid of light can \textit{swim} against the superfluid current when this critical velocity is exceeded. This self-propulsion is achieved by the periodic emission of quantized vortex-antivortex pairs downstream, which impart an upstream recoil momentum that results in a net propulsive force. Analogous to biological systems that minimize effort by exploiting wake turbulence, the impurity harnesses this vortex backreaction as a passive mechanism of locomotion. Reducing the impurity dynamics to the motion of its center of mass and using a point-vortex model, we quantitatively describe how this mechanism depends on the impurity geometry and the surrounding flow velocity. Our findings establish a fundamental link between internal-energy dissipation in quantum fluids and concepts of self-propulsion in active-matter systems, and opens new possibilities for exploiting vortices for controlled quantum transport at the microscale.

Recent studies of delocalization-localization transitions in disordered quantum chains have highlighted the role of rare, chain-breaking events that favor localization, in particular for high-energy eigenstates related to many-body localization. In this context, we revisit the random-field XXZ spin-1/2 chain at zero temperature with ferromagnetic interactions, equivalent to interacting fermions or hard-core bosons in a random potential with attractive interactions. We argue that localization in this model can be characterized by chain-breaking events, which are probed by the extreme values of simple local observables, such as the on-site density or the local magnetization, that are readily accessible in both experiments and numerical simulations. Adopting a bosonic language, we study the disorder-induced Berezinskii-Kosterlitz-Thouless (BKT) quantum phase transition from superfluid (SF) to Bose glass (BG), and focus on the strong disorder regime where localization is driven by weak links. Based on high-precision density matrix renormalization group simulations, we numerically show that extreme local densities accurately capture the BKT transition, even for relatively short chains ranging from a few dozen to a hundred sites. We also discuss the SF-BG transition in the weak disorder regime, where finite-size effects pose greater challenges. Overall, our work seeks to establish a solid foundation for using extreme statistics of local observables, such as density, to probe delocalization-localization transitions in disordered quantum chains, both in the ground state and at high energy.

We investigate thermalization and time-dependent Bose-Einstein condensate formation in ultracold Dy-164 using a nonlinear boson diffusion equation. As compared to alkali atoms such as K-39 or Rb-87, the strong magnetic dipole interaction modifies the scattering-length dependence of the transport coefficients that govern thermalization and condensate formation. A prediction for the time-dependent condensate fraction in Dy-164 is made.

Cavity quantum electrodynamics with atomic ensembles is typically associated with collective spin phenomena, such as superradiance and spin squeezing, in which the atoms evolve collectively as a macroscopic spin ($S\sim N/2$) on the Bloch sphere. Surprisingly, we show that the tendency toward a collective spin description need not imply collective spin phenomena; rather, it can be exploited to generate new forms of strongly correlated quantum matter. The key idea is to use uniform cavity-mediated interactions to energetically project the system into the total-spin singlet sector ($S=0$) - a highly entangled subspace where the physics is governed entirely by cavity fluctuations. Focusing on Rydberg atom arrays coupled to a single-mode cavity, we show that global cavity fluctuations can effectively squeeze classical antiferromagnets into quantum spin liquids, characterized by non-local entanglement, fractionalized excitations, and emergent gauge fields. This work suggests that cavity QED can be a surprising resource for inducing strongly correlated phenomena, which could be explored in the new generation of hybrid tweezer-cavity platforms.

The Sachdev-Ye-Kitaev (SYK) model has attracted widespread attention due to its relevance to diverse areas of physics, such as high temperature superconductivity, black holes, and quantum chaos. The model is, however, extremely challenging to realize experimentally. In this work, we show how a particular form of Floquet engineering, termed ``kinetic driving'', effectively eliminates single-particle processes and creates quasi-random all-to-all interactions when applied to models of Hubbard type. For the specific case of the Bose-Hubbard model, we explicitly verify that the driven system indeed reproduces SYK physics by direct comparison of the spectral form factor and out-of-time ordered correlation functions (OTOCs). Our findings indicate that a cold-atom realization of kinetic driving -- achieved through modulation of hopping amplitudes in an optical lattice -- offers a practical and accurate platform for quantum simulation of the SYK model.

We study the ferromagnetic instability in an SU($N$) Fermi-Hubbard model on the hypercubic lattice. Combining dynamical mean-field theory with continuous-time quantum Monte Carlo simulations, we find that, in the strong-coupling regime at low temperatures, ferromagnetically ordered (FM) states develop away from the commensurate fillings. In the particle-doped SU($3$) system near one-third filling, the FM state is accompanied by a spontaneous flavor-selective Mott state, where two of the three flavors are Mott insulating while the remaining flavor is metallic. Since particles in the metallic flavor can almost freely move on the lattice without correlation effects, the ordered state is stabilized by the kinetic-energy gain of the doped particles. This is similar to the generalized Nagaoka ferromagnetism discussed in the one-hole-doped system at one-third filling. In the SU($4$) case, we find that six distinct types of FM states appear as the particle density varies. The results uncover the nature of the FM state in the SU($N$) Fermi-Hubbard systems and highlight the rich magnetic behavior enabled by enlarged internal symmetries.

We propose a microscopic, weak-coupling mechanism by which generic Chern bands relax toward ideal bands. We consider coupling interacting electrons to a Caldeira-Leggett like Ohmic bosonic bath. Using the Born-Markov approximation, Slater determinant states of a Chern band under Hartree-Fock approximation evolve toward Slater determinant states corresponding to an ideal Chern band. We validate our proposal by performing numerical simulation of a massive Dirac model, showing that the Berry curvature and quantum metric indeed co-evolve to saturate the trace condition. Our proposal provides a concrete dissipative route to realize ideal Chern bands, a fundamental building block for the stabilization of fractional Chern insulators.

Symmetry breaking underlies diverse phenomena from phase transitions in condensed matter to fundamental interactions in gauge theories. Despite many proposed indicators, a general quantification of symmetry breaking that is faithful, computable, and valid in the thermodynamic limit has remained elusive. Here, within quantum resource theory, we propose the quantum Fisher information (QFI) as such a measure. We demonstrate its utility by computing QFI for paradigmatic models: in the BCS superconductor, the QFI counts the number of Cooper pairs; in the transverse-field XY spin chains, it captures topological phase transition that has no local order parameter; and in quantum quench dynamics, it allows us to exactly derive the microscopic origin and conditions of the quantum Mpemba effect in terms of excitation propagation, including in the thermodynamic limit--beyond the reach of previous analyses. Our results show that the QFI, which is a complete resource monotone in the resource theory of asymmetry that plays the role of entanglement entropy in entanglement theory, faithfully captures symmetry breaking in condensed-matter systems. These results highlight the QFI as a universal and physically meaningful diagnostic of symmetry breaking in both equilibrium and non-equilibrium quantum many-body systems.