We demonstrate a significant speedup of variational quantum algorithms that use discrete variable boson sampling when the parametrised phase shifters are constrained to have two distinct eigenvalues. This results in a cost landscape with less local minima and barren plateaus regardless of the problem, ansatz or circuit layout. This works without reliance on any classical pre-processing and allows for the fast gradient-free Rotosolve algorithm to be used. We propose three ways to achieve this by using either non-linear optics, measurement-induced non-linearities, or entangled resource states simulating fermionic statistics. The latter two require linear optics only, allowing for implementation with widely-available technology today. We show this outperforms the best-known boson sampling variational algorithm for all tests we conducted.

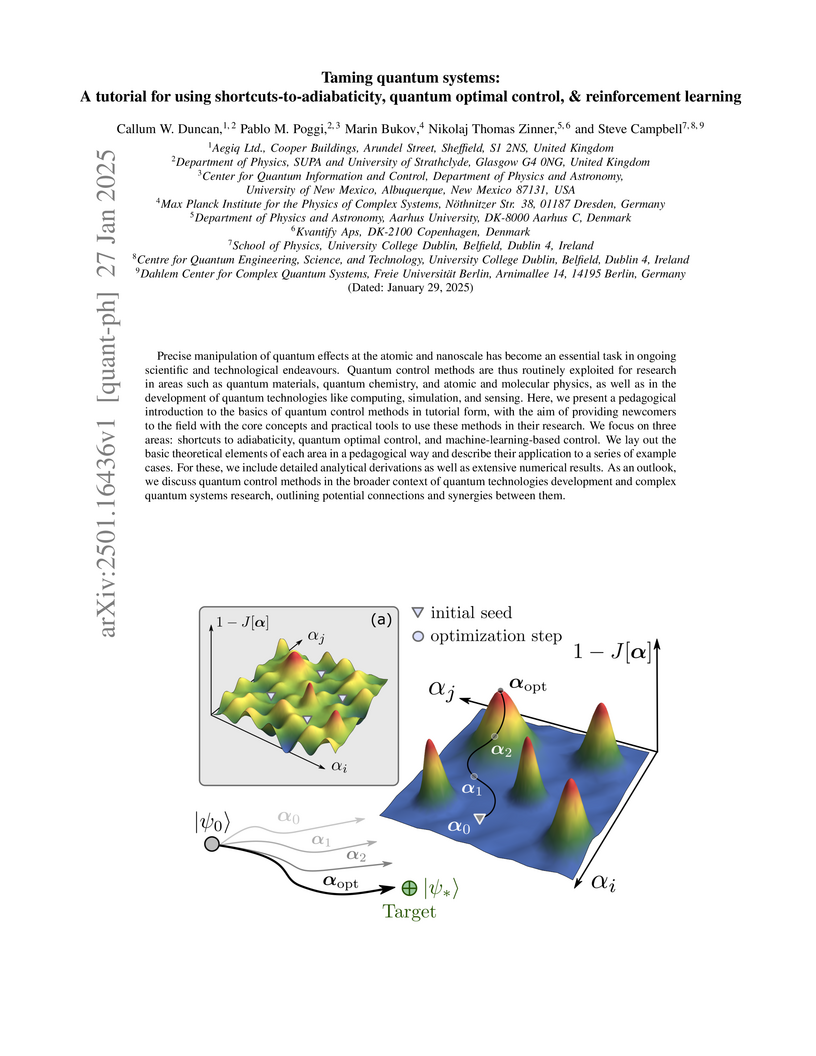
Precise manipulation of quantum effects at the atomic and nanoscale has become an essential task in ongoing scientific and technological endeavours. Quantum control methods are thus routinely exploited for research in areas such as quantum materials, quantum chemistry, and atomic and molecular physics, as well as in the development of quantum technologies like computing, simulation, and sensing. Here, we present a pedagogical introduction to the basics of quantum control methods in tutorial form, with the aim of providing newcomers to the field with the core concepts and practical tools to use these methods in their research. We focus on three areas: shortcuts to adiabaticity, quantum optimal control, and machine-learning-based control. We lay out the basic theoretical elements of each area in a pedagogical way and describe their application to a series of example cases. For these, we include detailed analytical derivations as well as extensive numerical results. As an outlook, we discuss quantum control methods in the broader context of quantum technologies development and complex quantum systems research, outlining potential connections and synergies between them.

Measurement-based quantum computing relies on the generation of large entangled cluster states that act as a universal resource on which logical circuits can be imprinted and executed through local measurements. A number of strategies for constructing sufficiently large photonic cluster states propose fusing many smaller resource states generated by a series of quantum emitters. However, the fusion process is inherently probabilistic with a 50% success probability in standard guise. A recent proposal has shown that, in the limit of low loss, the probability of achieving successful fusion may be boosted to near unity by redundantly encoding the vertices of linear graph states using Greenberger-Horne-Zeilinger states [Quantum 7, 992 (2023)]. Here we present a protocol for deterministically generating redundantly encoded photonic resource states using single quantum emitters, and study the impact of protocol errors and photonic losses on the generated resource states and type-II photonic fusion. Our work provides a route for efficiently constructing complex entangled photonic qubit states for photonic quantum computing and quantum repeaters.

We present a universal quantum computing architecture which combines the measurement-driven aspect of MBQC with the circuit model's algorithm dependent generation of qubit entanglement. Our architecture, which we call QGATE, is tailored for discrete-variable photonic quantum computers with deterministic photon sources capable of generating 1D entangled photonic states. QGATE achieves universal quantum computing on a logical data qubit register via the implementation of Clifford operations, QGATE ancilla, and arbitrary angle single-qubit measurements. We realise unitary evolutions defined by multi-qubit Pauli strings via the generation of entanglement between a sub-set of logical qubits and a mutual QGATE ancilla qubit. Measurement of the QGATE ancilla in the appropriate basis then implements a given term of the desired unitary operation. This enables QGATE to both directly perform Hamiltonian evolutions in terms of a series of multi-qubit Pauli operators, in terms of projectors for an arbitrary sparse Hamiltonian, or realise multi-controlled gates enabling direct translation of circuit models to QGATE. We consider examples inspired by quantum chemistry and computational fluid dynamics. We propose an example photonic implementation of QGATE and calculate thresholds of $10.36\pm0.02\%$ or $25.98\pm0.28\%$ on the photonic loss for logical qubits constructed from foliated rotated surface codes, dependent on the deployment of intra-layer or inter-layer fusion respectively.

Disordered potentials fundamentally alter the transport properties and coherence of quantum systems. They give rise to phenomena such as Anderson localization in non-interacting systems, inhibiting transport. When interactions are introduced, the interplay with disorder becomes significantly more complex, and the conditions under which localization can be observed remain an open question. In interacting bosonic systems, a Bose glass is expected to emerge at low energies as an insulating yet compressible state without long-range phase coherence. While originally predicted to occur as a ground-state phase, more recent studies indicate that it exists at finite temperature. A key open challenge has been the direct observation of reduced phase coherence in the Bose-glass regime. In this study, we utilize ultracold bosonic atoms in a quantum-gas microscope to probe the emergence of the Bose-glass phase in a two-dimensional square lattice with a site-resolved, reproducible disordered potential. We identify the phase through in-situ distribution and particle fluctuations, via a local measurement of the Edwards-Anderson parameter. To measure the short-range phase coherence in the Bose glass, we employ Talbot interferometry in combination with single-atom-resolved detection. Finally, by driving the system in and out of the Bose-glass phase, we observe signatures for non-ergodic behavior.

The Gross-Pitaevskii equation and its generalisations to dissipative and dipolar gases have been very useful in describing dynamics of cold atomic gases, as well as polaritons and other nonlinear systems. For some of these applications the numerically accessible grid spacing can become a limiting factor, especially in describing turbulent dynamics and short-range effects of dipole-dipole interactions. We explore the application of tensor networks to these systems, where (in analogy to related work in fluid and plasma dynamics), they allow for physically motivated data compression that makes simulations possible on large spatial grids which would be unfeasible with direct numerical simulations. Analysing different non-equilibrium cases involving vortex formation, we find that these methods are particularly efficient, especially in combination with a matrix product operator representation of the quantum Fourier transform, which enables a spectral approach to calculation of both equilibrium states and time-dependent dynamics. The efficiency of these methods has interesting physical implications for the structure in the states that are generated by these dynamics, and provides a path to describe cold gas experiments that are challenging for existing methods.

Counterdiabatic driving, which enforces adiabatic evolution in arbitrary timescales, can be realised by engineering a Floquet Hamiltonian which oscillates between the Hamiltonian and its derivative requiring no additional control terms. However, the coefficients of the Floquet Hamiltoinan require knowledge of the counterdiabatic terms, which can be difficult to derive outside of a limited set of examples. We introduce a new hybrid technique for the control of quantum systems, Counterdiabatic-influenced Floquet-engineering or CAFFEINE for short. CAFFEINE parameterises the Floquet Hamiltonian for counterdiabatic driving and utilises numerical quantum optimal control in order to obtain the desired target state. This removes the need to both obtain and implement counterdiabatic terms, however, it does require the ability to quickly oscillate each term in the Hamiltonian. If this oscillation is possible, then CAFFEINE provides a framework to implement quantum annealing protocols and general quantum state preparation. We illustrate this through optimisation of two numerical examples of preparing a Bell state with two qubits and performing annealing protocols for the one-dimensional Ising model. Beyond this, we also illustrate CAFFEINE's capabilities to learn the counterdiabatic terms, which can potentially be used as a probe of quantum chaos and the geometry of quantum dynamics.

There is currently significant interest in emulating the essential characteristics of black holes, such as their Hawking radiation or their optimal scrambling behavior, using condensed matter models. In this article, we investigate a chiral spin-chain, whose mean field theory effectively captures the behavior of Dirac fermions in the curved spacetime geometry of a black hole. We find that within the region of the chain that describe the interior of the black hole, strong correlations prevail giving rise to many-body chaotic dynamics. Employing out-of-time-order correlations as a diagnostic tool, we numerically compute the associated Lyapunov exponent. Intriguingly, we observe a linear increase in the Lyapunov exponent with temperature within the black hole's interior at low temperatures, indicative of optimal scrambling behavior. This contrasts with the quadratic temperature dependence exhibited by the spin-chain on the region outside the black hole. Our findings contribute to a deeper understanding of the interplay between black hole geometry and quantum chaos, offering insights into fundamental aspects of quantum gravity.

In this paper we explore the properties of a 1-dimensional spin chain in the presence of chiral interactions, focusing on the system's transition to distinct chiral phases for various values of the chiral coupling. By employing the mean field theory approximation we establish a connection between this chiral system and a Dirac particle in the curved spacetime of a black hole. Surprisingly, the black hole horizon coincides with the interface between distinct chiral phases. We examine the chiral properties of the system for homogeneous couplings and in scenarios involving position dependent couplings that correspond to black hole geometries. To determine the significance of interactions in the chiral chain we employ bosonization techniques and derive the corresponding Luttinger liquid model. Furthermore, we investigate the classical version of the model to understand the impact of the chiral operator on the spins and gain insight into the observed chirality. Our findings shed light on the behavior of the spin chain under the influence of the chiral operator, elucidating the implications of chirality in various contexts, including black hole physics.