It is commonly recognized that the primordial scalar spectral index $n_s$ is approximately $0.96-0.975$, depending on the dataset. However, this view is being completely altered by the early dark energy (EDE) resolutions of the Hubble tension, known as the most prominent tension the standard $\Lambda$CDM model is suffering from. In corresponding models with pre-recombination EDE, resolving the Hubble tension (i.e., achieving $H_0\sim 73$km/s/Mpc) must be accompanied by a shift of $n_s$ towards unity to maintain consistency with the cosmological data, which thus implies a scale invariant Harrison-Zel'dovich spectrum with $n_s=1$ $(|n_s-1|\simeq {\cal O}(0.001))$. In this work, we strengthen and reconfirm this result with the latest ground-based CMB data from ACT DR6 and SPT-3G D1, the precise measurements at high multipoles beyond the Planck angular resolution and sensitivity. Our work again highlights the importance of re-examining our understanding on the very early Universe within the broader context of cosmological tensions.

With the help of a given distance matrix of size $n$, we construct an infinite family of distances $d_p$ (where $p \geq 2$) on the the complex projective space $\mathbb{P}(\mathbb{C}^n)$, modelling the space of pure states of an $n$-dimensional quantum system. The construction can be seen as providing a natural way to isometrically embed any given finite metric space into the space of pure quantum states 'spanned' upon it. In order to show that the maps $d_p$ are indeed distance functions -- in particular, that they satisfy the triangle inequality -- we employ methods of analysis, multilinear algebra and convex geometry, obtaining a non-trivial convexity result in the process. The paper significantly extends earlier work, resolving an important question about the geometry of quantum state space imposed by the quantum Wasserstein distances and solidifying the foundation for applications of distances $d_p$ in quantum information science.

We present constraints on cosmological parameters using maps from the last Planck data release (PR4). In particular, we detail an upgraded version of the cosmic microwave background likelihood, HiLLiPoP, based on angular power spectra and relying on a physical modelling of the foreground residuals in the spectral domain. This new version of the likelihood retains a larger sky fraction (up to 75%) and uses an extended multipole range. Using this likelihood, along with low-l measurements from LoLLiPoP, we derive constraints on $\Lambda$CDM parameters that are in good agreement with previous Planck 2018 results, but with 10% to 20% smaller uncertainties. We demonstrate that the foregrounds can be accurately described in spectra domain with only negligible impact on $\Lambda$CDM parameters. We also derive constraints on single-parameter extensions to $\Lambda$CDM including $A_L$, $\Omega_K$, $N_{eff}$, and $\sum m_{\nu}$. Noteworthy results from this updated analysis include a lensing amplitude value of $A_L = 1.039 \pm 0.052$, which aligns more closely with theoretical expectations within the $\Lambda$CDM framework. Additionally, our curvature measurement, $\Omega_K = -0.012 \pm 0.010$, now demonstrates complete consistency with a flat universe, and our measurement of $S_8$ is closer to the measurements derived from large-scale structure surveys (at the 1.6$\sigma$ level). We also add constraints from PR4 lensing, making the combination the most constraining data set that is currently available from Planck. Additionally we explore adding baryon acoustic oscillation data, which tightens limits on some particular extensions to the standard cosmology.

We investigate black hole superradiance evolution of the interacting multiple fields. We consider a model of two scalar fields interacting with a cubic coupling, and study the superradiant evolution of the cloud. We demonstrate that superradiance is typically suppressed when the superradiant field couples to another field, even with a very weak coupling strength. This implies that the constraints on dark particles derived from single-field analyses can be revised in the presence of interactions. Moreover, we find that the multi-field superradiant evolution and its corresponding observational signatures can be different across parameter spaces, which makes black hole superradiance an even more powerful probe of the dark sector in particle physics.

It has been noted that with the pre-recombination early dark energy (EDE) resolution of Hubble tension, the preference of recent datasets for the evolving dark energy (DE) can be suppressed significantly. In this work, we clarify and reconfirm this result with DESI DR2 and the latest ACT DR6 and SPT-3G D1, the tightest small-scale CMB constraints up to date. In the $w_0w_a$CDM model with EDE, a quintessence-like component ($w_0+w_a\geq-1$) can be 1$\sigma$ consistent with Planck+ACT+SPT+DESI+Pantheon+SH0ES datasets, and $\Delta\chi^2\lesssim -14$ compared with $w_0w_a$CDM model without EDE. This reveals the possibility that when the potential resolutions of Hubble tension are considered, current accelerated expansion can attribute to a canonical evolving scalar field or cosmological constant, and again highlights the importance of re-examining the nature of DE within the broader context of cosmological tensions.

We study the dual CFT description of the $d+1$-dimensional Reissner-Nordström-Anti de Sitter (RN-AdS$_{d+1}$) black hole in the large dimension (large $d$) limit, both for the extremal and nonextremal cases. The central charge of the dual CFT$_2$ (or chiral CFT$_1$) is calculated for the near horizon near extremal geometry which possess an AdS$_2$ structure. Besides, the $Q$-picture hidden conformal symmetry in the nonextremal background can be naturally obtained by a probe charged scalar field in the large $d$ limit, without the need to input the usual limits to probe the hidden conformal symmetry. Furthermore, an new dual CFT description of the nonextremal RN-AdS$_{d+1}$ black hole is found in the large $d$ limit and the duality is analyzed by comparing the entropies, the absorption cross sections and the retarded Green's functions obtained both from the gravity and the dual CFT sides.

Quantum field theory (QFT) for interacting many-electron systems is fundamental to condensed matter physics, yet achieving accurate solutions confronts computational challenges in managing the combinatorial complexity of Feynman diagrams, implementing systematic renormalization, and evaluating high-dimensional integrals. We present a unifying framework that integrates QFT computational workflows with an AI-powered technology stack. A cornerstone of this framework is representing Feynman diagrams as computational graphs, which structures the inherent mathematical complexity and facilitates the application of optimized algorithms developed for machine learning and high-performance computing. Consequently, automatic differentiation, native to these graph representations, delivers efficient, fully automated, high-order field-theoretic renormalization procedures. This graph-centric approach also enables sophisticated numerical integration; our neural-network-enhanced Monte Carlo method, accelerated via massively parallel GPU implementation, efficiently evaluates challenging high-dimensional diagrammatic integrals. Applying this framework to the uniform electron gas, we determine the quasiparticle effective mass to a precision significantly surpassing current state-of-the-art simulations. Our work demonstrates the transformative potential of integrating AI-driven computational advances with QFT, opening systematic pathways for solving complex quantum many-body problems across disciplines.

The holographic entanglement entropy of an infinite strip subsystem on the asymptotic AdS boundary is used as a probe to study the thermodynamic instabilities of planar R-charged black holes (or their dual field theories). We focus on the single-charge AdS black holes in $D=5$, which correspond to spinning D3-branes with one non-vanishing angular momentum. Our results show that the holographic entanglement entropy indeed exhibits the thermodynamic instability associated with the divergence of the specific heat. When the width of the strip is large enough, the finite part of the holographic entanglement entropy as a function of the temperature resembles the thermal entropy, as is expected. As the width becomes smaller, however, the two entropies behave differently. In particular, there exists a critical value for the width of the strip, below which the finite part of the holographic entanglement entropy as a function of the temperature develops a self-intersection. We also find similar behavior in the single-charge black holes in $D=4$ and $7$.

The mass transfer process is prevalent during the inspiral phase of compact binary systems. Detection of gravitational waves from the inspiral phase of binaries with white dwarfs will allow us to measure the mass transfer rate. Mass transfer effects provide additional contributions to the phase of gravitational waves, which can break the degeneracy between binary masses and redshift. Based on the analytic mass transfer rate to the first order post-Newtonian evolution of orbital angular frequency, we use the Fisher matrix to forecast the ability of DECIGO to measure the redshift of compact binaries with mass transfer. We conclude that for compact binary systems containing white dwarfs, the redshift can be determined to an accuracy of $10\%$ for $z=0.01$ with a $SNR\thicksim 30$.

We present an experimental demonstration of heralded single photons prepared in pure quantum states from a parametric downconversion source. It is shown that, through controlling the modal structure of the photon pair emission, one can generate pairs in factorable states and thence eliminate the need for spectral filters in multiple-source interference schemes. Indistinguishable heralded photons were generated in two independent spectrally engineered sources, and, by performing a Hong-Ou-Mandel interference between them without spectral filters at a raw visibility of 94.4%, their purity was measured to be over 95%.

This thesis contains of two parts: The first part is a pedagogical introduction into the field of bosonic SFT. After discussing some general properties we expect, Witten's open SFT and Zwiebach's closed SFT are presented in detail. This means we set up the action, explain the algebraical and geometrical structure and mention physical applications. In the open case we review the most important analytic solutions including the necessary operator technology whileas in the closed case we focus on quantization and the more elaborate construction of the vertices. The second part contains of reprints of papers completed within the PhD: 2301.13182, 2402.00308, 2410.16228 and 2411.15123.

We perform a search for light sterile neutrinos using the data from the T2K far detector at a baseline of 295 km, with an exposure of 14.7 (7.6)$\times 10^{20}$ protons on target in neutrino (antineutrino) mode. A selection of neutral current interaction samples are also used to enhance the sensitivity to sterile mixing. No evidence of sterile neutrino mixing in the 3+1 model was found from a simultaneous fit to the charged-current muon, electron and neutral current neutrino samples. We set the most stringent limit on the sterile oscillation amplitude $\sin^2\theta_{24}$ for the sterile neutrino mass splitting \Delta m^2_{41}<3\times 10^{-3} eV$^2/c^4$.

Gravitational waves undergo redshift as they propagate through the expanding universe, and the redshift may exhibit time-dependent drift. Consequently, for any isolated gravitational wave sources, the mass parameter $\mathcal{M}$ and the redshift $z$ exhibit an observational degeneracy, typically manifesting in the waveform as the redshifted mass $\mathcal{M}(1+z)$. Matching together the wave propagation and the wave generation solutions, we show that dimensionless source parameters depending on mass $\mathcal{M}$ can break this degeneracy. Notably, the postmerger signal from binary neutron stars contains several dimensionless parameters that satisfy this condition, including the quality factors of different frequency components and their frequency ratios. Considering the observations of solely the postmerger signal by the Neutron star Extreme Matter Observatory or the Einstein Telescope, based on the Fisher analysis, we find that the redshift can be measured with fractional uncertainties of $\sim30\%$ for sources at $0.01

It was found by Hung, Myers and Smolkin that there is entropy discrepancy for the CFTs in 6-dimensional space-time, between the field theoretical and the holographic analysis. Recently, two different resolutions to this puzzle have been proposed. One of them suggests to utilize the anomaly-like entropy and the generalized Wald entropy to resolve the HMS puzzle, while the other one initiates to use the entanglement entropy which arises from total derivative terms in the Weyl anomaly to explain the HMS mismatch. We investigate these two proposals carefully in this note. By studying the CFTs dual to Einstein gravity, we find that the second proposal can not solve the HMS puzzle. Moreover, the Wald entropy formula is not well-defined on horizon with extrinsic curvatures, in the sense that, in general, it gives different results for equivalent actions.

The quasinormal modes (QNMs) of a rotating quantum corrected black hole (RQCBH) are studied by employing the hyperboloidal framework for the scalar perturbation. This framework is used to cast the QNMs spectra problem into the two-dimensional eigenvalues problem, then the spectra are calculated by imposing two-dimensional pseudo-spectral method. Based on the resulting spectra, a parameter estimation pipeline for this RQCBH model with gravitational wave data is constructed by using \texttt{pyRing} in the ringdown phase. We find that, even when the RQCBH spectra exhibits a small deviation from the Kerr spectra, the strong correlation between the extra parameter coming from the quantum gravity theory and the intrinsic parameter of black hole may significantly affect the posterior distributions of the mass $M$ and the dimensionless spin $\bar{a}$.

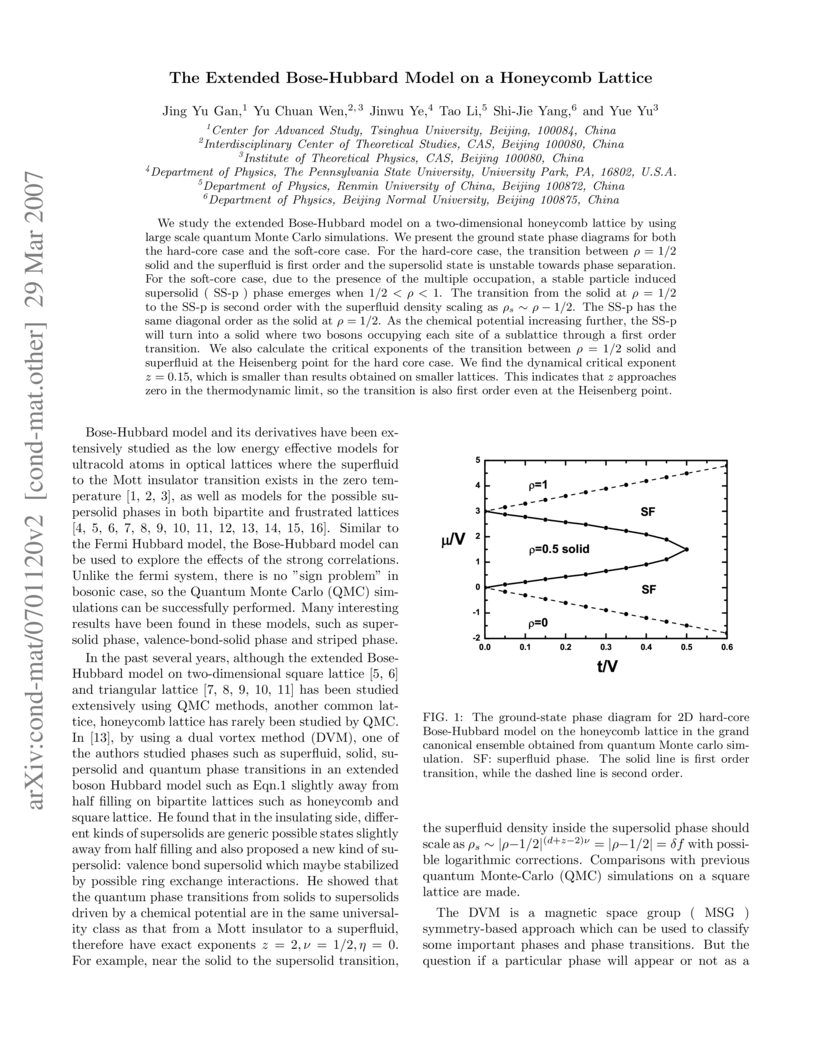
We study the extended Bose-Hubbard model on a two-dimensional honeycomb lattice by using large scale quantum Monte Carlo simulations. We present the ground state phase diagrams for both the hard-core case and the soft-core case. For the hard-core case, the transition between $\rho=1/2$ solid and the superfluid is first order and the supersolid state is unstable towards phase separation. For the soft-core case, due to the presence of the multiple occupation, a stable particle induced supersolid (SS-p) phase emerges when 1/2<\rho<1. The transition from the solid at $\rho=1/2$ to the SS-p is second order with the superfluid density scaling as $\rho_{s} \sim \rho-1/2$. The SS-p has the same diagonal order as the solid at $\rho=1/2$. As the chemical potential increasing further, the SS-p will turn into a solid where two bosons occupying each site of a sublattice through a first order transition. We also calculate the critical exponents of the transition between $\rho=1/2$ solid and superfluid at the Heisenberg point for the hard core case. We find the dynamical critical exponent $z=0.15$, which is smaller than results obtained on smaller lattices. This indicates that $z$ approaches zero in the thermodynamic limit, so the transition is also first order even at the Heisenberg point.

Geometrical structures intrinsic to non-expanding, weakly isolated and isolated horizons are analyzed and compared with structures which arise in other contexts within general relativity, e.g., at null infinity. In particular, we address in detail the issue of singling out the preferred normals to these horizons required in various applications. This work provides powerful tools to extract invariant, physical information from numerical simulations of the near horizon, strong field geometry. While it complements the previous analysis of laws governing the mechanics of weakly isolated horizons, prior knowledge of those results is not assumed.

In this work the determination of low-energy bound states in Quantum Chromodynamics is recast so that it is linked to a weak-coupling problem. This allows one to approach the solution with the same techniques which solve Quantum Electrodynamics: namely, a combination of weak-coupling diagrams and many-body quantum mechanics. The key to eliminating necessarily nonperturbative effects is the use of a bare Hamiltonian in which quarks and gluons have nonzero constituent masses rather than the zero masses of the current picture. The use of constituent masses cuts off the growth of the running coupling constant and makes it possible that the running coupling never leaves the perturbative domain. For stabilization purposes an artificial potential is added to the Hamiltonian, but with a coefficient that vanishes at the physical value of the coupling constant. The weak-coupling approach potentially reconciles the simplicity of the Constituent Quark Model with the complexities of Quantum Chromodynamics. The penalty for achieving this perturbative picture is the necessity of formulating the dynamics of QCD in light-front coordinates and of dealing with the complexities of renormalization which such a formulation entails. We describe the renormalization process first using a qualitative phase space cell analysis, and we then set up a precise similarity renormalization scheme with cutoffs on constituent momenta and exhibit calculations to second order. We outline further computations that remain to be carried out. There is an initial nonperturbative but nonrelativistic calculation of the hadronic masses that determines the artificial potential, with binding energies required to be fourth order in the coupling as in QED. Next there is a calculation of the leading radiative corrections to these masses, which requires our renormalization program. Then the real struggle of finding the right extensions to perturbation theory to study the strong-coupling behavior of bound states can begin.

Solar neutrino measurements from 1258 days of data from the Super-Kamiokande detector are presented. The measurements are based on recoil electrons in the energy range 5.0-20.0MeV. The measured solar neutrino flux is 2.32 +- 0.03(stat.) +0.08-0.07(sys.)*10^6cm^{-2}s^{-1}, which is 45.1+-0.5(stat.)+1.6-1.4(sys.)% of that predicted by the BP2000 SSM. The day vs night flux asymmetry is 0.033+-0.022(stat.)+0.013-0.012(sys.). The recoil electron energy spectrum is consistent with no spectral distortion (\chi^2/d.o.f. = 19.0/18). The seasonal variation of the flux is consistent with that expected from the eccentricity of the Earth's orbit (\chi^2/d.o.f. = 3.7/7). For the hep neutrino flux, we set a 90% C.L. upper limit of 40 *10^3cm^{-2}s^{-1}, which is 4.3 times the BP2000 SSM prediction.

We study the thermoelectric transport under shear strain in two spatial dimensional quantum matter using the holographic duality. General analytic formulae for the DC thermoelectric conductivities subjected to finite shear strain are obtained in terms of the black hole horizon data. Off-diagonal terms in the conductivity matrix appear also at zero magnetic field, resembling an emergent electronic nematicity which cannot nevertheless be identified with the presence of an anomalous Hall effect. For an explicit model study, we numerically construct a family of strained black holes and obtain the corresponding nonlinear stress-strain curves. We then compute all electric, thermoelectric, and thermal conductivities and discuss the effects of strain. While the shear elastic deformation does not affect the temperature dependence of thermoelectric and thermal conductivities quantitatively, it can strongly change the behavior of the electric conductivity. For both shear hardening and softening cases, we find a clear metal-insulator transition driven by the shear deformation. Moreover, the violation of the previously conjectured thermal conductivity bound is observed for large shear deformation.