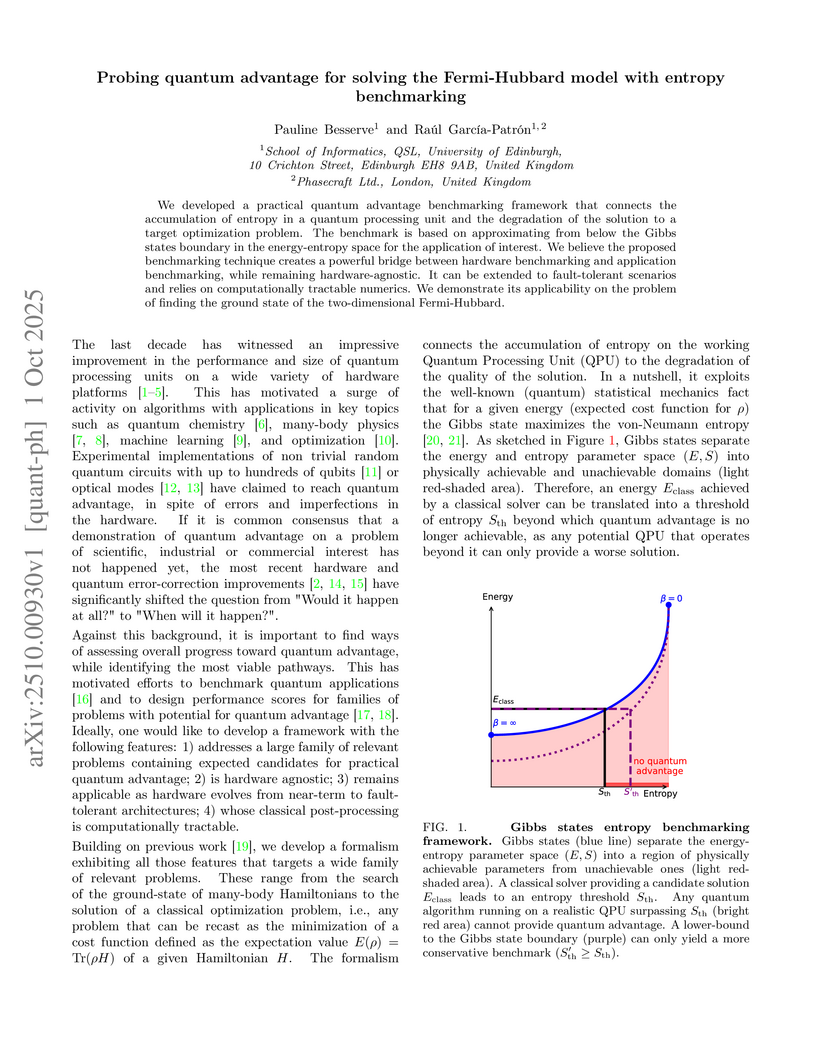
We developed a practical quantum advantage benchmarking framework that connects the accumulation of entropy in a quantum processing unit and the degradation of the solution to a target optimization problem. The benchmark is based on approximating from below the Gibbs states boundary in the energy-entropy space for the application of interest. We believe the proposed benchmarking technique creates a powerful bridge between hardware benchmarking and application benchmarking, while remaining hardware-agnostic. It can be extended to fault-tolerant scenarios and relies on computationally tractable numerics. We demonstrate its applicability on the problem of finding the ground state of the two-dimensional Fermi-Hubbard.

Decoding low-density parity-check codes is critical in many current technologies, such as fifth-generation (5G) wireless networks and satellite communications. The belief propagation algorithm allows for fast decoding due to the low density of these codes. However, there is scope for improvement to this algorithm both in terms of its computational cost when decoding large codes and its error-correcting abilities. Here, we introduce the quantum-enhanced belief propagation (QEBP) algorithm, in which the Quantum Approximate Optimization Algorithm (QAOA) acts as a pre-processing step to belief propagation. We perform exact simulations of syndrome decoding with QAOA, whose result guides the belief propagation algorithm, leading to faster convergence and a lower block error rate (BLER). In addition, through the repetition code, we study the possibility of having shared variational parameters between syndromes and, in this case, code lengths. We obtain a unique pair of variational parameters for level-1 QAOA by optimizing the probability of successful decoding through a transfer matrix method. Then, using these parameters, we compare the scaling of different QAOA post-processing techniques with code length.

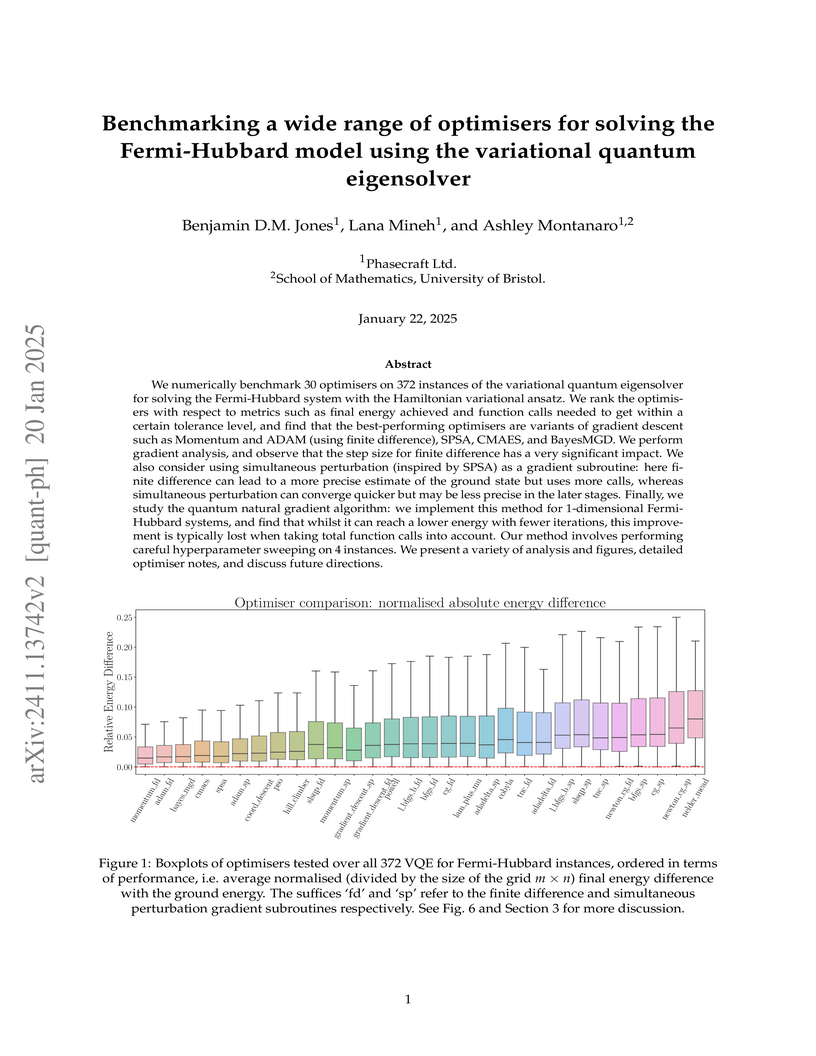
We numerically benchmark 30 optimisers on 372 instances of the variational quantum eigensolver for solving the Fermi-Hubbard system with the Hamiltonian variational ansatz. We rank the optimisers with respect to metrics such as final energy achieved and function calls needed to get within a certain tolerance level, and find that the best performing optimisers are variants of gradient descent such as Momentum and ADAM (using finite difference), SPSA, CMAES, and BayesMGD. We also perform gradient analysis and observe that the step size for finite difference has a very significant impact. We also consider using simultaneous perturbation (inspired by SPSA) as a gradient subroutine: here finite difference can lead to a more precise estimate of the ground state but uses more calls, whereas simultaneous perturbation can converge quicker but may be less precise in the later stages. Finally, we also study the quantum natural gradient algorithm: we implement this method for 1-dimensional Fermi-Hubbard systems, and find that whilst it can reach a lower energy with fewer iterations, this improvement is typically lost when taking total function calls into account. Our method involves performing careful hyperparameter sweeping on 4 instances. We present a variety of analysis and figures, detailed optimiser notes, and discuss future directions.

One of the most important quantities characterizing the microscopic properties of quantum systems are dynamical correlation functions. These correlations are obtained by time-evolving a perturbation of an eigenstate of the system, typically the ground state. In this work, we study approximations of these correlation functions that do not require time dynamics. We show that having access to a circuit that prepares an eigenstate of the Hamiltonian, it is possible to approximate the dynamical correlation functions up to exponential accuracy in the complex frequency domain $\omega=\Re(\omega)+i\Im(\omega)$, on a strip above the real line $\Im(\omega)=0$. We achieve this by exploiting the continued fraction representation of the dynamical correlation functions as functions of frequency $\omega$, where the level $k$ approximant can be obtained by measuring a weight $O(k)$ operator on the eigenstate of interest. In the complex $\omega$ plane, we show how this approach allows to determine approximations to correlation functions with accuracy that increases exponentially with $k$. We analyse two algorithms to generate the continuous fraction representation in scalar or matrix form, starting from either one or many initial operators. We prove that these algorithms generate an exponentially accurate approximation of the dynamical correlation functions on a region sufficiently far away from the real frequency axis. We present numerical evidence of these theoretical results through simulations of small lattice systems. We comment on the stability of these algorithms with respect to sampling noise in the context of quantum simulation using quantum computers.

The famous, yet unsolved, Fermi-Hubbard model for strongly-correlated electronic systems is a prominent target for quantum computers. However, accurately representing the Fermi-Hubbard ground state for large instances may be beyond the reach of near-term quantum hardware. Here we show experimentally that an efficient, low-depth variational quantum algorithm with few parameters can reproduce important qualitative features of medium-size instances of the Fermi-Hubbard model. We address 1x8 and 2x4 instances on 16 qubits on a superconducting quantum processor, substantially larger than previous work based on less scalable compression techniques, and going beyond the family of 1D Fermi-Hubbard instances, which are solvable classically. Consistent with predictions for the ground state, we observe the onset of the metal-insulator transition and Friedel oscillations in 1D, and antiferromagnetic order in both 1D and 2D. We use a variety of error-mitigation techniques, including symmetries of the Fermi-Hubbard model and a recently developed technique tailored to simulating fermionic systems. We also introduce a new variational optimisation algorithm based on iterative Bayesian updates of a local surrogate model. Our scalable approach is a first step to using near-term quantum computers to determine low-energy properties of strongly-correlated electronic systems that cannot be solved exactly by classical computers.

We present an approach, which we term quantum-enhanced optimization, to accelerate classical optimization algorithms by leveraging quantum sampling. Our method uses quantum-generated samples as warm starts to classical heuristics for solving challenging combinatorial problems like Max-Cut and Maximum Independent Set (MIS). To implement the method efficiently, we introduce novel parameter-setting strategies for the Quantum Approximate Optimization Algorithm (QAOA), qubit mapping and routing techniques to reduce gate counts, and error-mitigation techniques. Experimental results, including on quantum hardware, showcase runtime improvements compared with the original classical algorithms.

We construct a family of Hamiltonians whose phase diagram is guaranteed to have a single phase transition, yet the location of this phase transition is uncomputable. The Hamiltonians $H(\phi)$ describe qudits on a two-dimensional square lattice with translationally invariant, nearest-neighbour interactions tuned by a continuous parameter $\phi\in(0,1]$. For all $\phi\in(0,1]$, $H(\phi)$ is in one of two phases, one a gapless phase, the other a gapped phase. The phase transition occurs when $\phi$ equals the Chaitin's constant $\Omega$, a well-defined real number that encodes the Halting problem, and hence is uncomputable for Turing machines and undecidable for any consistent recursive axiomatization of mathematics. Our result implies that no general algorithm exists to determine the phase diagrams even under the promise that the phase diagram is exceedingly simple, and illustrates how uncomputable numbers may manifest in physical systems.

Simulation of materials is one of the most promising applications of quantum computers. On near-term hardware the crucial constraint on these simulations is circuit depth. Many quantum simulation algorithms rely on a layer of unitary evolutions generated by each term in a Hamiltonian. This appears in time-dynamics as a single Trotter step, and in variational quantum eigensolvers under the Hamiltonian variational ansatz as a single ansatz layer. We present a new quantum algorithm design for materials modelling where the depth of a layer is independent of the system size. This design takes advantage of the locality of materials in the Wannier basis and employs a tailored fermionic encoding that preserves locality. We analyse the circuit costs of this approach and present a compiler that transforms density functional theory data into quantum circuit instructions -- connecting the physics of the material to the simulation circuit. The compiler automatically optimises circuits at multiple levels, from the base gate level to optimisations derived from the physics of the specific target material. We present numerical results for materials spanning a wide structural and technological range. Our results demonstrate a reduction of many orders of magnitude in circuit depth over standard prior methods that do not consider the structure of the Hamiltonian. For example our results improve resource requirements for Strontium Vanadate (SrVO$_3$) from 864 to 180 qubits for a $3\times3\times3$ lattice, and the circuit depth of a single Trotter or variational layer from $7.5\times 10^8$ to depth $884$. Although this is still beyond current hardware, our results show that materials simulation may be feasible on quantum computers without necessarily requiring scalable, fault-tolerant quantum computers, provided quantum algorithm design incorporates understanding of the materials and applications.

In this work we propose an approach for implementing time-evolution of a quantum system using product formulas. The quantum algorithms we develop have provably better scaling (in terms of gate complexity and circuit depth) than a naive application of well-known Trotter formulas, for systems where the evolution is determined by a Hamiltonian with different energy scales (i.e., one part is "large" and another part is "small"). Our algorithms generate a decomposition of the evolution operator into a product of simple unitaries that are directly implementable on a quantum computer. Although the theoretical scaling is suboptimal compared with state-of-the-art algorithms (e.g., quantum signal processing), the performance of the algorithms we propose is highly competitive in practice. We illustrate this via extensive numerical simulations for several models. For instance, in the strong-field regime of the 1D transverse-field Ising model, our algorithms achieve an improvement of one order of magnitude in both the system size and evolution time that can be simulated with a fixed budget of 1000 arbitrary 2-qubit gates, compared with standard Trotter formulas.

For any local Hamiltonian H, I construct a local CPT map and stopping condition which converges to the ground state subspace of H. Like any ground state preparation algorithm, this algorithm necessarily has exponential run-time in general (otherwise BQP=QMA), even for gapped, frustration-free Hamiltonians (otherwise BQP is in NP). However, this dissipative quantum eigensolver has a number of interesting characteristics, which give advantages over previous ground state preparation algorithms. - The entire algorithm consists simply of iterating the same set of local measurements repeatedly. - The expected overlap with the ground state subspace increases monotonically with the length of time this process is allowed to run. - It converges to the ground state subspace unconditionally, without any assumptions on or prior information about the Hamiltonian. - The algorithm does not require any variational optimisation over parameters. - It is often able to find the ground state in low circuit depth in practice. - It has a simple implementation on certain types of quantum hardware, in particular photonic quantum computers. - The process is immune to errors in the initial state. - It is inherently error- and noise-resilient, i.e. to errors during execution of the algorithm and also to faulty implementation of the algorithm itself, without incurring any computational overhead: the overlap of the output with the ground state subspace degrades smoothly with the error rate, independent of the algorithm's run-time. I give rigorous proofs of the above claims, and benchmark the algorithm on some concrete examples numerically.

Quantum simulations of fermionic many-body systems crucially rely on mappings from indistinguishable fermions to distinguishable qubits. The non-local structure of fermionic Fock space necessitates encodings that either map local fermionic operators to non-local qubit operators, or encode the fermionic representation in a long-range entangled code space. In this latter case, there is an unavoidable trade-off between two desirable properties of the encoding: low weight representations of local fermionic operators, and a high distance code space. Here it is argued that despite this fundamental limitation, fermionic encodings with low-weight representations of local fermionic operators can still exhibit error mitigating properties which can serve a similar role to that played by high code distances. In particular when undetectable errors correspond to "natural" fermionic noise. We illustrate this point explicitly for two fermionic encodings: the Verstraete-Cirac encoding, and an encoding appearing in concurrent work by Derby and Klassen. In these encodings many, but not all, single-qubit errors can be detected. However we show that the remaining undetectable single-qubit errors map to local, low-weight fermionic phase noise. We argue that such noise is natural for fermionic lattice models. This suggests that even when employing low-weight fermionic encodings, error rates can be suppressed in a similar fashion to high distance codes, provided one is willing to accept simulated natural fermionic noise in their simulated fermionic system.

We establish an improved classical algorithm for solving linear systems in a model analogous to the QRAM that is used by quantum linear solvers. Precisely, for the linear system $A\x = \b$, we show that there is a classical algorithm that outputs a data structure for $\x$ allowing sampling and querying to the entries, where $\x$ is such that $\|\x - A^{+}\b\|\leq \epsilon \|A^{+}\b\|$. This output can be viewed as a classical analogue to the output of quantum linear solvers. The complexity of our algorithm is $\widetilde{O}(\kappa_F^4 \kappa^2/\epsilon^2 )$, where$\kappa_F = \|A\|_F\|A^{+}\|$and$\kappa = \|A\|\|A^{+}\|$. This improves the previous best algorithm [Gily{\'e}n, Song and Tang, arXiv:2009.07268] of complexity $\widetilde{O}(\kappa_F^6 \kappa^6/\epsilon^4)$. Our algorithm is based on the randomized Kaczmarz method, which is a particular case of stochastic gradient descent. We also find that when $A$ is row sparse, this method already returns an approximate solution $\x$ in time $\widetilde{O}(\kappa_F^2)$, while the best quantum algorithm known returns $\ket{\x}$ in time $\widetilde{O}(\kappa_F)$ when $A$ is stored in the QRAM data structure. As a result, assuming access to QRAM and if $A$ is row sparse, the speedup based on current quantum algorithms is quadratic.

If classical algorithms have been successful in reproducing the estimation of expectation values of observables of some quantum circuits using off-the-shelf computing resources, matching the performance of the most advanced quantum devices on sampling problems usually requires extreme cost in terms of memory and computing operations, making them accessible to only a handful of supercomputers around the world. In this work, we demonstrate for the first time a classical simulation outperforming Gaussian boson sampling experiments of one hundred modes on established benchmark tests using a single CPU or GPU. Being embarrassingly parallelizable, a small number of CPUs or GPUs allows us to match previous sampling rates that required more than one hundred GPUs. We believe algorithmic and implementation improvements will generalize our tools to photo-counting, single-photon inputs, and pseudo-photon-number-resolving scenarios beyond one thousand modes. Finally, most of the innovations in our tools remain valid for generic probability distributions over binary variables, rendering it potentially applicable to the simulation of qubit-based sampling problems and creating classical surrogates for classical-quantum algorithms.

Mappings between fermions and qubits are valuable constructions in physics. To date only a handful exist. In addition to revealing dualities between fermionic and spin systems, such mappings are indispensable in any quantum simulation of fermionic physics on quantum computers. The number of qubits required per fermionic mode, and the locality of mapped fermionic operators strongly impact the cost of such simulations. We present a novel fermion to qubit mapping which outperforms all previous local mappings in both the qubit to mode ratio, and the locality of mapped operators.

We introduce an algorithm to improve the error scaling of product formulas by randomly sampling the generator of their exact error unitary. Our approach takes an arbitrary product formula of time $t$, $S_k(t)$ with error $O(t^{k+1})$ and produces a stochastic formula with expected error scaling as $O(t^{2k+2})$ with respect to the exact dynamics. For a given fixed error $\epsilon$ and total evolution time $T$ this leads to an improved gate complexity of $N=O(T(T/\epsilon)^{\frac{1}{2k+1}})$ compared to the $O(T(T/\epsilon)^{\frac{1}{k}})$ gate complexity of a $k$-th order product formula. This is achieved by appending an additional circuit with depth at-most logarithmic in the number of qubits, and without needing extra ancillas. We prove that each instance of these stochastic formulas quickly concentrates to the expected value. These results are based on an exact characterization of the error unitaries for product formulas. Through extensive numerical simulations we assess the performance of this approach in several spin and fermionic systems. We show that the expansion of these error unitaries naturally leads to generalized Zassenhaus formulas, a result which could be of independent mathematical interest.

Dissipative processes have long been proposed as a means of performing computational tasks on quantum computers that may be intrinsically more robust to noise. In this work, we prove two main results concerning the error-resilience capabilities of two types of dissipative algorithms: dissipative ground state preparation in the form of the dissipative quantum eigensolver (DQE), and dissipative quantum computation (DQC). The first result is that under circuit-level depolarizing noise, a version of the DQE algorithm applied to the geometrically local, stabilizer-encoded Hamiltonians that arise naturally when fermionic Hamiltonians are represented in qubits, can suppress the additive error in the ground space overlap of the final output state exponentially in the code distance. This enables us to get closer to fault-tolerance for this task without the associated overhead. In contrast, for computation as opposed to ground state preparation, the second result proves that DQC is no more robust to noise than the standard quantum circuit model.