We investigate the joint measurability of incompatible quantum observables on ensembles of parallel and antiparallel spin pairs. In parallel configuration, two systems are identically prepared, whereas in antiparallel configuration each system is paired with its spin-flipped counterpart. We demonstrate that the antiparallel configuration enables exact simultaneous prediction of three mutually orthogonal spin components -- an advantage unattainable in the parallel case. As we show, this enhanced measurement compatibility in antiparallel configuration is better explained within the framework of generalized probabilistic theories, which allow a broader class of composite structures while preserving quantum descriptions at the subsystem level. Furthermore, this approach extends the study of measurement incompatibility to more general configurations beyond just the parallel and antiparallel cases, providing deeper insights into the boundary between physical and unphysical quantum state evolutions. To this end, we discuss how the enhanced measurement compatibility in antiparallel configuration can be observed on a finite ensemble of qubit states, paving the way for an experimental demonstration of this advantage.

Bell nonlocality exemplifies the most profound departure of quantum theory from classical realism. Yet, the extent of nonlocality in quantum theory is intrinsically bounded, falling short of the correlations permitted by the relativistic causality (the no-signaling) principle. A paradigmatic example is the Popescu-Rohrlich correlation: two distant parties sharing arbitrary entanglement cannot achieve this correlation, though it can be simulated with classical communication between them. Here we show how such post-quantum correlations can instead be simulated using intrinsically non-signaling physical resources, and implement the proposed scheme using a quantum circuit on a four-qubit photonic platform. Unlike the conventional approaches, our method exploits dynamical correlations between distinct physical systems, with intrinsic randomness suppressing any signaling capacity. This enables the realization of post-quantum correlations both with and without entanglement. We also analyze how the simulation scheme extends to beyond quantum nonlocal correlations in multipartite systems. Our experimental demonstration using a photonic system establishes a versatile framework for exploring post-quantum correlations in both foundational settings and as a resource for computation and security applications.

The zero-error capacity of a noisy classical channel quantifies its ability to transmit information with absolute certainty, i.e., without any error. Unlike Shannon's standard channel capacity, which remains unaffected by pre-shared correlations, zero-error capacity can be enhanced through nonlocal correlations. In this work, we investigate zero-error communication utility of such correlations arising in the 2-2-m Bell scenario, where two parties have two inputs and m possible outcomes per input. For all m\geq2, we construct examples of noisy classical channels with zero zero-error capacity that, when assisted by extremal 2-2-m nonlocal correlations, can transmit one bit of information. While nonlocal correlations arising from quantum entangled states cannot achieve a positive zero-error capacity for these channels, they significantly enhance the probability of successfully transmitting a classical bit in a single use. Extending this analysis to the 2-m-2 Bell scenario, we identify channels with zero zero-error capacity that can nonetheless perfectly transmit log m bits of information when assisted by corresponding extremal nonlocal correlations. Our findings underscore the versatile utility of Bell nonlocal correlations in achieving zero-error communication.

Quantum nonlocality is usually associated with entangled states by their violations of Bell-type inequalities. However, even unentangled systems, whose parts may have been prepared separately, can show nonlocal properties. In particular, a set of product states is said to exhibit "quantum nonlocality without entanglement" if the states are locally indistinguishable, i.e. it is not possible to optimally distinguish the states by any sequence of local operations and classical communication. Here, we present a stronger manifestation of this kind of nonlocality in multiparty systems through the notion of local irreducibility. A set of multiparty orthogonal quantum states is defined to be locally irreducible if it is not possible to locally eliminate one or more states from the set while preserving orthogonality of the postmeasurement states. Such a set, by definition, is locally indistinguishable, but we show that the converse doesn't always hold. We provide the first examples of orthogonal product bases on $\mathbb{C}^{d}\otimes\mathbb{C}^{d}\otimes\mathbb{C}^{d}$ for $d=3,4$ that are locally irreducible in all bipartitions, where the construction for $d=3$ achieves the minimum dimension necessary for such product states to exist. The existence of such product bases implies that local implementation of a multiparty separable measurement may require entangled resources across all bipartitions.

Transmitting unknown quantum states to distant locations is crucial for distributed quantum information protocols. The seminal quantum teleportation scheme achieves this feat while requiring prior maximal entanglement between the sender and receiver. In scenarios with noisy entangled states, optimal teleportation fidelity characterizes the efficacy of transmitting the state, demanding the proper selection of local operations at the sender's and receiver's ends. The complexity escalates further in long-range communication setups, prompting the consideration of a repeater-based approach, which incorporates arrays of nodes with multiple segments to facilitate the efficient transmission of quantum information. The fidelity of the communication line gets degraded even if a single segment is affected by noise. In such cases, the general wisdom employs the standard entanglement swapping protocol involving maximally entangled states across the noiseless segments and applying maximally entangled basis measurement at the corresponding nodes to achieve optimal fidelity. In this Letter, we propose a more efficient protocol for a certain class of noisy states in any intermediary segment, achieving the same fidelity as the standard protocol while consuming less amount of entanglement. Our approach ensures enhanced teleportation fidelity even when the end-to-end state gets noisier, and thus promises efficient utility of quantum resources in repeater-based distributed quantum protocols.

The destiny of complex organic molecules (COMs) in star-forming regions is interlinked with various evolutionary phases. Therefore, identifying these species in diversified environments of identical star-forming regions would help to comprehend their physical and chemical heritage. We identified multiple COMs utilizing the Large Program `Astrochemical Surveys At IRAM' (ASAI) data, dedicated to chemical surveys in Sun-like star-forming regions with the IRAM 30 m telescope. It was an unbiased survey in the millimetre regime, covering the prestellar core, protostar, outflow region, and protoplanetary disk phase. Here, we have reported some transitions of seven COMs, namely, methanol (CH3OH), acetaldehyde (CH3CHO), methyl formate (CH3OCHO), ethanol (C2H5OH), propynal (HCCCHO), dimethyl ether (CH3OCH3), and methyl cyanide (CH3CN) in some sources L1544, B1-b, IRAS4A, and SVS13A. We found a trend among these species from the derived abundances using the rotational diagram method and MCMC fit. We have found that the abundances of all of the COMs, except for HCCCHO, increase from the L1544 (prestellar core) and peaks at IRAS16293-2422 (class 0 phase). It is noticed that the abundance of these molecules correlate with the luminosity of the sources. The obtained trend is also visible from the previous interferometric observations and considering the beam dilution effect.

The RT-2 Experiment, a low energy gamma-ray telescope, onboard CORONAS-PHOTON satellite is designed to study the temporal, spectral and spatial properties of the hard X-ray solar flares mainly in the energy range of 15 - 100 keV, which is extendable upto 1000 keV. During the operational period of ~ 9 months, it has been able to detect a few solar flares and at least four Gamma-Ray Bursts (GRBs). In this paper, we discuss the properties of the GRBs as observed by RT-2 in the energy band of 15 to ~ 1000 keV. We will present the results of spectral and timing properties of the GRBs (specially for the GRB 090618) using RT-2 detectors. Temporal analysis suggests that all four GRBs belong to the category of long duration bursts.

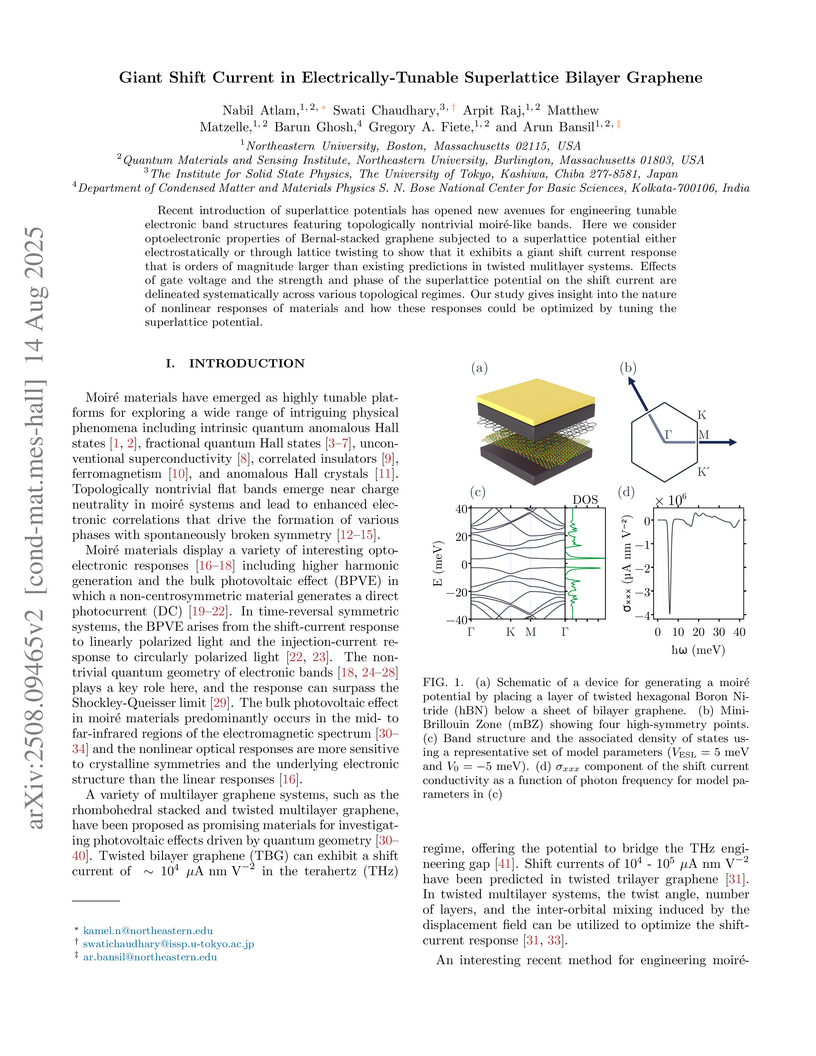
Recent introduction of superlattice potentials has opened new avenues for engineering tunable electronic band structures featuring topologically nontrivial moiré-like bands. Here we consider optoelectronic properties of Bernal-stacked graphene subjected to a superlattice potential either electrostatically or through lattice twisting to show that it exhibits a giant shift current response that is orders of magnitude larger than existing predictions in twisted mulitlayer systems. Effects of gate voltage and the strength and phase of the superlattice potential on the shift current are delineated systematically across various topological regimes. Our study gives insight into the nature of nonlinear responses of materials and how these responses could be optimized by tuning the superlattice potential.

Nonlocality exhibited by ensembles of composite quantum states, wherein local operations and classical communication (LOCC) yield suboptimal discrimination probabilities compared to global strategies, is one of the striking nonclassical features of quantum theory. A variant of this phenomenon arises in conclusive local state discrimination, where the correct state must be identified with zero error, albeit allowing for inconclusive outcomes. More recently, the notion of local state marking has been introduced with the focus shifted to correctly identifying permutation of a subset of states random chosen from a given set of multipartite states under LOCC. In this work, we unify these two approaches by introducing the task of conclusive local state marking, which reveals a finer hierarchy of nonlocality in multipartite quantum state ensembles. Notably, we demonstrate that certain ensembles of product states can exhibit a stronger form of nonlocality than entangled ensembles traditionally considered highly nonlocal.

We study the effect of quantum statistics on the arrival time distribution of quantum particles computed through the probability current density. It is shown that symmetrization or asymmetrization of the wave function affects the arrival time distribution for even freely propagating particles. In order to investigate the effect of statistics on the weak equivalence principle in quantum mechanics (WEQ), we then compute the mean arrival time for wave packets in free fall. The violation of WEQ through the effect of statistics on the mass-dependence of the mean arrival time is clearly exhibited. We finally evaluate the effect of spin on the violation of WEQ using a different approach by including an explicit spin-dependence in the probability current distribution, and compare it with the approach using particle statistics. Our results show WEQ re-emerges smoothly in the limit of large mass.

Discrimination of quantum states under local operations and classical communication (LOCC) is an intriguing question in the context of local retrieval of classical information, encoded in the multipartite quantum systems. All the local quantum state discrimination premises, considered so far, mimic a basic communication set-up, where the spatially separated decoding devices are independent of any additional input. Here, exploring a generalized communication scenario we introduce a framework for input-dependent local quantum state discrimination, which we call local random authentication (LRA). Referring to the term nonlocality, often used to indicate the impossibility of local state discrimination, we coin the term conditional nonlocality for the impossibility associated with the task LRA. We report that conditional nonlocality necessitates the presence of entangled states in the ensemble, a feature absent from erstwhile nonlocality arguments based on local state discrimination. Conversely, all the states in a complete basis set being entangled implies conditional nonlocality. However, the impossibility of LRA also exhibits more conditional nonlocality with less entanglement. The relation between the possibility of LRA and local state discrimination for sets of multipartite quantum states, both in the perfect and conclusive cases, has also been established. The results highlight a completely new aspect of the interplay between the security of information in a network and quantum entanglement under the LOCC paradigm.

It is known from density functional theory (DFT) calculations that RhSi has a multifold degenerate Dirac point at the Fermi energy, with the dominant states in the low-energy region displaying mostly Rh $d$ character. Using DFT+U, we calculate the band structure by considering an effective local interaction on the Rh $d$ states, with a realistic effective Hubbard $U_\textrm{eff}=2.5$ eV derived from a constrained random-phase approximation calculation, and find the emergence of a double hump structure close to the Fermi this http URL further deriving a low-energy tight-binding model from our first-principles results, we show that the double hump is a direct consequence of a competition between the Rh $d$-Rh $d$ and Rh $d$-Si $p$ interactions, which differ in their momentum dependence. As a consequence, through an artificial tuning of the energy level of the Si $p$ orbitals this hump structure can be suppressed due to the effectively reduced Rh $d$ -Si $p$ this http URL peculiar low-energy electronic structure additionally results in that a small hole/electron doping ($\sim$ 0.1 $\%$) can tune the Fermi surface topology, going from closed to open Fermi surfaces, which has dramatic consequences for the thermal transport.

In a startling discovery it has been recently found that certain density of states (DOS) can become negative in mesoscopic systems wherein electrons can travel back in time. We give a brief introduction to the hierarchy of density of states in mesoscopic systems as we want to point out some robust phenomenon that can be experimentally observed with our present day technologies. They can have direct consequences on thermodynamic effects and also can provide indirect evidence of time travel. Essentially certain members of the hierarchy of DOS become negative in these regimes and that can attract other electrons.

Claude Shannon's zero-error communication paradigm reshaped our understanding of fault-tolerant information transfer. Here, we adapt this notion into game theory with incomplete information. We ask: can players with private information coordinate on a Nash equilibrium with zero probability of error? We identify Bayesian games in which such coordination is impossible classically, yet achievable by harnessing Bell nonlocal correlations. We formalize this requirement as zero-error Nash equilibrium coordination, establishing a new bridge between information theory, game theory, and quantum nonlocality. Furthermore, we construct a tripartite Bayesian game that admits zero-error Nash equilibrium coordination with genuine entanglement, and a two-player game where a stronger notion of coordination can be achieved using every two-qubit pure entangled state except the maximally one. Crucially, the advantage persists under experimentally relevant noise, demonstrating nonlocality as a robust resource for near-zero error decision-making under uncertainty.

The mathematical framework of quantum theory, though fundamentally distinct from classical physics, raises the question of whether quantum processes can be efficiently simulated using classical resources. For instance, a sender (Alice) possessing the classical description of a qubit state can simulate the action of a qubit channel through finite classical communication with a receiver (Bob), enabling Bob to reproduce measurement statistics for any observable on the state. In this work, we contend that a more general simulation requires reproducing statistics of joint measurements, potentially involving entangled effects, on Alice's system and an additional system held by Bob, even when Bob's system state is unknown or entangled with a larger system. Within this broad framework, we prove that no finite amount of classical messaging, regardless of how many rounds are used or how large each message can be, can reproduce a perfect qubit channel, highlighting an inescapable barrier in quantum channel simulation with classical resources. We also establish that entangled effects crucially underlies this no-go result. However, for noisy qubit channels, such as those with depolarizing noise, we demonstrate that general simulation is achievable with finite communication. Notably, the required communication increases as the noise decreases, revealing an intricate relationship between the noise in the channel and the resources necessary for its classical simulation.

The weak equivalence principle of gravity is examined at the quantum level in two ways. First, the position detection probabilities of particles described by a non-Gaussian wave-packet projected upwards against gravity around the classical turning point and also around the point of initial projection are calculated. These probabilities exhibit mass-dependence at both these points, thereby reflecting the quantum violation of the weak equivalence principle. Secondly, the mean arrival time of freely falling particles is calculated using the quantum probability current, which also turns out to be mass dependent. Such a mass-dependence is shown to be enhanced by increasing the non-Gaussianity parameter of the wave packet, thus signifying a stronger violation of the weak equivalence principle through a greater departure from Gaussianity of the initial wave packet. The mass-dependence of both the position detection probabilities and the mean arrival time vanish in the limit of large mass. Thus, compatibility between the weak equivalence principle and quantum mechanics is recovered in the macroscopic limit of the latter. A selection of Bohm trajectories is exhibited to illustrate these features in the free fall case.

The quantum switch describes a quantum operation in which two or more quantum channels act on a quantum system with the order of application determined by the state of an order quantum system. And by suitably choosing the state of the order system, one can create a quantum superposition of the different orders of application, which can perform communication tasks impossible within the framework of the standard quantum Shannon theory. In this paper, we consider the scenario of one-shot heralded qubit communication and ask whether there exist protocols using a given quantum switch or switches that could outperform the given ones. We answer this question in the affirmative. We define a higher-order quantum switch composed of two quantum switches, with their order of application controlled by another order quantum system. We then show that the quantum switches placed in a quantum superposition of their alternative orders can transmit a qubit, without any error, with a probability higher than that achievable with the quantum switches individually. We demonstrate this communication advantage over quantum switches useful as a resource and those that are useless. We also show that there are situations where there is no communication advantage over the individual quantum switches.

A fundamental limitation of quantum communication is that a single qubit can carry at most 1 bit of classical information. For an important class of quantum communication channels, known as entanglement-breaking, this limitation holds even if the sender and receiver share entangled particles. But does this mean that, for the purpose of communicating classical messages, a noisy entanglement-breaking qubit channel can be replaced by a noisy bit channel? Here we answer the question in the negative. We introduce a game, similar to the Monty Hall problem in classical statistics, where a sender assists a receiver in finding a valuable item (the prize) hidden into one of four possible boxes, while avoiding a hazardous item (the bomb) hidden in one of the remaining three boxes. We show that no classical strategy using a noisy bit channel can ensure that the bomb is avoided, even if the sender and receiver share arbitrary amounts of randomness. In contrast, communication of a qubit through a class of noisy entanglement-breaking channels, which we call quantum NOT channels, allows the players to deterministically avoid the bomb and to find the prize with a guaranteed nonzero probability. Our findings show that the communication of classical messages through a noisy entanglement-breaking qubit channel assisted by quantum entanglement cannot, in general, be simulated by communication through a noisy bit channel assisted by classical correlations.

Nonclassicality in composite quantum systems depicts several puzzling manifestations, with Einstein-Podolsky-Rosen entanglement, Schr\"odinger steering, and Bell nonlocality being the most celebrated ones. In addition to those, an unentangled quantum state can also exhibit nonclassicality, as evidenced from notions such as quantum discord and work deficit. Here, we propose a general framework to investigate nonclassical correlations in multipartite quantum states. The distinct signatures left on observable quantities, depending on whether the sub-parts of a composite system are probed separately or jointly, provide an operational avenue to construct different quantifiers that faithfully capture signatures of nonclassicality in quantum states. Along the line we unveil an intriguing phenomenon referred to as `nonlocal locking of observable quantities', where the value of an observable quantity gets locked in the correlation of a nonclassical state. Our approach reduces the experimental demand for verification of nonclassicality in composite systems and can find applications for enhanced energy storage in quantum thermodynamical devices.