This paper introduces torchsom, an open-source Python library that provides a reference implementation of the Self-Organizing Map (SOM) in PyTorch. This package offers three main features: (i) dimensionality reduction, (ii) clustering, and (iii) friendly data visualization. It relies on a PyTorch backend, enabling (i) fast and efficient training of SOMs through GPU acceleration, and (ii) easy and scalable integrations with PyTorch ecosystem. Moreover, torchsom follows the scikit-learn API for ease of use and extensibility. The library is released under the Apache 2.0 license with 90% test coverage, and its source code and documentation are available at this https URL.

We consider the problem of uncertainty quantification in high dimensional regression and classification for which deep ensemble have proven to be promising methods. Recent observations have shown that deep ensemble often return overconfident estimates outside the training domain, which is a major limitation because shifted distributions are often encountered in real-life scenarios. The principal challenge for this problem is to solve the trade-off between increasing the diversity of the ensemble outputs and making accurate in-distribution predictions. In this work, we show that an ensemble of networks with large weights fitting the training data are likely to meet these two objectives. We derive a simple and practical approach to produce such ensembles, based on an original anti-regularization term penalizing small weights and a control process of the weight increase which maintains the in-distribution loss under an acceptable threshold. The developed approach does not require any out-of-distribution training data neither any trade-off hyper-parameter calibration. We derive a theoretical framework for this approach and show that the proposed optimization can be seen as a "water-filling" problem. Several experiments in both regression and classification settings highlight that Deep Anti-Regularized Ensembles (DARE) significantly improve uncertainty quantification outside the training domain in comparison to recent deep ensembles and out-of-distribution detection methods. All the conducted experiments are reproducible and the source code is available at \url{this https URL}.

This paper deals with uncertainty quantification and out-of-distribution detection in deep learning using Bayesian and ensemble methods. It proposes a practical solution to the lack of prediction diversity observed recently for standard approaches when used out-of-distribution (Ovadia et al., 2019; Liu et al., 2021). Considering that this issue is mainly related to a lack of weight diversity, we claim that standard methods sample in "over-restricted" regions of the weight space due to the use of "over-regularization" processes, such as weight decay and zero-mean centered Gaussian priors. We propose to solve the problem by adopting the maximum entropy principle for the weight distribution, with the underlying idea to maximize the weight diversity. Under this paradigm, the epistemic uncertainty is described by the weight distribution of maximal entropy that produces neural networks "consistent" with the training observations. Considering stochastic neural networks, a practical optimization is derived to build such a distribution, defined as a trade-off between the average empirical risk and the weight distribution entropy. We develop a novel weight parameterization for the stochastic model, based on the singular value decomposition of the neural network's hidden representations, which enables a large increase of the weight entropy for a small empirical risk penalization. We provide both theoretical and numerical results to assess the efficiency of the approach. In particular, the proposed algorithm appears in the top three best methods in all configurations of an extensive out-of-distribution detection benchmark including more than thirty competitors.

The goal of the paper is to design active learning strategies which lead to domain adaptation under an assumption of Lipschitz functions. Building on previous work by Mansour et al. (2009) we adapt the concept of discrepancy distance between source and target distributions to restrict the maximization over the hypothesis class to a localized class of functions which are performing accurate labeling on the source domain. We derive generalization error bounds for such active learning strategies in terms of Rademacher average and localized discrepancy for general loss functions which satisfy a regularity condition. A practical K-medoids algorithm that can address the case of large data set is inferred from the theoretical bounds. Our numerical experiments show that the proposed algorithm is competitive against other state-of-the-art active learning techniques in the context of domain adaptation, in particular on large data sets of around one hundred thousand images.

The main goal of this work is to develop a data-driven Reduced Order Model (ROM) strategy from high-fidelity simulation result data of a Full Order Model (FOM). The goal is to predict at lower computational cost the time evolution of solutions of Fluid-Structure Interaction (FSI) problems. For some FSI applications, the elastic solid FOM (often chosen as quasi-static) can take far more computational time than the fluid one. In this context, for the sake of performance one could only derive a ROM for the structure and try to achieve a partitioned FOM fluid solver coupled with a ROM solid one. In this paper, we present a data-driven partitioned ROM on two study cases: (i) a simplified 1D-1D FSI problem representing an axisymmetric elastic model of an arterial vessel, coupled with an incompressible fluid flow; (ii) an incompressible 2D wake flow over a cylinder facing an elastic solid with two flaps. We evaluate the accuracy and performance of the proposed ROM-FOM strategy on these cases while investigating the effects of the model's hyperparameters. We demonstrate a high prediction accuracy and significant speedup achievements using this strategy.

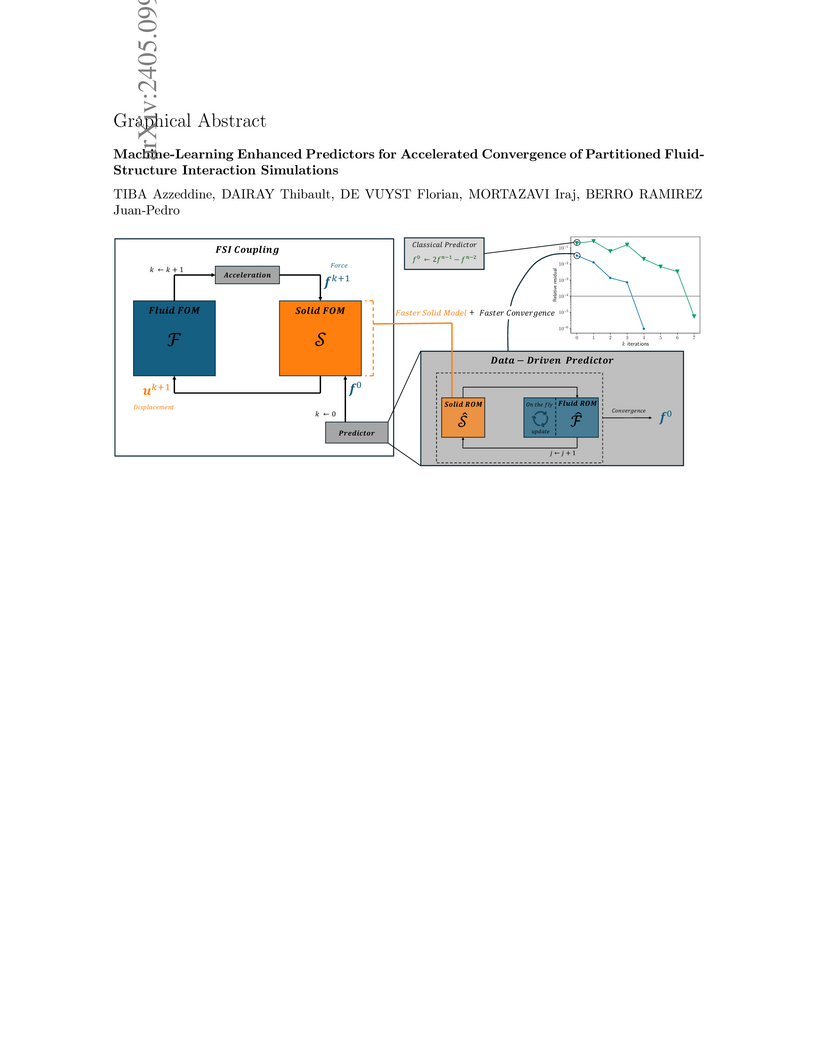
Stable partitioned techniques for simulating unsteady fluid-structure interaction (FSI) are known to be computationally expensive when high added-mass is involved. Multiple coupling strategies have been developed to accelerate these simulations, but often use predictors in the form of simple finite-difference extrapolations. In this work, we propose a non-intrusive data-driven predictor that couples reduced-order models of both the solid and fluid subproblems, providing an initial guess for the nonlinear problem of the next time step calculation. Each reduced order model is composed of a nonlinear encoder-regressor-decoder architecture and is equipped with an adaptive update strategy that adds robustness for extrapolation. In doing so, the proposed methodology leverages physics-based insights from high-fidelity solvers, thus establishing a physics-aware machine learning predictor. Using three strongly coupled FSI examples, this study demonstrates the improved convergence obtained with the new predictor and the overall computational speedup realized compared to classical approaches.