Recent advances in quantum technologies have enabled quantum simulation of gauge theories -- some of the most fundamental frameworks of nature -- in regimes far from equilibrium, where classical computation is severely limited. These simulators, primarily based on neutral atoms, trapped ions, and superconducting circuits, hold the potential to address long-standing questions in nuclear, high-energy, and condensed-matter physics, and may ultimately allow first-principles studies of matter evolution in settings ranging from the early universe to high-energy collisions. Research in this rapidly growing field is also driving the convergence of concepts across disciplines and uncovering new phenomena. In this Review, we highlight recent experimental and theoretical developments, focusing on phenomena accessible in current and near-term quantum simulators, including particle production and string breaking, collision dynamics, thermalization, ergodicity breaking, and dynamical quantum phase transitions. We conclude by outlining promising directions for future research and opportunities enabled by available quantum hardware.

We study modular theory in hyperfinite von Neumann algebras, i.e. in those of type II or type III, from the viewpoint of a subregion charge sector decomposition. We address this symmetry resolution by considering infinite tensor products of finite-dimensional algebras with fixed subregion charge values. An important ingredient is the combination of these algebras using direct integrals. This allows us to obtain the symmetry-resolved modular operator, modular flow, and modular correlation functions for hyperfinite algebras. Our approach establishes a mathematical foundation for recent results on symmetry resolution and modular theory in conformal field theory. Our analysis applies both to charges defined on a continuous range, or on a discrete set. The latter is of interest for condensed matter theory. Moreover, within the AdS/CFT correspondence we expect our findings to be relevant as a new ingredient for bulk spacetime reconstruction, including information from different boundary charge sectors.

We present a quantum simulation framework universally applicable to a wide class of quantum systems, including quantum field theories such as quantum chromodynamics (QCD). Specifically, we generalize an efficient quantum simulation protocol developed for bosonic theories in [Halimeh et al., arXiv:2411.13161] which, when applied to Yang-Mills theory, demonstrated an exponential resource advantage with respect to the truncation level of the bosonic modes, to systems with both bosons and fermions using the Jordan-Wigner transform and also the Verstraete-Cirac transform. We apply this framework to QCD using the orbifold lattice formulation and achieve an exponential speedup compared to previous proposals. As a by-product, exponential speedup is achieved in the quantum simulation of the Kogut-Susskind Hamiltonian, the latter being a special limit of the orbifold lattice Hamiltonian. In the case of Hamiltonian time evolution of a theory on an $L^d$ spatial lattice via Trotterization, one Trotter step can be realized using $\mathcal{O}(L^d)$ numbers of CNOT gates, Hadamard gates, phase gates, and one-qubit rotations. We show this analytically for any matter content and $\mathrm{SU}(N)$ gauge group with any $N$. Even when we use the Jordan-Wigner transform, we can utilize the cancellation of quantum gates to significantly simplify the quantum circuit. We also discuss a block encoding of the Hamiltonian as a linear combination of unitaries using the Verstraete-Cirac transform. Our protocols do not assume oracles, but rather present explicit constructions with rigorous resource estimations without a hidden cost, and are thus readily implementable on a quantum computer.

Parton distribution functions (PDFs) describe the inner, non-perturbative structure of hadrons. Their computation involves matrix elements with a Wilson line along a direction on the light cone, posing significant challenges in Euclidean lattice calculations, where the time direction is not directly accessible. We propose implementing the light-front Wilson line within the Hamiltonian formalism using tensor network techniques. The approach is demonstrated in the massive Schwinger model (quantum electrodynamics in 1+1 dimensions), a toy model that shares key features with quantum chromodynamics. We present accurate continuum results for the fermion PDF of the vector meson at varying fermion masses, obtained from first principle calculations directly in Minkowski space. Our strategy also provides a useful path for quantum simulations and quantum computing.

We test the eigenstate thermalization hypothesis (ETH) in 1+1-dimensional SU(2) lattice gauge theory (LGT) with one flavor of dynamical fermions. Using the loop-string-hadron framework of the LGT with a bosonic cut-off, we exactly diagonalize the Hamiltonian for finite size systems and calculate matrix elements (MEs) in the eigenbasis for both local and non-local operators. We analyze different indicators to identify the parameter space for quantum chaos at finite lattice sizes and investigate how the ETH behavior emerges in both the diagonal and off-diagonal MEs. Our investigations allow us to study various time scales of thermalization and the emergence of random matrix behavior, and highlight the interplays of the several diagnostics with each other. Furthermore, from the off-diagonal MEs, we extract a smooth function that is closely related to the spectral function for both local and non-local operators. We find numerical evidence of the spectral gap and the memory peak in the non-local operator case. Finally, we investigate aspects of subsystem ETH in the lattice gauge theory and identify certain features in the subsystem reduced density matrix that are unique to gauge theories.

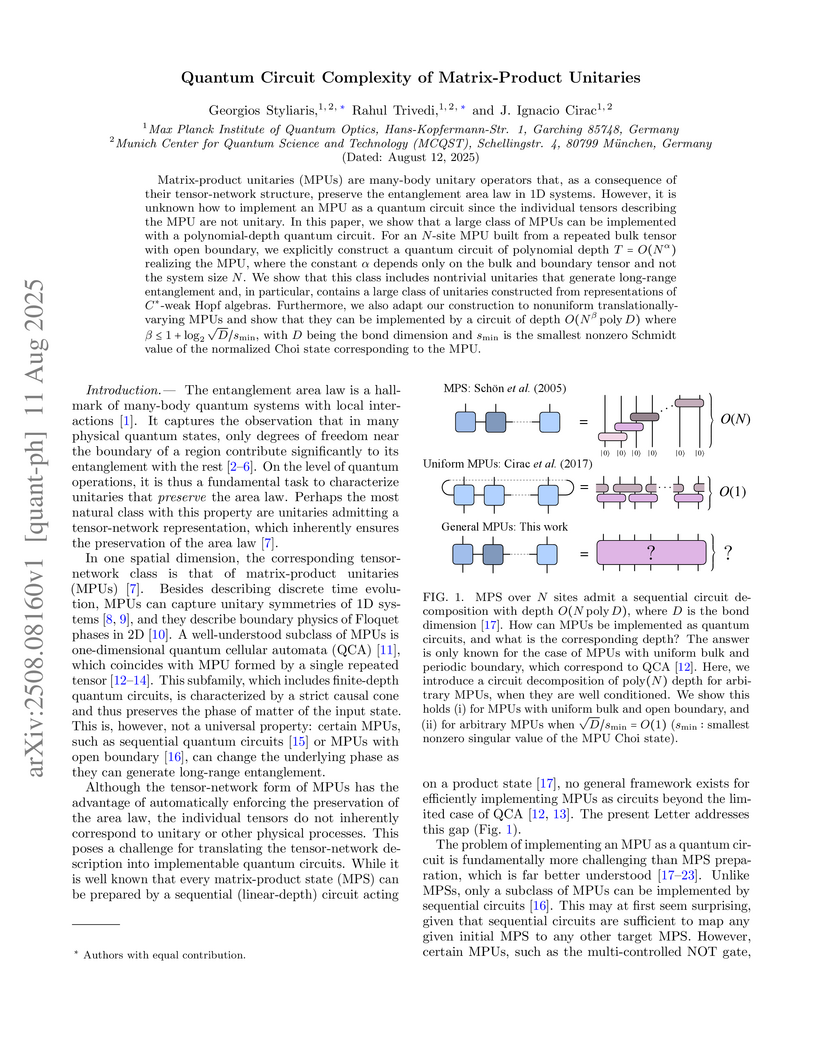
Matrix-product unitaries (MPUs) are many-body unitary operators that, as a consequence of their tensor-network structure, preserve the entanglement area law in 1D systems. However, it is unknown how to implement an MPU as a quantum circuit since the individual tensors describing the MPU are not unitary. In this paper, we show that a large class of MPUs can be implemented with a polynomial-depth quantum circuit. For an $N$-site MPU built from a repeated bulk tensor with open boundary, we explicitly construct a quantum circuit of polynomial depth $T = O(N^{\alpha})$ realizing the MPU, where the constant $\alpha$ depends only on the bulk and boundary tensor and not the system size $N$. We show that this class includes nontrivial unitaries that generate long-range entanglement and, in particular, contains a large class of unitaries constructed from representations of $C^*$-weak Hopf algebras. Furthermore, we also adapt our construction to nonuniform translationally-varying MPUs and show that they can be implemented by a circuit of depth $O(N^{\beta} \, \mathrm{poly}\, D)$ where $\beta \le 1 + \log_2 \sqrt{D}/ s_{\min}$, with $D$ being the bond dimension and $s_{\min}$ is the smallest nonzero Schmidt value of the normalized Choi state corresponding to the MPU.

We show how to optimally reduce the local Hilbert basis of lattice quantum many-body (QMB) Hamiltonians. The basis truncation exploits the most relevant eigenvalues of the estimated single-site reduced density matrix (RDM). It is accurate and numerically stable across different model phases, even close to quantum phase transitions. We apply this procedure to different models, such as the Sine-Gordon model, the $\varphi^{4}$ theory, and lattice gauge theories, namely Abelian $\mathrm{U}(1)$ and non-Abelian $\mathrm{SU}(2)$, in one and two spatial dimensions. Our results reduce state-of-the-art estimates of computational resources for classical and quantum simulations.

We provide a universal framework for the quantum simulation of SU(N) Yang--Mills theories on fault-tolerant digital quantum computers adopting the orbifold lattice formulation. As warm-up examples, we also consider simple models, including scalar field theory and the Yang--Mills matrix model, to illustrate the universality of our formulation, which shows up in the fact that the truncated Hamiltonian can be expressed in the same simple form for any N, any dimension, and any lattice size, in stark contrast to the popular approach based on the Kogut--Susskind formulation. In all these cases, the truncated Hamiltonian can be programmed on a quantum computer using only standard tools well-established in the field of quantum computation. As a concrete application of this universal framework, we consider Hamiltonian time evolution by Suzuki--Trotter decomposition. This turns out to be a straightforward task due to the simplicity of the truncated Hamiltonian. We also provide a simple circuit structure that contains only CNOT and one-qubit gates, independent of the details of the theory investigated.

We investigate the time dependence of anti-flatness in the entanglement spectrum, a measure for non-stabilizerness and lower bound for non-local quantum magic, on a subsystem of a linear SU(2) plaquette chain during thermalization. Tracing the time evolution of a large number of initial states, we find that the anti-flatness exhibits a barrier-like maximum during the time period when the entanglement entropy of the subsystem grows rapidly from the initial value to the microcanonical entropy. The location of the peak is strongly correlated with the time when the entanglement exhibits the strongest growth. This behavior is found for generic highly excited initial computational basis states and persists for coupling constants across the ergodic regime, revealing a universal structure of the entanglement spectrum during thermalization. We conclude that quantitative simulations of thermalization for nonabelian gauge theories require quantum computing. We speculate that this property generalizes to other quantum chaotic systems.

Understanding flux string dynamics can provide insight into quark confinement and hadronization. First-principles quantum and numerical simulations have mostly focused on toy-model Abelian lattice gauge theories (LGTs). With the advent of state-of-the-art quantum simulation experiments, it is important to bridge this gap and study string dynamics in non-Abelian LGTs beyond one spatial dimension. Using tensor network methods, we simulate the real-time string dynamics of a $2\!+\!1$D SU$(2)$ Yang--Mills LGT with dynamical matter. In the strong-coupling regime and at resonance, string breaking occurs through sharp Casimir reduction along with meson and baryon-antibaryon formation, a distinctively non-Abelian feature. At finite baryon density, we discover a \textit{baryon blockade} mechanism that delays string breaking. Away from resonance, the magnetic term drives purely non-Abelian fluctuations: glueball loops and self-crossed strings that resolve two SU$(2)$ intertwiners with distinct dynamics. For higher-energy strings, we uncover representation-dependent tension-reduction resonances. Our findings serve as a guide for upcoming quantum simulators of non-Abelian LGTs.

We present a quantum process tomography protocol based on a low-degree ansatz for the quantum channel, i.e. when it can be expressed as a fixed-degree polynomial in terms of Pauli operators. We demonstrate how to perform tomography of such channels with a polynomial amount of effort relative to the size of the system, by employing random state preparation and measurements in the Pauli basis. We extend the applicability of the protocol to channels consisting of a layer of quantum gates with a fixed number of non-Clifford gates, followed by a low-degree noise channel. Rather than inverting the layer of quantum gates in the hardware, which would introduce new errors, we effectively carry out the inversion by classical post-processing while maintaining the protocol's efficiency. Numerical simulations support our theoretical findings and demonstrate the feasibility of our method.

\usepackage{iopams} Recent developments have revealed that symmetries need not form a group, but instead can be non-invertible. Here we use analytical arguments and numerical evidence to illuminate how spontaneous symmetry breaking of a non-invertible symmetry is similar yet distinct from ordinary, invertible, symmetry breaking. We consider one-dimensional chains of group-valued qudits, whose local Hilbert space is spanned by elements of a finite group $G$ (reducing to ordinary qubits when $G=\mathbb{Z}_2$). We construct Ising-type transverse-field Hamiltonians with Rep($G$) symmetry whose generators multiply according to the tensor product of irreducible representations (irreps) of the group $G$. For non-Abelian $G$, the symmetry is non-invertible. In the symmetry broken phase there is one ground state per irrep on a closed chain. The symmetry breaking can be detected by local order parameters but, unlike the invertible case, different ground states have distinct entanglement patterns. We show that for each irrep of dimension greater than one the corresponding ground state exhibits string order, entanglement spectrum degeneracies, and has gapless edge modes on an open chain -- features usually associated with symmetry-protected topological order. Consequently, domain wall excitations behave as one-dimensional non-Abelian anyons with non-trivial internal Hilbert spaces and fusion rules. Our work identifies properties of non-invertible symmetry breaking that existing quantum hardware can probe.

Universal aspects of thermalization in interacting many-body systems are typically challenging to derive microscopically, yet provide a powerful framework for understanding emergent phenomena. Here, we numerically study the mean-field dynamics of a $(2+1)$D spin system with thousands of spins and show that experimentally-feasible two-body Ising interactions can stabilize a prethermal $\mathbb{Z}_2$ lattice gauge structure with dynamical matter, manifested by a gauge-invariant plateau with exponentially long lifetime. Eventually, the metastable prethermal $\mathbb{Z}_2$ gauge structure breaks down via a proliferation of Gauss' law defects, similar to bubble formation in false vacuum decay. In this regime, we discover spatio-temporal correlations described by a non-linear surface growth consistent with the $(1+1)$D Kardar-Parisi-Zhang (KPZ) universality class. We benchmark our results in small systems against semi-classical discrete time Wigner approximation (DTWA) and exact diagonalization (ED), where the breakdown of DTWA signals the emergence of an extensive number of local symmetries that strongly influence the thermalization pathway. Our model provides a testbed for quantum simulators and is directly implementable in large-scale arrays of Rydberg atoms.

We present and test a protocol to learn the matrix-product operator (MPO) representation of an experimentally prepared quantum state. The protocol takes as an input classical shadows corresponding to local randomized measurements, and outputs the tensors of a MPO which maximizes a suitably-defined fidelity with the experimental state. The tensor optimization is carried out sequentially, similarly to the well-known density matrix renormalization group algorithm. Our approach is provably efficient under certain technical conditions which are expected to be met in short-range correlated states and in typical noisy experimental settings. Under the same conditions, we also provide an efficient scheme to estimate fidelities between the learned and the experimental states. We experimentally demonstrate our protocol by learning entangled quantum states of up to $N = 96$ qubits in a superconducting quantum processor. Our method upgrades classical shadows to large-scale quantum computation and simulation experiments.

We demonstrate deterministic preparation of arbitrary two-component product states of fermionic $^6$Li atoms in an 8$\times$8 optical tweezer array, achieving motional ground-state fidelities above 98.5\%. Leveraging the large differential magnetic moments for spin-resolution, with parallelized site- and number-resolved control, our approach addresses key challenges for low-entropy quantum state engineering. Combined with high-fidelity spin-, site-, and density-resolved readout within a single \qty{20}{\us} exposure, and \qty{3}{\s} experimental cycles, these advances establish a fast, scalable, and programmable architecture for fermionic quantum simulation.

Matrix Product Operators (MPOs) are tensor networks representing operators acting on 1D systems. They model a wide variety of situations, including communication channels with memory effects, quantum cellular automata, mixed states in 1D quantum systems, or holographic boundary models associated to 2D quantum systems. A scenario where MPOs have proven particularly useful is to represent algebras of non-trivial symmetries. Concretely, the boundary of both symmetry protected and topologically ordered phases in 2D quantum systems exhibit symmetries in the form of MPOs. In this paper, we develop a theory of MPOs as representations of algebraic structures. We establish a dictionary between algebra and MPO properties which allows to transfer results between both setups, covering the cases of pre-bialgebras, weak bialgebras, and weak Hopf algebras. We define the notion of pulling-through algebras, which abstracts the minimal requirements needed to define topologically ordered 2D tensor networks from MPO algebras. We show, as one of our main results, that any semisimple pivotal weak Hopf algebra is a pulling-trough algebra. We demonstrate the power of this framework by showing that they can be used to construct Kitaev's quantum double models for Hopf algebras solely from an MPO representation of the Hopf algebra, in the exact same way as MPO symmetries obtained from fusion categories can be used to construct Levin-Wen string-net models, and to explain all their topological features; it thus allows to describe both Kitaev and string-net models on the same formal footing.

Drawing independent samples from a probability distribution is an important computational problem with applications in Monte Carlo algorithms, machine learning, and statistical physics. The problem can in principle be solved on a quantum computer by preparing a quantum state that encodes the entire probability distribution followed by a projective measurement. We investigate the complexity of adiabatically preparing such quantum states for the Gibbs distributions of various classical models including the Ising chain, hard-sphere models on different graphs, and a model encoding the unstructured search problem. By constructing a parent Hamiltonian, whose ground state is the desired quantum state, we relate the asymptotic scaling of the state preparation time to the nature of transitions between distinct quantum phases. These insights enable us to identify adiabatic paths that achieve a quantum speedup over classical Markov chain algorithms. In addition, we show that parent Hamiltonians for the problem of sampling from independent sets on certain graphs can be naturally realized with neutral atoms interacting via highly excited Rydberg states.

Simulating quantum dynamics on digital or analog quantum simulators often requires ``problem-to-simulator" mappings such as trotterization, floquet-magnus expansion or perturbative expansions. When the simulator is noiseless, it is well understood that these problem-to-simulator mappings can be made as accurate as desired at the expense of simulator run-time. However, precisely because the simulator has to be run for a longer time to increase its accuracy, it is expected that noise in the quantum simulator catastrophically effects the simulator output. We show that, contrary to this expectation, these mappings remain stable to noise when considering the task of simulating dynamics of local observables in quantum lattice models. Specifically, we prove that in all of these mappings, local observables can be determined to a system-size independent, precision that scales sublinearly with the noise-rate in the simulator. Our results provide theoretical evidence that quantum simulators can be used for solving problems in many-body physics without or with modest error correction.

Despite recent advances in the lattice representation theory of (generalized) symmetries, many simple quantum spin chains of physical interest are not included in the rigid framework of fusion categories and weak Hopf algebras. We demonstrate that this problem can be overcome by relaxing the requirements on the underlying algebraic structure, and show that general matrix product operator symmetries are described by a pre-bialgebra. As a guiding example, we focus on the anomalous $\mathbb Z_2$ symmetry of the XX model, which manifests the mixed anomaly between its $U(1)$ momentum and winding symmetry. We show how this anomaly is embedded into the non-semisimple corepresentation category, providing a novel mechanism for realizing such anomalous symmetries on the lattice. Additionally, the representation category which describes the renormalization properties is semisimple and semi-monoidal, which provides a new class of mixed state renormalization fixed points. Finally, we show that up to a quantum channel, this anomalous $\mathbb Z_2$ symmetry is equivalent to a more conventional MPO symmetry obtained on the boundary of a double semion model. In this way, our work provides a bridge between well-understood topological defect symmetries and those that arise in more realistic models.

We study Projected Entangled Pair States (PEPS) with continuous virtual symmetries, i.e., symmetries in the virtual degrees of freedom, through an elementary class of models with SU(2) symmetry. Discrete symmetries of that kind have previously allowed for a comprehensive explanation of topological order in the PEPS formalism. We construct local parent Hamiltonians whose ground space with open boundaries is exactly parametrized by the PEPS wavefunction, and show how the ground state can be made unique by a suitable choice of boundary conditions. We also find that these models exhibit a logarithmic correction to the entanglement entropy and an extensive ground space degeneracy on systems with periodic boundaries, which suggests that they do not describe conventional gapped topological phases, but either critical models or some other exotic phase.