The parquet decomposition of the self-energy into classes of diagrams, those associated with specific scattering processes, can be exploited for different scopes. In this work, the parquet decomposition is used to unravel the underlying physics of non-perturbative numerical calculations. We show the specific example of dynamical mean field theory (DMFT) and its cluster extensions (DCA) applied to the Hubbard model at half-filling and with hole doping: These techniques allow for a simultaneous determination of two-particle vertex functions and self-energies, and hence, for an essentially "exact" parquet decomposition at the single-site or at the cluster level. Our calculations show that the self-energies in the underdoped regime are dominated by spin scattering processes, consistent with the conclusions obtained by means of the fluctuation diagnostics approach [Phys. Rev. Lett. 114, 236402 (2015)]. However, differently from the latter approach, the parquet procedure displays important changes with increasing interaction: Even for relatively moderate couplings, well before the Mott transition, singularities appear in different terms, with the notable exception of the predominant spin-channel. We explain precisely how these singularities, which partly limit the utility of the parquet decomposition, and - more generally - of parquet-based algorithms, are never found in the fluctuation diagnostics procedure. Finally, by a more refined analysis, we link the occurrence of the parquet singularities in our calculations to a progressive suppression of charge fluctuations and the formation of an RVB state, which are typical hallmarks of a pseudogap state in DCA.

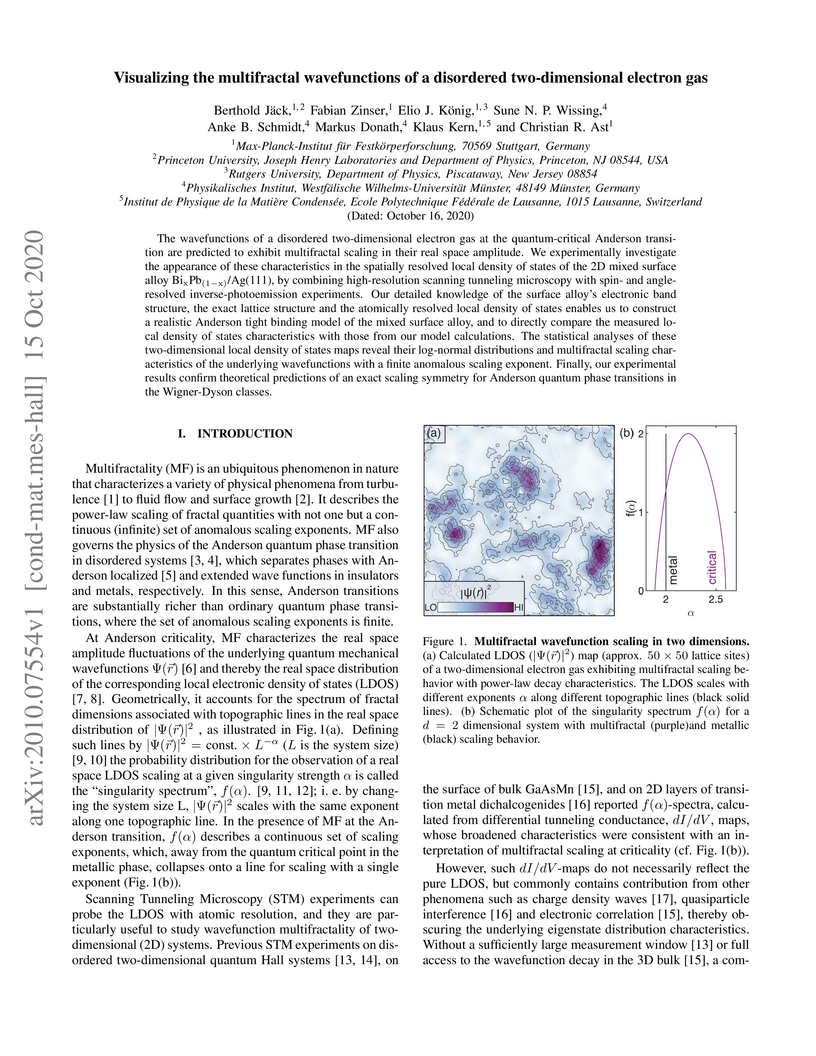
The wavefunctions of a disordered two-dimensional electron gas at the quantum-critical Anderson transition are predicted to exhibit multifractal scaling in their real space amplitude. We experimentally investigate the appearance of these characteristics in the spatially resolved local density of states of a two-dimensional mixed surface alloy Bi_xPb_{1-x}/Ag(111), by combining high-resolution scanning tunneling microscopy with spin and angle-resolved inverse-photoemission experiments. Our detailed knowledge of the surface alloy electronic band structure, the exact lattice structure and the atomically resolved local density of states enables us to construct a realistic Anderson tight binding model of the mixed surface alloy, and to directly compare the measured local density of states characteristics with those from our model calculations. The statistical analyses of these two-dimensional local density of states maps reveal their log-normal distributions and multifractal scaling characteristics of the underlying wavefunctions with a finite anomalous scaling exponent. Finally, our experimental results confirm theoretical predictions of an exact scaling symmetry for Anderson quantum phase transitions in the Wigner-Dyson classes.

From first-principles calculations, we investigate the structural and electronic properties of the kagome metals AV3Sb5 (A = Cs, K, Rb) under isotropic and anisotropic pressure. Charge ordering patterns are found to be unanimously suppressed, while there is a significant rearrangement of p-type and m-type van Hove point energies with respect to the Fermi level. Already for moderate tensile strain along the V plane and compressive strain normal to the V layer, we find that a van Hove point can be shifted to the Fermi energy. Such a mechanism provides an invaluable tuning knob to alter the correlation profile in the kagome metal, and suggests itself for further experimental investigation. It might allow to reconcile possible multi-dome superconductivity in kagome metals not only from phonons, but also from the viewpoint of unconventional pairing.

We report on the findings of a blind challenge devoted to determining the frozen-core, full configuration interaction (FCI) ground state energy of the benzene molecule in a standard correlation-consistent basis set of double-$\zeta$ quality. As a broad international endeavour, our suite of wave function-based correlation methods collectively represents a diverse view of the high-accuracy repertoire offered by modern electronic structure theory. In our assessment, the evaluated high-level methods are all found to qualitatively agree on a final correlation energy, with most methods yielding an estimate of the FCI value around $-863$ m$E_{\text{H}}$. However, we find the root-mean-square deviation of the energies from the studied methods to be considerable (1.3 m$E_{\text{H}}$), which in light of the acclaimed performance of each of the methods for smaller molecular systems clearly displays the challenges faced in extending reliable, near-exact correlation methods to larger systems. While the discrepancies exposed by our study thus emphasize the fact that the current state-of-the-art approaches leave room for improvement, we still expect the present assessment to provide a valuable community resource for benchmark and calibration purposes going forward.

The cubic perovskite SrFeO$_3$ was recently reported to host hedgehog- and skyrmion-lattice phases in a highly symmetric crystal structure which does not support the Dzyaloshinskii-Moriya interactions commonly invoked to explain such magnetic order. Hints of a complex magnetic phase diagram have also recently been found in powder samples of the single-layer Ruddlesden-Popper analog Sr$_2$FeO$_4$, so a reinvestigation of the bilayer material Sr$_3$Fe$_2$O$_7$, believed to be a simple helimagnet, is called for. Our magnetization and dilatometry studies reveal a rich magnetic phase diagram with at least 6 distinct magnetically ordered phases and strong similarities to that of SrFeO$_3$. In particular, at least one phase is apparently multiple-$\mathbf{q}$, and the $\mathbf{q}$s are not observed to vary among the phases. Since Sr$_3$Fe$_2$O$_7$ has only two possible orientations for its propagation vector, some of the phases are likely exotic multiple-$\mathbf{q}$ order, and it is possible to fully detwin all phases and more readily access their exotic physics.

We consider the low-energy excitations of one-dimensional spin-orbital models which consist of spin waves, orbital waves, and joint spin-orbital excitations. Among the latter we identify strongly entangled spin-orbital bound states which appear as peaks in the von Neumann entropy (vNE) spectral function introduced in this work. The strong entanglement of bound states is manifested by a universal logarithmic scaling of the vNE with system size, while the vNE of other spin-orbital excitations saturates. We suggest that spin-orbital entanglement can be experimentally explored by the measurement of the dynamical spin-orbital correlations using resonant inelastic x-ray scattering, where strong spin-orbit coupling associated with the core hole plays a role.

Reduced dimensionality and strong electronic correlations, which are among the most important ingredients for cupratelike high-Tc superconductivity, characterize also the physics of nickelate-based heterostructures. Starting from the local-density approximation we arrive at a simple two-band model for quasi-two-dimensional 2D LaNiO3 /LaAlO3 heterostructures and extend it by introducing an appropriate hopping in the z direction to describe the dimensional crossover to three dimensions 3D. Using dynamical mean-field theory, we study the effects of electronic correlations with increasing interaction strength along the crossover from 2D to 3D. Qualitatively, the effects of electronic correlations are surprisingly similar, albeit quantitatively larger interaction strengths are required in three dimensions for getting a Mott-Hubbard insulating state. The exchange parameters of an effective Kugel-Khomskii-type spin-orbital model are also derived and reveal strong antiferromagnetic tendencies.

The ability to control the properties of twisted bilayer transition metal dichalcogenides in situ makes them an ideal platform for investigating the interplay of strong correlations and geometric frustration. Of particular interest are the low energy scales, which make it possible to experimentally access both temperature and magnetic fields that are of the order of the bandwidth or the correlation scale. In this manuscript we analyze the moiré Hubbard model, believed to describe the low energy physics of an important subclass of the twisted bilayer compounds. We establish its magnetic and the metal-insulator phase diagram for the full range of magnetic fields up to the fully spin polarized state. We find a rich phase diagram including fully and partially polarized insulating and metallic phases of which we determine the interplay of magnetic order, Zeeman-field, and metallicity, and make connection to recent experiments.

A Kondo model with symplectic symmetry was recently put forward as the effective low-energy theory of a superconducting-island device coupled to multiple leads. This model, which possesses non-Fermi liquid physics and effective anyons, was argued to belong to the class of topological Kondo effects. Here, we clarify the extent of stability of its exotic fixed point using perturbative and numerical renormalization group in conjunction with bosonization and conformal field theory. In contrast to previous claims, we show that asymmetry in the coupling to the leads destabilizes the non-Fermi liquid. Other destabilizing perturbations include asymmetry in the superconducting pairing or internal energy of the individual quantum dots in the island. Nevertheless, these perturbations all generate the same relevant operators. Thus, only a small number of couplings need to be tuned individually, and these can be selected according to experimental convenience. Our results highlight a common misconception that anisotropy in single-channel Kondo couplings is always irrelevant. As demonstrated, relevant terms will emerge whenever the group generators do not span the full space of impurity operators. This calls for a more detailed inspection of models that exhibit this property, such as large-spin impurities and SO(M) Kondo models.

Nodal noncentrosymmetric superconductors have topologically nontrivial properties manifested by protected zero-energy surface states. Specifically, it was recently found that zero-energy surface flat bands of topological origin appear at their surface. We show that the presence of certain inversion-type lattice symmetries can give rise to additional topological features of the gap nodes, resulting in surface states forming one-dimensional arcs connecting the projections of two nodal rings. In addition, we demonstrate that Majorana surface states can appear at time-reversal-invariant momenta of the surface Brillouin zone, even when the system is not fully gapped in the bulk. Within a continuum theory we derive the topological invariants that protect these different types of zero-energy surface states. We independently derive general conditions for the existence of zero-energy surface bound states using the complementary quasiclassical scattering theory, explicitly taking into account the effects of spin-orbit splitting of the bands. We compute surface bound-state spectra for various crystal point-group symmetries and orbital-angular-momentum pairing states. Finally, we examine the signatures of the arc surface states and of the zero-energy surface flat bands in tunneling-conductance spectra and discuss how topological phase transitions in noncentrosymmetric superconductors could be observed in experiments.

Topological superconductors have become a subject of intense research due to their potential use for technical applications in device fabrication and quantum information. Besides fully gapped superconductors, unconventional superconductors with point or line nodes in their order parameter can also exhibit nontrivial topological characteristics. This article reviews recent progress in the theoretical understanding of nodal topological superconductors, with a focus on Weyl and noncentrosymmetric superconductors and their protected surface states. Using selected examples, we review the bulk topological properties of these systems, study different types of topological surface states, and examine their unusual properties. Furthermore, we survey some candidate materials for topological superconductivity and discuss different experimental signatures of topological surface states.

We generalize the concept of separable dual-space Gaussian pseudopotentials to the relativistic case. This allows us to construct this type of pseudopotential for the whole periodic table and we present a complete table of pseudopotential parameters for all the elements from H to Rn. The relativistic version of this pseudopotential retains all the advantages of its nonrelativistic version. It is separable by construction, it is optimal for integration on a real space grid, it is highly accurate and due to its analytic form it can be specified by a very small number of parameters. The accuracy of the pseudopotential is illustrated by an extensive series of molecular calculations.

We study the spectral function of a single hole doped into the (a,b) plane of the Mott insulator LaVO$_3$, with antiferromagnetic (AF) spin order of S=1 spins accompanied by alternating orbital (AO) order of active $\{d_{yz},d_{zx}\}$ orbitals. Starting from the respective t-J model, with spin-orbital superexchange and effective three-site hopping terms, we derive the polaron Hamiltonian and show that a hole couples simultaneously to the collective excitations of the AF/AO phase, magnons and orbitons. Next, we solve this polaron problem using the self-consistent Born approximation and find a stable quasiparticle solution -- a spin-orbital polaron. We show that the spin-orbital polaron resembles the orbital polaron found in $e_g$ systems, as e.g. in K$_2$CuF$_4$ or (to some extent) in LaMnO$_3$, and that the hole may be seen as confined in a string-like potential. However, the spins also play a crucial role in the formation of this polaron -- we explain how the orbital degrees of freedom: (i) confine the spin dynamics acting on the hole as the classical Ising spins, and (ii) generate the string potential which is of the joint spin-orbital character. Finally, we discuss the impact of the results presented here on the understanding of the phase diagrams of the lightly doped cubic vanadates.

Laboratory-scale precision experiments are a promising approach to searching for physics beyond the standard model. Non-centrosymmetric solids offer favorable statistical sensitivity for efforts that search for new fields, whose interactions violate the discrete parity and time-reversal symmetries. One example is the electric Cosmic Axion Spin Precession Experiment (CASPEr-e), which is sensitive to the defining interaction of the QCD axion dark matter with gluons in atomic nuclei. The effective electric field is the parameter that quantifies the sensitivity of such experiments to new physics. We describe the theoretical approach to calculating the effective electric field for non-centrosymmetric sites in ionic insulating solids. We consider the specific example of the EuCl$_3\cdot$6H$_2$O crystal, which is a particularly promising material. The optimistic estimate of the effective electric field for the $^{153}$Eu isotope in this crystal is 10 MV/cm. The calculation uncertainty is estimated to be two orders of magnitude, dominated by the evaluation of the Europium nuclear Schiff moment.

In the normal metal/ferromagnetic insulator bilayer (such as Pt/Y$_{3}$Fe$_{5}$O$_{12}$) and the normal metal/ferromagnetic metal/oxide trilayer (such as Pt/Co/AlO$_{x}$) where spin injection and ejection are achieved by the spin Hall effect in the normal metal, we propose a minimal model based on quantum tunneling of spins to explain the spin-transfer torque and spin pumping caused by the spin Hall effect. The ratio of their damping-like to field-like component depends on the tunneling wave function that is strongly influenced by generic material properties such as interface $s-d$ coupling, insulating gap, and layer thickness, yet the spin relaxation plays a minor role. The quantified result renders our minimal model an inexpensive tool for searching for appropriate materials.

Collective excitation modes are a characteristic feature of symmetry-broken phases of matter. For example, superconductors exhibit an amplitude Higgs mode and a phase mode, which are the radial and angular excitations in the Mexican-hat potential of the free energy. In two-band superconductors there exists in addition a Leggett phase mode, which corresponds to collective fluctuations of the interband phase difference. In equilibrium systems amplitude and phase modes are decoupled, since they are mutually orthogonal excitations. The direct detection of Higgs and Leggett modes by linear-response measurements is challenging, because they are often overdamped and do not couple directly to the electromagnetic field. In this work, using numerical exact simulations we show for the case of two-gap superconductors, that optical pump-probe experiments excite both Higgs and Leggett modes out of equilibrium. We find that this non-adiabatic excitation process introduces a strong interaction between the collective modes. Moreover, we predict that the coupled Higgs and Leggett modes are clearly visible in the pump-probe absorption spectra as oscillations at their respective frequencies.

Three-particle complexes consisting of two holes in the completely filled zero electron Landau level and an excited electron in the unoccupied first Landau level are investigated in a quantum Hall insulator. The distinctive features of these three-particle complexes are an electron-hole mass symmetry and the small energy gap of the quantum Hall insulator itself. Theoretical calculations of the trion energy spectrum in a quantizing magnetic field predict that, besides the ground state, trions feature a hierarchy of excited bound states. In agreement with the theoretical simulations, we observe new photoluminescence lines related to the excited trion states. A relatively small energy gap allows the binding of three-particle complexes with magnetoplasma oscillations and formation of plasmarons. The plasmaron properties are investigated experimentally.

Principles that predict reactions or properties of materials define the discipline of chemistry. In this work we derive chemical rules, based on atomic distances and chemical bond character, which predict topological materials in compounds that feature the structural motif of a square-net. Using these rules we identify over 300 potential new topological materials. We show that simple chemical heuristics can be a powerful tool to characterize topological matter. In contrast to previous database-driven materials categorization our approach allows us to identify candidates that are alloys, solid-solutions, or compounds with statistical vacancies. While previous material searches relied on density functional theory, our approach is not limited by this method and could also be used to discover magnetic and statistically-disordered topological semimetals.

A first-order-like resistivity hysteresis is induced by a subtle structural transition under hydrostatic pressure in the topological nodal-line superconductor PbTaSe$_2$. This structure transition is quickly suppressed to zero at pressure $\sim$0.25 GPa. As a result, superconductivity shows a marked suppression, accompanied with fundamental changes in the magnetoresistance and Hall resistivity, suggesting a Lifshitz transition around $\sim$0.25 GPa. The first principles calculations show that the spin-orbit interactions partially gap out the Dirac nodal line around $K$ point in the Brillouin zone upon applying a small pressure, whilst the Dirac states around $H$ point are completely destroyed. The calculations further reveal a second structural phase transition under a pressure as high as $\sim$30 GPa, through which a transition from a topologically nontrivial phase to a trivial phase is uncovered, with a superconducting dome emerging under this high-pressure phase.

We investigate the Landau parameters for the instabilities in spin and charge channels in the nondegenerate extended Hubbard model with intersite Coulomb and exchange interactions. To this aim we use the spin rotationally invariant slave boson approach and we determine the necessary inverse propagator matrix. The analytically derived spin Landau parameter $F_0^a$ for the half filled band uncovers the intrinsic instability of the nondegenerate Hubbard model towards ferromagnetism --- negative intersite exchange interaction triggers a ferromagnetic instability at half filling before the metal-insulator transition, indicated by the divergence of the magnetic susceptibility at $F_0^a=-1$. This result is general and the instability occurs in the strongly correlated metallic regime for any lattice, in three or two dimensions. Next as an illustrative example we present numerical results obtained for the cubic lattice with nearest neighbor exchange $J$ and Coulomb $V$ elements and arbitrary electron density. One finds that the range of small doping near half filling is the most unstable one towards spin polarization, but only in the case of ferromagnetic intersite exchange J<0. Charge Landau parameter $F_0^s$ is lowered near half filling by increasing $U$ when the intersite Coulomb interaction $V$ is attractive, but in contrast to $F_0^a$ at J<0 it requires an attraction beyond a critical value $V_c$ to generate the divergence of the charge susceptibility at $F_0^s=-1$ in the metallic phase. This instability was found for a broad range of electronic filling away from half filling for moderate attraction.