Low-Rank Adaptation (LoRA) enables efficient fine-tuning of pre-trained language models through low-rank matrix approximation, achieving effectiveness in many scenarios. However, its representation capacity is constrained in complex tasks or high-rank dependency settings, potentially limiting model adaptability. To overcome the expressive bottleneck in classical low-rank approximation for fine-tuning large language models (LLMs), we propose Quantum Tensor Hybrid Adaptation (QTHA), a parameter-efficient fine-tuning method that integrates a quantum neural network (QNN) with a tensor network. QTHA explores quantum tensor hybrid fine-tuning within low-rank spaces by decomposing pre-trained weights into quantum neural network and tensor network representations, leveraging quantum state superposition to overcome classical rank limitations. Experiments demonstrate that QTHA achieves performance comparable to or surpassing LoRA in parameter-efficient fine-tuning. Compared to LoRA, QTHA reduces trainable parameters by 76% while reducing training loss by up to 17% and improving test set performance by up to 17% within the same training steps. This research not only enables lightweight adaptation of quantum resources to the billion-parameter models but also validates the feasibility of quantum hardware optimization driven by LLM tasks. It establishes the first engineering-ready foundation for future quantum-enhanced Artificial General Intelligence (AGI) systems.

To realize large-scale quantum information processes, an ideal scheme for two-qubit operations should enable diverse operations with given hardware and physical interaction. However, for spin qubits in semiconductor quantum dots, the common two-qubit operations, including CPhase gates, SWAP gates, and CROT gates, are realized with distinct parameter regions and control waveforms, posing challenges for their simultaneous implementation. Here, taking advantage of the inherent Heisenberg interaction between spin qubits, we propose and verify a fast composite two-qubit gate scheme to extend the available two-qubit gate types as well as reduce the requirements for device properties. Apart from the formerly proposed CPhase (controlled-phase) gates and SWAP gates, theoretical results indicate that the iSWAP-family gate and Fermionic simulation (fSim) gate set are additionally available for spin qubits. Meanwhile, our gate scheme limits the parameter requirements of all essential two-qubit gates to a common J~{\Delta}E_Z region, facilitate the simultaneous realization of them. Furthermore, we present the preliminary experimental demonstration of the composite gate scheme, observing excellent match between the measured and simulated results. With this versatile composite gate scheme, broad-spectrum two-qubit operations allow us to efficiently utilize the hardware and the underlying physics resources, helping accelerate and broaden the scope of the upcoming noise intermediate-scale quantum (NISQ) computing.

Achieving a practical quantum speedup for deep neural networks (DNNs) remains a central yet elusive goal, hindered by the dual challenges of constructing deep architectures and the prohibitive overhead of data loading and measurement. We introduce a framework to overcome these barriers, specifically targeting an asymptotic speedup with respect to the large input dimensions of modern DNNs (e.g., sequence length or image size). Our framework enables the design of multi-layer Quantum ResNet and Quantum Transformer models by strategically decomposing tasks: computationally intensive operations on the large input dimension are assigned to quantum linear algebra subroutines, while operations on the smaller, fixed feature dimension are handled by efficient quantum arithmetic. A cornerstone of our approach is a novel data transfer protocol, Discrete Chebyshev Decomposition (DCD), which facilitates this modularity. Numerical validation reveals a pivotal insight: the measurement cost required to maintain a target accuracy scales sublinearly with the input dimension. This sublinear scaling is the key to preserving the quantum advantage, ensuring that I/O overhead does not nullify the computational gains. A rigorous resource analysis further corroborates the superiority of our models in both efficiency and flexibility. Powered by this targeted acceleration strategy and the efficiency of DCD, our framework establishes a viable path toward scalable quantum deep learning.

In emerging quantum-classical integration applications, the classical time cost-especially from compilation and protocol-level communication often exceeds the execution time of quantum circuits themselves, posing a severe bottleneck to practical deployment. To overcome these limitations, QPanda3 has been extensively optimized as a high-performance quantum programming framework tailored for the demands of the NISQ era and quantum-classical hybrid workflows. It features optimized circuit compilation, a custom binary instruction stream (OriginBIS), and hardware-aware execution strategies to significantly reduce latency and communication overhead. OriginBIS achieves up to 86.9$\times$ faster encoding and 35.6$\times$ faster decoding than OpenQASM 2.0, addressing critical bottlenecks in hybrid quantum systems. Benchmarks show 10.7$\times$ compilation speedup and up to 597$\times$ acceleration in compiling large-scale circuits (e.g., a 118-qubit W-state) compared to Qiskit. n high-performance simulation, QPanda3 excels in variational quantum algorithms, achieving up to 26$\times$ faster gradient computation than Qiskit, with minimal time-complexity growth across circuit depths. These capabilities make QPanda3 well-suited for scalable quantum algorithm development in finance, materials science, and combinatorial optimization, while supporting industrial deployment and cloud-based execution in quantum-classical hybrid computing scenarios.

Cryogenic characterization and modeling of 0.18um CMOS technology (1.8V and 5V) are presented in this paper. Several PMOS and NMOS transistors with different width to length ratios(W/L) were extensively characterized under various bias conditions at temperatures ranging from 300K down to 4.2K. We extracted their fundamental physical parameters and developed a compact model based on BSIM3V3. In addition to their I-V characteristics, threshold voltage(Vth) values, on/off current ratio, transconductance of the MOS transistors, and resistors on chips are measured at temperatures from 300K down to 4.2K. A simple subcircuit was built to correct the kink effect. This work provides experimental evidence for implementation of cryogenic CMOS technology, a valid industrial tape-out process model, and romotes the application of integrated circuits in cryogenic environments, including quantum measurement and control systems for quantum chips at very low temperatures.

With the birth of Noisy Intermediate Scale Quantum (NISQ) devices and the verification of "quantum supremacy" in random number sampling and boson sampling, more and more fields hope to use quantum computers to solve specific problems, such as aerodynamic design, route allocation, financial option prediction, quantum chemical simulation to find new materials, and the challenge of quantum cryptography to automotive industry security. However, these fields still need to constantly explore quantum algorithms that adapt to the current NISQ machine, so a quantum programming framework that can face multi-scenarios and application needs is required. Therefore, this paper proposes QPanda, an application scenario-oriented quantum programming framework with high-performance simulation. Such as designing quantum chemical simulation algorithms based on it to explore new materials, building a quantum machine learning framework to serve finance, etc. This framework implements high-performance simulation of quantum circuits, a configuration of the fusion processing backend of quantum computers and supercomputers, and compilation and optimization methods of quantum programs for NISQ machines. Finally, the experiment shows that quantum jobs can be executed with high fidelity on the quantum processor using quantum circuit compile and optimized interface and have better simulation performance.

Material disorders are one of the major sources of noise and loss in solid-state quantum devices, whose behaviors are often modeled as two-level systems (TLSs) formed by charge tunneling between neighboring sites. However, the role of their spins in tunneling and its impact on device performance remain highly unexplored. In this work, employing ultra-thin TiN superconducting resonators, we reveal anomalous TLS behaviors by demonstrating an unexpected increase in resonant frequency at low magnetic fields. Furthermore, a spin-flip TLS model is proposed, in which an effective spin-orbit coupling is generated by inhomogeneous local magnetic fields from defect spins. This mechanism mixes charge tunnelings and spin flips, quantitatively reproducing the observed frequency-field relationship and its temperature dependence. This work deepens the understanding of spin-dependent TLS behaviors, offering the possibility of magnetically engineering noise and loss in solid-state quantum devices.

Solving combinatorial optimization problems using variational quantum algorithms (VQAs) might be a promise application in the NISQ era. However, the limited trainability of VQAs could hinder their scalability to large problem sizes. In this paper, we improve the trainability of variational quantum eigensolver (VQE) by utilizing convex interpolation to solve portfolio optimization. Based on convex interpolation, the location of the ground state can be evaluated by learning the property of a small subset of basis states in the Hilbert space. This enlightens naturally the proposals of the strategies of close-to-solution initialization, regular cost function landscape, and recursive ansatz equilibrium partition. The successfully implementation of a $40$-qubit experiment using only $10$ superconducting qubits demonstrates the effectiveness of our proposals. Furthermore, the quantum inspiration has also spurred the development of a prototype greedy algorithm. Extensive numerical simulations indicate that the hybridization of VQE and greedy algorithms achieves a mutual complementarity, combining the advantages of both global and local optimization methods. Our proposals can be extended to improve the trainability for solving other large-scale combinatorial optimization problems that are widely used in real applications, paving the way to unleash quantum advantages of NISQ computers in the near future.

Operation speed and coherence time are two core measures for the viability of a qubit. Strong spin-orbit interaction (SOI) and relatively weak hyperfine interaction make holes in germanium (Ge) intriguing candidates for spin qubits with rapid, all-electrical coherent control. Here we report ultrafast single-spin manipulation in a hole-based double quantum dot in a germanium hut wire (GHW). Mediated by the strong SOI, a Rabi frequency exceeding 540 MHz is observed at a magnetic field of 100 mT, setting a record for ultrafast spin qubit control in semiconductor systems. We demonstrate that the strong SOI of heavy holes (HHs) in our GHW, characterized by a very short spin-orbit length of 1.5 nm, enables the rapid gate operations we accomplish. Our results demonstrate the potential of ultrafast coherent control of hole spin qubits to meet the requirement of DiVincenzo's criteria for a scalable quantum information processor.

Pulse distortion, as one of the coherent error sources, hinders the characterization and control of qubits. In the semiconductor quantum dot system, the distortions on measurement pulses and control pulses disturb the experimental results, while no effective calibration procedure has yet been reported. Here, we demonstrate two different calibration methods to calibrate and correct the distortion using the two-qubit system as a detector. The two calibration methods have different correction accuracy and complexity. One is the coarse predistortion (CPD) method, with which the distortion is partly relieved. The other method is the all predistortion (APD) method, with which we measure the transfer function and significantly improve the exchange oscillation homogeneity. The two methods use the exchange oscillation homogeneity as the metric and are appropriate for any qubit that oscillates with a diabatic pulse. With the APD procedure, an arbitrary control waveform can be accurately delivered to the device, which is essential for characterizing qubits and improving gate fidelity.

Strong spin-orbit coupling and relatively weak hyperfine interactions make germanium hole spin qubits a promising candidate for semiconductor quantum processors. The two-dimensional hole gas structure of strained Ge quantum wells serves as the primary material platform for spin hole qubits.A low disorder material environment is essential for this process. In this work, we fabricated a Ge/SiGe heterojunction with a 60 nm buried quantum well layer on a Si substrate using reduced pressure chemical vapor deposition technology. At a temperature of 16 mK, when the carrier density is 1.87*10^11/cm2, we obtained a mobility as high as 308.64*10^4cm2/Vs. Concurrently, double quantum dot and planar germanium coupling with microwave cavities were also successfully achieved.This fully demonstrates that this structure can be used for the preparation of higher-performance hole spin qubits.

With the rapid development of classical and quantum machine learning, a large number of machine learning frameworks have been proposed. However, existing machine learning frameworks usually only focus on classical or quantum, rather than both. Therefore, based on VQNet 1.0, we further propose VQNet 2.0, a new generation of unified classical and quantum machine learning framework that supports hybrid optimization. The core library of the framework is implemented in C++, and the user level is implemented in Python, and it supports deployment on quantum and classical hardware. In this article, we analyze the development trend of the new generation machine learning framework and introduce the design principles of VQNet 2.0 in detail: unity, practicality, efficiency, and compatibility, as well as full particulars of implementation. We illustrate the functions of VQNet 2.0 through several basic applications, including classical convolutional neural networks, quantum autoencoders, hybrid classical-quantum networks, etc. After that, through extensive experiments, we demonstrate that the operation speed of VQNet 2.0 is higher than the comparison method. Finally, through extensive experiments, we demonstrate that VQNet 2.0 can deploy on different hardware platforms, the overall calculation speed is faster than the comparison method. It also can be mixed and optimized with quantum circuits composed of multiple quantum computing libraries.

Quantum Random Access Memory (QRAM) is a critical component for loading classical data into quantum computers. While constructing a practical QRAM presents several challenges, including the impracticality of an infinitely large QRAM size and a fully error-correction implementation, it is essential to consider a practical case where the QRAM has a limited size. In this work, we focus on the access of larger data sizes without keeping on increasing the size of the QRAM. Firstly, we address the challenge of word length, as real-world datasets typically have larger word lengths than the single-bit data that most previous studies have focused on. We propose a novel protocol for loading data with larger word lengths $k$ without increasing the number of QRAM levels $n$. By exploiting the parallelism in the data query process, our protocol achieves a time complexity of $O(n+k)$ and improves error scaling performance compared to existing approaches. Secondly, we provide a data-loading method for general-sized data access tasks when the number of data items exceeds $2^n$, which outperforms the existing hybrid QRAM+QROM architecture. Our method contributes to the development of time and error-optimized data access protocols for QRAM devices, reducing the qubit count and error requirements for QRAM implementation, and making it easier to construct practical QRAM devices with a limited number of physical qubits.

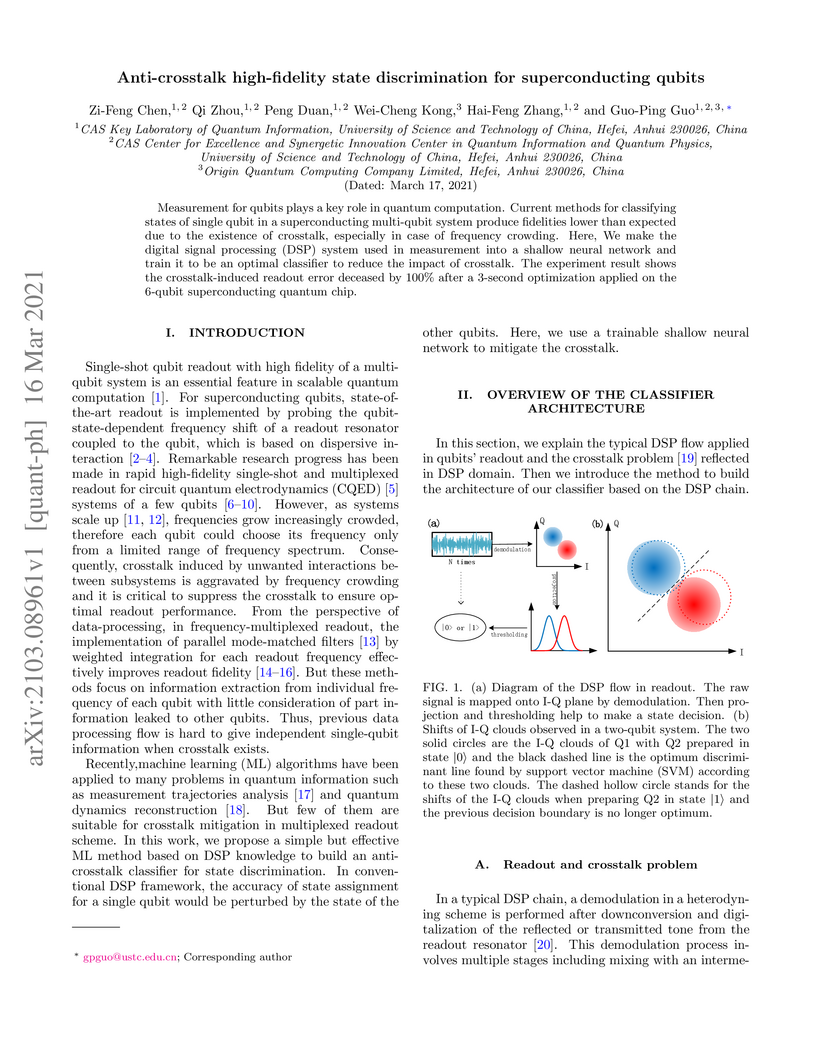
Measurement for qubits plays a key role in quantum computation. Current methods for classifying states of single qubit in a superconducting multi-qubit system produce fidelities lower than expected due to the existence of crosstalk, especially in case of frequency crowding. Here, We make the digital signal processing (DSP) system used in measurement into a shallow neural network and train it to be an optimal classifier to reduce the impact of crosstalk. The experiment result shows the crosstalk-induced readout error deceased by 100% after a 3-second optimization applied on the 6-qubit superconducting quantum chip.

Preserving qubit coherence and maintaining high-fidelity qubit control under complex noise environment is an enduring challenge for scalable quantum computing. Here we demonstrate an addressable fault-tolerant single spin qubit with an average control fidelity of 99.12% via randomized benchmarking on a silicon quantum dot device with an integrated micromagnet. Its dephasing time T2* is 1.025 us and can be enlarged to 264 us by using the Hahn echo technique, reflecting strong low-frequency noise in our system. To break through the noise limitation, we introduce geometric quantum computing to obtain high control fidelity by exploiting its noise-resilient feature. However, the control fidelities of the geometric quantum gates are lower than 99%. According to our simulation, the noise-resilient feature of geometric quantum gates is masked by the heating effect. With further optimization to alleviate the heating effect, geometric quantum computing can be a potential approach to reproducibly achieving high-fidelity qubit control in a complex noise environment.

It is the first step for understanding how RNA structure folds from base sequences that to know how its secondary structure is formed. Traditional energy-based algorithms are short of precision, particularly for non-nested sequences, while learning-based algorithms face challenges in obtaining high-quality training data. Recently, quantum annealer has rapidly predicted the folding of the secondary structure, highlighting that quantum computing is a promising solution to this problem. However, gate model algorithms for universal quantum computing are not available. In this paper, gate-based quantum algorithms will be presented, which are highly flexible and can be applied to various physical devices. Mapped all possible secondary structure to the state of a quadratic Hamiltonian, the whole folding process is described as a quadratic unconstrained binary optimization model. Then the model can be solved through quantum approximation optimization algorithm. We demonstrate the performance with both numerical simulation and experimental realization. Throughout our benchmark dataset, simulation results suggest that our quantum approach is comparable in accuracy to classical methods. For non-nested sequences, our quantum approach outperforms classical energy-based methods. Experimental results also indicate our method is robust in current noisy devices. It is the first instance of universal quantum algorithms being employed to tackle RNA folding problems, and our work provides a valuable model for utilizing universal quantum computers in solving RNA folding problems.

In silicon quantum dots (QDs), at a certain magnetic field commonly referred to as the "hot spot", the electron spin relaxation rate (T_1^(-1)) can be drastically enhanced due to strong spin-valley mixing. Here, we experimentally find that with a valley splitting of 78.2 ${\pm}$ 1.6 ${\mu}$eV, this hot spot in spin relaxation can be suppressed by more than 2 orders of magnitude when the in-plane magnetic field is oriented at an optimal angle, about 9{\deg} from the [100] sample plane. This directional anisotropy exhibits a sinusoidal modulation with a 180{\deg} periodicity. We explain the magnitude and phase of this modulation using a model that accounts for both spin-valley mixing and intravalley spin-orbit mixing. The generality of this phenomenon is also confirmed by tuning the electric field and the valley splitting up to 268.2 ${\pm}$ 0.7 ${\mu}$eV.

We demonstrate a switchable electron shell structure in a bilayer graphene quantum dot by manipulating the trigonal warping effect upon electrical gating. Under a small perpendicular electric field, the lowest s-shell is sequentially filled with two spin-up and two spin-down electrons of opposite valleys. When increasing the electric field, an additional three-fold minivalley degeneracy is generated so that the s-shell can be filled with 12 electrons with the first/last 6 electrons having the same spin polarization. The switched spin filling sequence demonstrates the possibility of using the trigonal warping effect to electrically access and manipulate the spin degree of freedom in bilayer graphene.

The excellent mechanical properties make graphene promising for realizing nanomechanical resonators with high resonant frequencies, large quality factors, strong nonlinearities, and the capability to effectively interface with various physical systems. Equipped with gate electrodes, it has been demonstrated that these exceptional device properties can be electrically manipulated, leading to a variety of nanomechanical/acoustic applications. Here, we review the recent progress of graphene nanomechanical resonators with a focus on their electrical tunability. First, we provide an overview of different graphene nanomechanical resonators, including their device structures, fabrication methods, and measurement setups. Then, the key mechanical properties of these devices, for example, resonant frequencies, nonlinearities, dissipations, and mode coupling mechanisms, are discussed, with their behaviors upon electrical gating being highlighted. After that, various potential classical/quantum applications based on these graphene nanomechanical resonators are reviewed. Finally, we briefly discuss challenges and opportunities in this field to offer future prospects of the ongoing studies on graphene nanomechanical resonators.