computational-complexity
We study the problem of certifying local Hamiltonians from real-time access to their dynamics. Given oracle access to e−itH for an unknown k-local Hamiltonian H and a fully specified target Hamiltonian H0, the goal is to decide whether H is exactly equal to H0 or differs from H0 by at least ε in normalized Frobenius norm, while minimizing the total evolution time. We introduce the first intolerant Hamiltonian certification protocol that achieves optimal performance for all constant-locality Hamiltonians. For general n-qubit, k-local, traceless Hamiltonians, our procedure uses O(ck/ε) total evolution time for a universal constant c, and succeeds with high probability. In particular, for O(1)-local Hamiltonians, the total evolution time becomes Θ(1/ε), matching the known Ω(1/ε) lower bounds and achieving the gold-standard Heisenberg-limit scaling. Prior certification methods either relied on implementing inverse evolution of H, required controlled access to e−itH, or achieved near-optimal guarantees only in restricted settings such as the Ising case (k=2). In contrast, our algorithm requires neither inverse evolution nor controlled operations: it uses only forward real-time dynamics and achieves optimal intolerant certification for all constant-locality Hamiltonians.
When should an autonomous agent commit resources to a task? We introduce the Agent Capability Problem (ACP), a framework for predicting whether an agent can solve a problem under resource constraints. Rather than relying on empirical heuristics, ACP frames problem-solving as information acquisition: an agent requires \Itotal bits to identify a solution and gains \Istep bits per action at cost \Cstep, yielding an effective cost \Ceff=(\Itotal/\Istep),\Cstep that predicts resource requirements before search. We prove that \Ceff lower-bounds expected cost and provide tight probabilistic upper bounds. Experimental validation shows that ACP predictions closely track actual agent performance, consistently bounding search effort while improving efficiency over greedy and random strategies. The framework generalizes across LLM-based and agentic workflows, linking principles from active learning, Bayesian optimization, and reinforcement learning through a unified information-theoretic lens. \
A language is said to be in catalytic logspace if we can test membership using a deterministic logspace machine that has an additional read/write tape filled with arbitrary data whose contents have to be restored to their original value at the end of the computation. The model of catalytic computation was introduced by Buhrman et al [STOC2014].
As our first result, we obtain a catalytic logspace algorithm for computing a minimum weight witness to a search problem, with small weights, provided the algorithm is given oracle access for the corresponding weighted decision problem. In particular, our reduction yields CL algorithms for the search versions of the following three problems: planar perfect matching, planar exact perfect matching and weighted arborescences in weighted digraphs.
Our second set of results concern the significantly larger class CL^{NP}_{2-round}. We show that CL^{NP}_{2-round} contains SearchSAT and the complexity classes BPP, MA and ZPP^{NP[1]}. While SearchSAT is shown to be in CL^{NP}_{2-round} using the isolation lemma, the other three containments, while based on the compress-or-random technique, use the Nisan-Wigderson [JCSS 1994] based pseudo-random generator. These containments show that CL^{NP}_{2-round} resembles ZPP^NP more than P^{NP}, providing some weak evidence that CL is more like ZPP than P.
For our third set of results we turn to isolation well inside catalytic classes. We consider the unambiguous catalytic class CUTISP[poly(n),logn,log^2n] and show that it contains reachability and therefore NL. This is a catalytic version of the result of van Melkebeek & Prakriya [SIAM J. Comput. 2019]. Building on their result, we also show a tradeoff between workspace and catalytic space. Finally, we extend these catalytic upper bounds to LogCFL.
The \emph{sum-of-squares (SoS) complexity} of a d-multiquadratic polynomial f (quadratic in each of d blocks of n variables) is the minimum s such that f=∑i=1sgi2 with each gi d-multilinear. In the case d=2, Hrubeš, Wigderson and Yehudayoff (2011) showed that an n1+Ω(1) lower bound on the SoS complexity of explicit biquadratic polynomials implies an exponential lower bound for non-commutative arithmetic circuits. In this paper, we establish an analogous connection between general \emph{multiquadratic sum-of-squares} and \emph{commutative arithmetic formulas}. Specifically, we show that an nd−o(logd) lower bound on the SoS complexity of explicit d-multiquadratic polynomials, for any d=d(n) with ω(1)≤d(n)≤O(loglognlogn), would separate the algebraic complexity classes VNC1 and VNP.
Researchers at the University of Oxford present a complete classification of long-refinement graphs where the maximum vertex degree is at most 4, thereby resolving previous gaps for specific graph sizes. The work also definitively proves the non-existence of "long-refinement pairs" for any graph order n ≥ 3, which were previously an open problem.
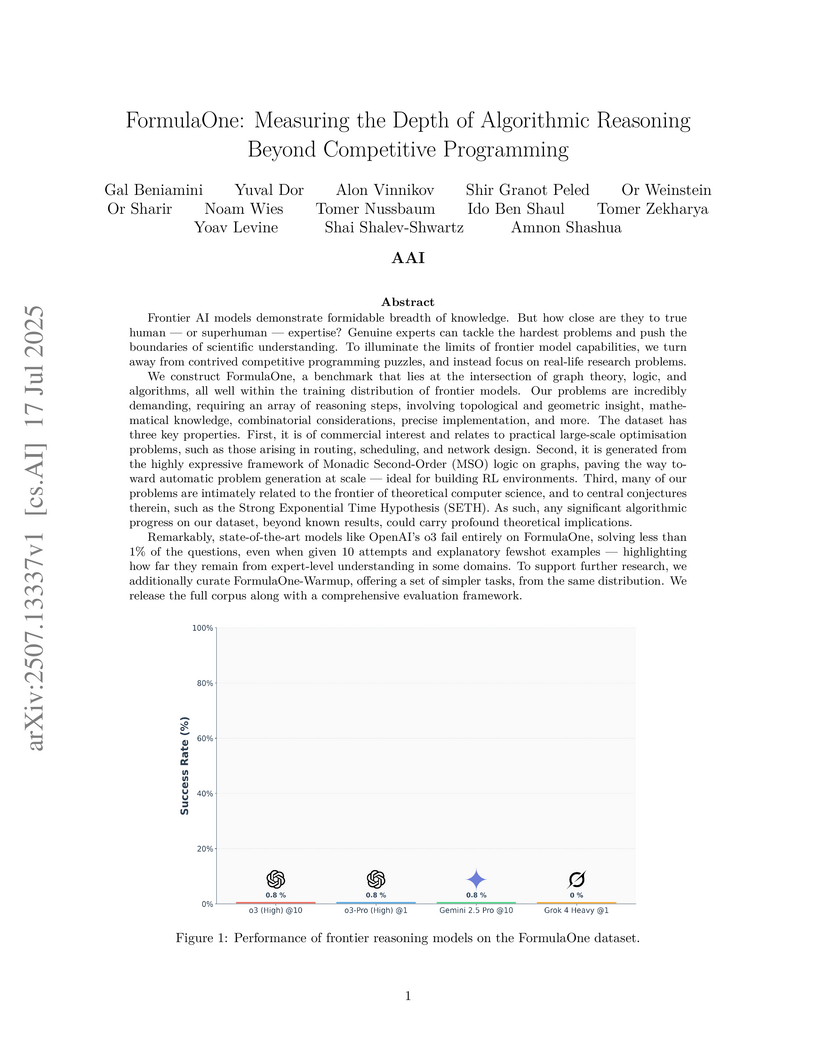
FormulaOne introduces a new benchmark for deep algorithmic reasoning, revealing that leading frontier AI models achieve less than 1% success on its challenging problems despite extensive support, which starkly contrasts with their performance on competitive programming platforms. This work suggests current models lack expert-level understanding for complex, multi-step algorithmic tasks.
This paper provides a comprehensive complexity-theoretic analysis of counting linear regions in ReLU neural networks, formalizing six distinct definitions of these regions and demonstrating that most counting problems are computationally intractable. For shallow networks, counting is #P-complete, while for deep networks, even approximating the count is NP-hard, revealing fundamental limits on analyzing network expressiveness.
Moment polytopes of tensors, the study of which is deeply rooted in invariant
theory, representation theory and symplectic geometry, have found relevance in
numerous places, from quantum information (entanglement polytopes) and
algebraic complexity theory (GCT program and the complexity of matrix
multiplication) to optimization (scaling algorithms). Towards an open problem
in algebraic complexity theory, we prove separations between the moment
polytopes of matrix multiplication tensors and unit tensors. As a consequence,
we find that matrix multiplication moment polytopes are not maximal, i.e. are
strictly contained in the corresponding Kronecker polytope. As another
consequence, we obtain a no-go result for a natural operational
characterization of moment polytope inclusion in terms of asymptotic
restriction. We generalize the separation and non-maximality to moment
polytopes of iterated matrix multiplication tensors. Our result implies that
tensor networks where multipartite entanglement structures beyond two-party
entanglement are allowed can go beyond projected entangled-pair states (PEPS)
in terms of expressivity.
Our proof characterizes membership of uniform points in moment polytopes of
tensors, and establishes a connection to polynomial multiplication tensors via
the minrank of matrix subspaces. As a result of independent interest, we extend
these techniques to obtain a new proof of the optimal border subrank bound for
matrix multiplication.
We prove that an ϵ-approximate fixpoint of a map
f:[0,1]d→[0,1]d can be found with
O(d2(logϵ1+log1−λ1)) queries to
f if f is λ-contracting with respect to an ℓp-metric for some
p∈[1,∞)∪{∞}. This generalizes a recent result of Chen, Li,
and Yannakakis [STOC'24] from the ℓ∞-case to all ℓp-metrics.
Previously, all query upper bounds for p∈[1,∞)∖{2} were
either exponential in d, logϵ1, or
log1−λ1.
Chen, Li, and Yannakakis also show how to ensure that all queries to f lie
on a discrete grid of limited granularity in the ℓ∞-case. We provide
such a rounding for the ℓ1-case, placing an appropriately defined version
of the ℓ1-case in FPdt.
To prove our results, we introduce the notion of ℓp-halfspaces and
generalize the classical centerpoint theorem from discrete geometry: for any $p
\in [1, \infty) \cup \{\infty\}$ and any mass distribution (or point set), we
prove that there exists a centerpoint c such that every ℓp-halfspace
defined by c and a normal vector contains at least a d+11-fraction
of the mass (or points).
DeepMind's PonderNet introduces a fully differentiable and probabilistic framework that enables neural networks to dynamically adjust their computation based on the complexity of the input. This method achieves state-of-the-art performance on bAbI question answering tasks with substantially reduced computation and demonstrates enhanced extrapolation capabilities on parity tasks compared to previous adaptive computation approaches.
Editing a graph to obtain a disjoint union of s-clubs is one of the models for correlation clustering, which seeks a partition of the vertex set of a graph so that elements of each resulting set are close enough according to some given criterion. For example, in the case of editing into s-clubs, the criterion is proximity since any pair of vertices (in an s-club) are within a distance of s from each other. In this work we consider the vertex splitting operation, which allows a vertex to belong to more than one cluster. This operation was studied as one of the parameters associated with the Cluster Editing problem. We study the complexity and parameterized complexity of the s-Club Cluster Edge Deletion with Vertex Splitting and s-Club Cluster Vertex Splitting problems. Both problems are shown to be NP-Complete and APX-hard. On the positive side, we show that both problems are Fixed-Parameter Tractable with respect to the number of allowed editing operations and that s-Club Cluster Vertex Splitting is solvable in polynomial-time on the class of forests.
We show that the shortest s-t path problem has the overlap-gap property in (i) sparse G(n,p) graphs and (ii) complete graphs with i.i.d. Exponential edge weights. Furthermore, we demonstrate that in sparse G(n,p) graphs, shortest path is solved by O(logn)-degree polynomial estimators, and a uniform approximate shortest path can be sampled in polynomial time. This constitutes the first example in which the overlap-gap property is not predictive of algorithmic intractability for a (non-algebraic) average-case optimization problem.
This research from the University of Illinois Urbana–Champaign establishes a theoretical foundation for the Large Language Model prompting paradigm, proving that prompting is Turing-complete. The work demonstrates that a single, finite-size Transformer can compute any computable function through appropriately crafted prompts, achieving efficient universality with specific Chain-of-Thought and precision complexity bounds.
We present a new improvement on the laser method for designing fast matrix multiplication algorithms. The new method further develops the recent advances by [Duan, Wu, Zhou FOCS 2023] and [Vassilevska Williams, Xu, Xu, Zhou SODA 2024]. Surprisingly the new improvement is achieved by incorporating more asymmetry in the analysis, circumventing a fundamental tool of prior work that requires two of the three dimensions to be treated identically. The method yields a new bound on the square matrix multiplication exponent \omega<2.371339, improved from the previous bound of \omega<2.371552. We also improve the bounds of the exponents for multiplying rectangular matrices of various shapes.
Consider the model of computation where we start with two halves of a 2n-qubit maximally entangled state. We get to apply a universal quantum computation on one half, measure both halves at the end, and perform classical postprocessing. This model, which we call 21BQP, was defined in STOC 2017 [ABKM17] to capture the power of permutational computations on special input states. As observed in [ABKM17], this model can be viewed as a natural generalization of the one-clean-qubit model (DQC1) where we learn the content of a high entropy input state only after the computation is completed. An interesting open question is to characterize the power of this model, which seems to sit nontrivially between DQC1 and BQP. In this paper, we show that despite its limitations, this model can carry out many well-known quantum computations that are candidates for exponential speed-up over classical computations (and possibly DQC1). In particular, 21BQP can simulate Instantaneous Quantum Polynomial Time (IQP) and solve the Deutsch-Jozsa problem, Bernstein-Vazirani problem, Simon's problem, and period finding. As a consequence, 21BQP also solves Order Finding and Factoring outside of the oracle setting. Furthermore, 21BQP can solve Forrelation and the corresponding oracle problem given by Raz and Tal [RT22] to separate BQP and PH. We also study limitations of 21BQP and show that similarly to DQC1, 21BQP cannot distinguish between unitaries which are close in trace distance, then give an oracle separating 21BQP and BQP. Due to this limitation, 21BQP cannot obtain the quadratic speedup for unstructured search given by Grover's algorithm [Gro96]. We conjecture that 21BQP cannot solve 3-Forrelation.
A unitary state t-design is an ensemble of pure quantum states whose moments match up to the t-th order those of states uniformly sampled from a d-dimensional Hilbert space. Typically, unitary state t-designs are obtained by evolving some reference pure state with unitaries from an ensemble that forms a design over the unitary group U(d), as unitary designs induce state designs. However, in this work we study whether Haar random symplectic states -- i.e., states obtained by evolving some reference state with unitaries sampled according to the Haar measure over SP(d/2) -- form unitary state t-designs. Importantly, we recall that random symplectic unitaries fail to be unitary designs for t>1, and that, while it is known that symplectic unitaries are universal, this does not imply that their Haar measure leads to a state design. Notably, our main result states that Haar random symplectic states form unitary t-designs for all t, meaning that their distribution is unconditionally indistinguishable from that of unitary Haar random states, even with tests that use infinite copies of each state. As such, our work showcases the intriguing possibility of creating state t-designs using ensembles of unitaries which do not constitute designs over U(d) themselves, such as ensembles that form t-designs over SP(d/2).
One-way functions are fundamental to classical cryptography and their
existence remains a longstanding problem in computational complexity theory.
Recently, a provable quantum one-way function has been identified, which
maintains its one-wayness even with unlimited computational resources. Here, we
extend the mathematical definition of functions to construct a generalized
one-way function by virtually measuring the qubit of provable quantum one-way
function and randomly assigning the corresponding measurement outcomes with
identical probability. Remarkably, using this generalized one-way function, we
have developed an unconditionally secure key distribution protocol based solely
on classical data processing, which can then utilized for secure encryption and
signature. Our work highlights the importance of information in characterizing
quantum systems and the physical significance of the density matrix. We
demonstrate that probability theory and randomness are effective tools for
countering adversaries with unlimited computational capabilities.
11 Apr 2024
This paper formally characterizes the expressive power of decoder-only transformers when allowed to generate intermediate tokens, or a 'chain of thought' (CoT), demonstrating that their computational capabilities can extend from TC0 to P depending on the number of intermediate steps. It provides the first exact characterization of a transformer class in terms of standard computational complexity classes.
We give an algorithm for finding an ϵ-fixed point of a contraction map f:[0,1]k↦[0,1]k under the ℓ∞-norm with query complexity O(klog(1/ϵ)).
Algorithms are presented that provably exceed the Goemans-Williamson approximation ratio for the NP-hard Max-Cut problem by incorporating imperfect prediction information, with specific improvements of Ω(ε⁴) for noisy predictions and Ω(ε) for partial predictions. The techniques also extend to dense 2-CSPs.
There are no more papers matching your filters at the moment.