logic
09 Dec 2025
It was shown by Visser that Peano Arithmetic has the property that any two bi-interpretable extensions of it (in the same language) are equivalent. Enayat proposed to refer to this property of a theory as tightness and to carry out a more systematic study of tightness and its stronger variants that he called neatness and solidity. Enayat proved that not only PA, but also ZF and Z2 are solid. On the other hand, it was shown in later work by a number of authors that many natural proper fragments of those theories are not even tight. Enayat asked whether there is a proper solid subtheory of the theories listed above. We answer that question in the case of PA by proving that for every n, there exist both a solid theory and a tight but not neat theory strictly between IΣn and PA. Moreover, the solid subtheories of PA can be required to be unable to interpret PA. We also obtain some other separations between properties related to tightness, for example by giving an example of a sequential theory that is neat but not semantically tight in the sense of Freire and Hamkins.
09 Dec 2025
In this note we reproduce Johnson's analysis of W2-topologies on fields of characteristic 2, which was originally stated for fields of characteristic different than 2. Following his framework, we prove that the canonical topology of an unstable field of characteristic 2 and dp-rank 2 is a V-topology. Additionally, we show that any W2-topology on a field of characteristic 2 is either induced by the intersection of two valuation rings or it is induced by dense pre-diffeo-valuation data, completing the picture for all positive characteristic fields.
Orbit-finite models of computation generalise the standard models of computation, to allow computation over infinite objects that are finite up to symmetries on atoms, denoted by A. Set theory with atoms is used to reason about these objects. Recent work assumes that A is countable and that the symmetries are the automorphisms of a structure on A. We study this set theory to understand generalisations of this approach. We show that: this construction is well-defined and sufficiently expressive; and that automorphism groups are adequate.
Certain uncountable structures appear similar to countable structures, suggesting that the theory of orbit-finite constructions may apply to these uncountable structures. We prove results guaranteeing that the theory of symmetries of two structures are equal. Let: PM(A) be the universe of symmetries induced by adding atoms in bijection with A and considering the symmetric universe; A be the image of A on the atoms; and ϕPM(A) be the relativisation of ϕ to PM(A). We prove that all symmetric universes of equality atoms have theory Th(PM(⟨N⟩)). We prove that for structures A, `nicely' covered by a set of cardinality κ, there is a structure B≡A of size κ such that for all formulae ϕ(x) in one variable, \begin{equation*}
ZFC\vdash \phi(\underline{\mathcal{A}})^{PM(\mathcal{A})}\leftrightarrow\phi(\underline{\mathcal{B}})^{PM(\mathcal{B})} \end{equation*}
04 Oct 2025
The introduction of machine learning methods has led to significant advances in automation, optimization, and discoveries in various fields of science and technology. However, their widespread application faces a fundamental limitation: the transfer of models between data domains generally lacks a rigorous mathematical justification. The key problem is the lack of formal criteria to guarantee that a model trained on one type of data will retain its properties on this http URL paper proposes a solution to this problem by formalizing the concept of analogy between data sets and models using first-order logic and Hoare this http URL formulate and rigorously prove a theorem that sets out the necessary and sufficient conditions for analogy in the task of knowledge transfer between machine learning models. Practical verification of the analogy theorem on model data obtained using the Monte Carlo method, as well as on MNIST and USPS data, allows us to achieving F1 scores of 0.84 and 0.88 for convolutional neural networks and random forests, this http URL proposed approach not only allows us to justify the correctness of transfer between domains but also provides tools for comparing the applicability of models to different types of this http URL main contribution of the work is a rigorous formalization of analogy at the level of program logic, providing verifiable guarantees of the correctness of knowledge transfer, which opens new opportunities for both theoretical research and the practical use of machine learning models in previously inaccessible areas.
17 Jul 2025
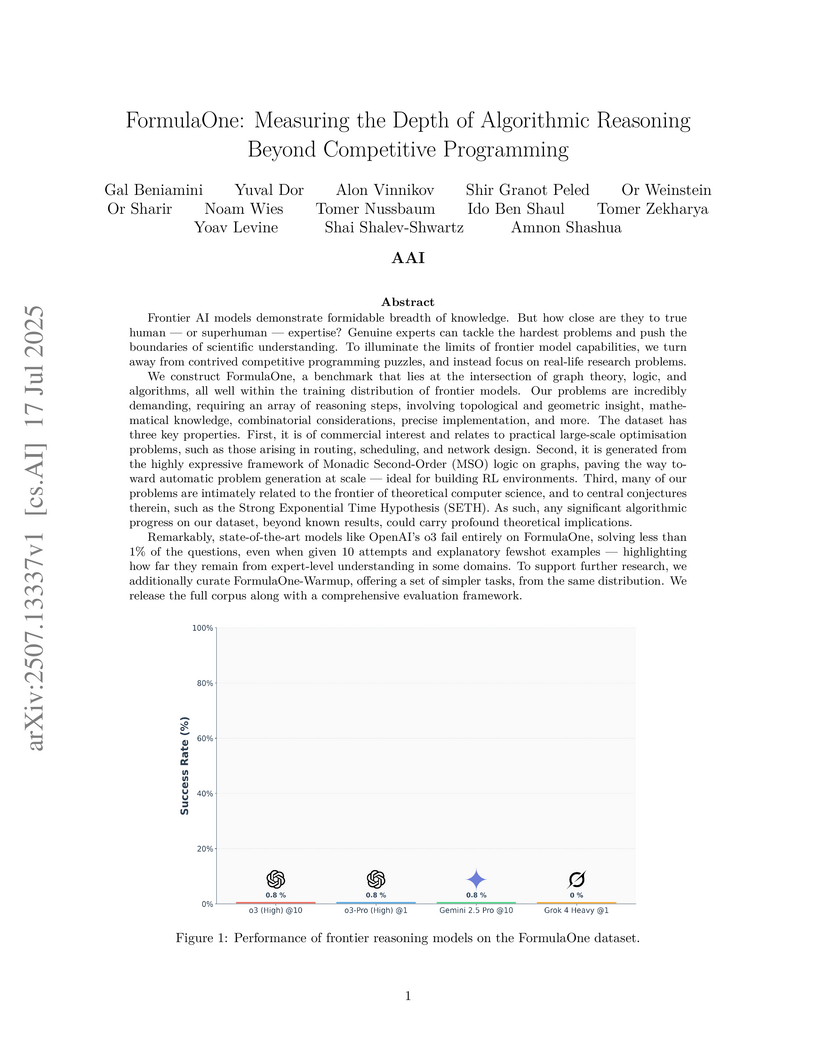
FormulaOne introduces a new benchmark for deep algorithmic reasoning, revealing that leading frontier AI models achieve less than 1% success on its challenging problems despite extensive support, which starkly contrasts with their performance on competitive programming platforms. This work suggests current models lack expert-level understanding for complex, multi-step algorithmic tasks.
25 Apr 2025
We prove that for any two regular cardinals \omega<\lambda_0<\lambda_1
there is a ccc forcing extension where there is an ultrafilter U on ω
with a base B such that $(\mathcal{B},\supseteq^*)\cong
\lambda_0\times\lambda_1$. We use similar ideas to construct an ultrafilter
with a base B as above which is order isomorphic to any given
two-dimensional, well-founded, countably directed order with no maximal
element. Similarly, relative to a supercompact cardinal, it is consistent that
κ is supercompact, and for any regular cardinals
\kappa<\lambda_0<\lambda_1<...<\lambda_n, there is a {<}\kappa-directed
closed κ+-cc forcing extension where there is a normal ultrafilter U
on κ with a base B such that $(\mathcal{B},\supseteq^*)\cong
\lambda_0\times...\times\lambda_n$. We apply our constructions to obtain
ultrafilters with controlled Tukey-type, in particular, an ultrafilter with
non-convex Tukey and depth spectra is presented, answering questions from [4].
Our construction also provides new models where \mathfrak{u}_\kappa<2^\kappa.
We present an efficient algorithm for checking language equivalence of states
in top-down deterministic finite tree automata (DFTAs). Unlike string automata,
tree automata operate over hierarchical structures, posing unique challenges
for algorithmic analysis. Our approach reduces the equivalence checking problem
to that of checking the solvability of a system of language-theoretic
equations, which specify the behavior of a DFTA. By constructing such a system
of equations and systematically manipulating with it through substitution and
conflict detection rules, we develop a decision procedure that determines
whether two states accept the same tree language. We formally prove the
correctness and termination of the algorithm and establish its worst-case time
complexity as O(n2) under the RAM (Random Access Machine) model of
computation augmented with pointers.
We show that for any i > 0, it is decidable, given a regular language, whether it is expressible in the \Sigma_i[<] fragment of first-order logic FO[<]. This settles a question open since 1971.
Our main technical result relies on the notion of polynomial closure of a class of languages V, that is, finite unions of languages of the form L0a1L1⋯anLn where each ai is a letter and each Li a language of V. We show that if a class V of regular languages with some closure properties (namely, a positive variety) has a decidable separation problem, then so does its polynomial closure Pol(V). The resulting algorithm for Pol(V) has time complexity that is exponential in the time complexity for V and we propose a natural conjecture that would lead to a polynomial time blowup instead.
Corollaries include the decidability of half levels of the dot-depth hierarchy and the group-based concatenation hierarchy.
18 Nov 2024
We introduce exacting cardinals and a strengthening of these, ultraexacting cardinals. These are natural large cardinals defined equivalently as weak forms of rank-Berkeley cardinals, strong forms of Jónsson cardinals, or in terms of principles of structural reflection. However, they challenge commonly held intuition on strong axioms of infinity. We prove that ultraexacting cardinals are consistent with Zermelo-Fraenkel Set Theory with the Axiom of Choice (ZFC) relative to the existence of an I0 embedding. However, the existence of an ultraexacting cardinal below a measurable cardinal implies the consistency of ZFC with a proper class of I0 embeddings, thus challenging the linear-incremental picture of the large cardinal hierarchy. We show that the existence of an exacting cardinal implies that V is not equal to HOD (Gödel's universe of Hereditarily Ordinal Definable sets), showing that these cardinals surpass the current hierarchy of large cardinals consistent with ZFC. We prove that the consistency of ZFC with an exacting cardinal above an extendible cardinal refutes Woodin's HOD Conjecture and Ultimate-L Conjecture. Finally, we establish the consistency of ZFC with the existence of an exacting cardinal above an extendible cardinal from the consistency of ZF with certain large cardinals beyond choice.
07 Oct 2024
We prove an analog of the disintegration theorem for tracial von Neumann algebras in the setting of elementary equivalence rather than isomorphism, showing that elementary equivalence of two direct integrals implies fiberwise elementary equivalence under mild, and necessary, hypotheses. This verifies a conjecture of Farah and Ghasemi. Our argument uses a continuous analog of ultraproducts where an ultrafilter on a discrete index set is replaced by a character on a commutative von Neumann algebra, which is closely related to Keisler randomizations of metric structures. We extend several essential results on ultraproducts, such as Łoś's theorem and countable saturation, to this more general setting.
05 Jun 2025
We study positively closed and strongly positively closed topos-valued models of coherent theories. Positively closed is a global notion (it is defined in terms of all possible outgoing homomorphisms), while strongly positively closed is a local notion (it only concerns the definable sets inside the model). For Set-valued models of coherent theories they coincide.
We prove that if E=Sh(X) for an extremally disconnected Stone space (or equivalently E=Sh(B,τcoh) for a complete Boolean algebra) then i) E-valued types can be realized by E-valued models, and ii) positively closed but not strongly positively closed E-valued models (of coherent theories) exist, yet, there is an alternative local property that characterizes positively closed E-valued models.
A large part of our discussion is given in the context of infinite quantifier geometric logic, dealing with the fragment Lκκg where κ is weakly compact.
The study of modal logic has witnessed tremendous development following the
introduction of Kripke semantics. However, recent developments in programming
languages and type theory have led to a second way of studying modalities,
namely through their categorical semantics. We show how the two correspond.
GFLean is an autoformalisation framework that translates mathematical statements from a controlled natural language, Simplified ForTheL, into formal Lean expressions. It successfully parses and formalizes 42 out of 62 statements from a mathematics textbook chapter, demonstrating a rule-based approach using Grammatical Framework (GF) for linguistic processing and Haskell for Abstract Syntax Tree transformations.
We explore the Weihrauch degree of the problems ``find a bad sequence in a
non-well quasi order'' (BS) and ``find a descending sequence in an
ill-founded linear order'' (DS). We prove that DS is
strictly Weihrauch reducible to BS, correcting our mistaken claim in
[arXiv:2010.03840]. This is done by separating their respective first-order
parts. On the other hand, we show that BS and DS have the
same finitary and deterministic parts, confirming that BS and
DS have very similar uniform computational strength. We prove that
K\"onig's lemma KL and the problem
wList2N,≤ω of enumerating a given non-empty
countable closed subset of 2N are not Weihrauch reducible to
DS or BS, resolving two main open questions raised in
[arXiv:2010.03840]. We also answer the question, raised in [arXiv:1804.10968],
on the existence of a ``parallel quotient'' operator, and study the behavior of
BS and DS under the quotient with some known problems.
07 May 2025
Under CH we construct a partition of Baire space into compact sets,
which is indestructible by countably supported iteration and product of Sacks
forcing of any length, answering a question of Newelski. Further, we present an
in-depth isomorphism-of-names argument for $\text{spec}(\mathfrak{a}_\text{T})
= \{\aleph_1, \mathfrak{c}\}$ in the product-Sacks model. Finally, we prove
that Shelah's ultrapower model for the consistency of $\mathfrak{d} <
\mathfrak{a}alsosatisfies\mathfrak{a} = \mathfrak{a}_\text{T}$. Thus,
consistently \aleph_1 < \mathfrak{d} < \mathfrak{a} = \mathfrak{a}_\text{T}
holds relative to a measurable.
28 Aug 2020
A function F:2ω→2ω is an E0-isomorphism if for all
x,y∈2ω, we have xE0y⟺f(x)E0f(y), where $xE_0y\iff(\exists
a)(\forall n\ge b) x(n)=y(n).IfsuchwitnessesaforxE_0 y$ and for
f(x)E0f(y) depend on each other but not on x, y, then F is called
bi-uniform. It is shown that a homeomorphism of Cantor space which is a
bi-uniform E0-isomorphism can induce only the trivial automorphism of the
Turing degrees.
15 Apr 2023
As several different formal systems with inequivalent syntax may describe
equivalent semantics, it is possible to find `completions' to more expressive
syntaxes that are semantically invariant. Doctrine theory, in the sense of
Lawvere, is the natural categorical framework in which to express completions
for first-order logic. We study the suitability of a fibred generalisation of
the ideal completion of a preorder to act as a completion for doctrines to the
syntax of geometric logic. In contrast to other completions of doctrines
considered in the literature, our completion takes a Grothendieck topology as a
second argument. As a result, the geometric completion is idempotent, as well
as being `semantically invariant' for any doctrine whose models can be
expressed as a category of continuous flat functors, encompassing a wide class
of the most commonly considered doctrines.
We also relate the geometric completion to other completions of doctrines
considered in the literature: first, by studying the behaviour of the geometric
completion when the second argument is omitted, and then by studying the
interaction with those completions of doctrines that complete to a fragment of
geometric logic. Throughout, we reference how these completions of doctrines
yield completions of categories via the syntactic category construction. We
demonstrate that it is equivalent to represent logical theories by either
doctrines or syntactic categories, in so far as they have equivalent
classifying toposes.
01 Aug 2019
An analog of Nadel's effective bound for the continuous Scott rank of metric
structures, developed by Ben Yaacov, Doucha, Nies, and Tsankov, will be
established: Let L be a language of continuous logic with code
L^. Let Ω be a weak modulus of uniform continuity with
code Ω^. Let D be a countable
L-pre-structure. Let Dˉ denote the completion
structure of D. Then $\mathrm{SR}_\Omega(\bar{D}) \leq
\omega_1^{\hat{\mathscr{L}}\oplus\hat{\Omega}\oplus\mathcal{D}}$, the
Church-Kleene ordinal relative to
L^⊕Ω^⊕D.
01 Nov 2023
Solovay's arithmetical completeness theorem states that the modal logic of
provability coincides with the modal logic GL. Hamkins and L\"owe
studied the modal logical aspects of set theoretic multiverse and proved that
the modal logic of forcing is exactly the modal logic S4.2. We
explore the interaction between the notions of provability and forcing in terms
of modal logic. We introduce the bimodal logic PF and prove that the
modal logic of provability and forcing is exactly PF. We also
introduce the bimodal logic PFω and prove that
PFω is exactly the modal logic of provability and forcing true
in ω-models of set theory.
We give a quick survey of the various fixed point theorems in computability theory, partial combinatory algebra, and the theory of numberings, as well as generalizations based on those. We also point out several open problems connected to these.
There are no more papers matching your filters at the moment.