We investigate the Josephson diode effect in an asymmetric SQUID consisting of a sinusoidal Josephson junction formed by a Bi$_2$Te$_2$Se flake and a superconducting Nb nanobridge with a linear and multivalued current-phase relation (CPR). Current-voltage characteristics were measured both in the absence (dc regime) and presence (ac regime) of external microwave irradiation. Our dc measurements reveal only weak critical current asymmetry (i.e. weak Josephson diode effect), while confirming the multivalued behavior of the SQUID. At the same time, the key finding of this work is the observation of strong Shapiro step asymmetry (concerning the dc current direction) in the ac regime at finite magnetic flux. This peculiarity oscillates as a function of magnetic field with the SQUID's periodicity and varies non-monotonically with the increase in microwave power. Our theoretical model shows that the pronounced Shapiro step asymmetry, despite the small diode effect in critical current, arises from the interplay between the sinusoidal and multivalued CPRs of the junctions.

Asymmetric two-junction SQUIDs with different current-phase relations in the two Josephson junctions, involving higher Josephson harmonics, demonstrate a flux-tunable Josephson diode effect (asymmetry between currents flowing in the opposite directions, which can be tuned by the magnetic flux through the interferometer loop). We theoretically investigate influence of junction capacitance and thermal fluctuations on performance of such Josephson diodes. Our main focus is on the "minimal model" with one junction in the SQUID loop possessing the sinusoidal current-phase relation and the other one featuring additional second harmonic. Capacitance generally weakens the diode effect in the resistive branch (R state) of the current-voltage characteristic (CVC) both in the absence and in the presence of external ac irradiation. At the same time, it leads to qualitatively new features of the Josephson diode effect such as asymmetry of the retrapping currents (which are a manifestation of hysteretic CVC). In particular, the limiting case of the single-sided hysteresis becomes accessible. In its turn, thermal fluctuations are known to lead to nonzero average voltages at any finite current, even below the critical value. We demonstrate that in the diode regime, the fluctuation-induced voltage can become strongly (exponentially) asymmetric. In addition, we find asymmetry of the switching currents arising both due to thermal activation and due to Josephson plasma resonances in the presence of ac irradiation.

The structures of the superconducting spin valve (SSV) Fe/\allowbreak Si$_3$N$_4$/\allowbreak Pb/\allowbreak Si$_3$N$_4$/\allowbreak Fe (where Si$_3$N$_4$ is a dielectric insulating layer of controlled thickness) were investigated. The dependence of the magnitude of the SSV effect on the thicknesses of the superconducting (S) and insulating (I) layers was studied. Optimization of the S and I layer thicknesses enabled a complete switching between the normal and superconducting states when the mutual orientation of the magnetizations of the ferromagnetic (F) layers changed from antiparallel to parallel. A maximal SSV effect value of 0.36\,K was achieved in an external magnetic field of 1\,kOe. These results demonstrate that SSV structures with tunable S/F interface transparency controlled by insulating interlayers are promising for achieving a significant magnitude of the effect. This opens new avenues for the development of such systems and their potential applications in spintronic devices.

The article reviews the physics of Anderson localization on random regular graphs (RRG) and its connections to many-body localization (MBL) in disordered interacting systems. Properties of eigenstate and energy level correlations in delocalized and localized phases, as well at criticality, are discussed. In the many-body part, models with short-range and power-law interactions are considered, as well as the quantum-dot model representing the limit of the "most long-range" interaction. Central themes -- which are common to the RRG and MBL problems -- include ergodicity of the delocalized phase, localized character of the critical point, strong finite-size effects, and fractal scaling of eigenstate correlations in the localized phase.

In this paper we will study $R^2$-like inflation in a non-local modification of gravity which contains quadratic in Ricci scalar and Weyl tensor terms with analytic infinite derivative form-factors in the action. It is known that the inflationary solution of the local $R+R^2$ gravity remains a particular exact solution in this model. It was shown earlier that the power spectrum of scalar perturbations generated during inflation in the non-local setup remains the same as in the local $R+R^2$ inflation, whereas the power spectrum of tensor perturbations gets modified due to the non-local Weyl tensor squared term. In the present paper we go beyond 2-point correlators and compute the non-Gaussian parameter $f_{NL}$ related to 3-point correlations generated during inflation, which we found to be different from those in the original local inflationary model and scenarios alike based on a local gravity. We evaluate non-local corrections to the scalar bi-spectrum which give non-zero contributions to squeezed, equilateral and orthogonal configurations. We show that $f_{NL}\sim O(1)$ with an arbitrary sign is achievable in this model based on the choice of form-factors and the scale of non-locality. We present the predictions for the tensor-to-scalar ratio, $r$, and the tensor tilt, $n_t$. In contrast to standard inflation in a local gravity, here the possibility $n_t$>0 is not excluded. Thus, future CMB data can probe non-local behaviour of gravity at high space-time curvatures.

The $R+R^2$, shortly named "$R^2$" ("Starobinsky") inflationary model, represents a fully consistent example of a one-parameter inflationary scenario. This model has a "graceful exit" from inflation and provides a mechanism for subsequent creation and final thermalization of the standard matter. Moreover, it produces a very good fit of the observed spectrum of primordial perturbations. In the present paper we show explicitly that the $R^2$ inflationary spacetime is an exact solution of a range of weakly non-local (quasi-polynomial) gravitational theories, which provide an ultraviolet completion of the $R^2$ theory. These theories are ghost-free, super-renormalizable or finite at quantum level, and perturbatively unitary. Their spectrum consists of the graviton and the scalaron that is responsible for driving the inflation. Notably, any further extension of the spectrum leads to propagating ghost degrees of freedom. We are aimed at presenting a detailed construction of such theories in the so called Weyl basis. Further, we give a special account to the cosmological implications of this theory by considering perturbations during inflation. The highlight of the non-local model is the prediction of a modified, in comparison to a local $R^2$ model, value for the ratio of tensor and scalar power spectra $r$, depending on the parameters of the theory. The relevant parameters are under control to be successfully confronted with existing observational data. Furthermore, the modified $r$ can surely meet future observational constraints.

We consider one-dimensional bosonic chains with a repulsive boson-boson interaction that decays exponentially on large length-scales. This model describes transport of Cooper-pairs in a Josepshon junction array, or transport of magnetic flux quanta in quantum-phase-slip ladders, i.e. arrays of superconducting wires in a ladder-configuration that allow for the coherent tunnelling of flux quanta. In the low-frequency, long wave-length regime these chains can be mapped to an effective model of a one-dimensional elastic field in a disordered potential. The onset of transport in these systems, when biased by external voltage, is described by the standard depinning theory of elastic media in disordered pinning potentials. We numerically study the regimes that are of relevance for quantum-phase-slip ladders. These are (i) very short chains and (ii) the regime of weak disorder. For chains shorter than the typical pinning length, i.e., the Larkin length, the chains reach a saturation regime where the depinning voltage does not depend on the decay length of the repulsive interaction. In the regime of weak disorder we find an emergent correlation length-scale that depends on the disorder strength. For arrays shorter than this length the onset of transport is similar to the clean arrays, i.e., is due to the penetration of solitons into the array. We discuss the depinning scenarios for longer arrays in this regime.

Recent successes in manufacturing of atomically thin graphite samples (graphene) have stimulated intense experimental and theoretical activity. The key feature of graphene is the massless Dirac type of low-energy electron excitations. This gives rise to a number of unusual physical properties of this system distinguishing it from conventional two-dimensional metals. One of the most remarkable properties of graphene is the anomalous quantum Hall effect. It is extremely sensitive to the structure of the system; in particular, it clearly distinguishes single- and double-layer samples. In spite of the impressive experimental progress, the theory of quantum Hall effect in graphene has not been established. This theory is a subject of the present paper. We demonstrate that the Landau level structure by itself is not sufficient to determine the form of the quantum Hall effect. The Hall quantization is due to Anderson localization which, in graphene, is very peculiar and depends strongly on the character of disorder. It is only a special symmetry of disorder that may give rise to anomalous quantum Hall effects in graphene. We analyze the symmetries of disordered single- and double-layer graphene in magnetic field and identify the conditions for anomalous Hall quantization.

We investigate the Josephson diode effect in an asymmetric SQUID consisting of a sinusoidal Josephson junction formed by a Bi$_2$Te$_2$Se flake and a superconducting Nb nanobridge with a linear and multivalued current-phase relation (CPR). Current-voltage characteristics were measured both in the absence (dc regime) and presence (ac regime) of external microwave irradiation. Our dc measurements reveal only weak critical current asymmetry (i.e. weak Josephson diode effect), while confirming the multivalued behavior of the SQUID. At the same time, the key finding of this work is the observation of strong Shapiro step asymmetry (concerning the dc current direction) in the ac regime at finite magnetic flux. This peculiarity oscillates as a function of magnetic field with the SQUID's periodicity and varies non-monotonically with the increase in microwave power. Our theoretical model shows that the pronounced Shapiro step asymmetry, despite the small diode effect in critical current, arises from the interplay between the sinusoidal and multivalued CPRs of the junctions.

Synchronization between the internal dynamics of the superconducting phase in a Josephson junction (JJ) and an external ac signal is a fundamental physical phenomenon, manifesting as constant-voltage Shapiro steps in the current-voltage characteristic. Mathematically, this phase-locking effect is captured by the Resistively Shunted Junction (RSJ) model, an important example of a nonlinear dynamical system. The standard RSJ model considers an overdamped JJ with a sinusoidal (single-harmonic) current-phase relation (CPR) in the current-driven regime with a monochromatic ac component. While this model predicts only integer Shapiro steps, the inclusion of higher Josephson harmonics is known to generate fractional Shapiro steps. In this paper, we show that only two Josephson harmonics in the CPR are sufficient to produce all possible fractional Shapiro steps within the RSJ framework. Using perturbative methods, we analyze the amplitudes of these fractional steps. Furthermore, by introducing a phase shift between the two Josephson harmonics, we reveal an asymmetry between positive and negative fractional steps - a signature of the Josephson diode effect.

We generalize the notion of constant-roll inflation earlier introduced in General Relativity (GR) and $f(R)$ gravity to inflationary models in more general scalar-tensor gravity. A number of novel exact analytic solutions for a FLRW spatially flat cosmological background is found for this case. All forms of the scalar field potential and its coupling to gravity producing the exact de Sitter solution, while the scalar field is varying, are presented. In the particular cases of induced gravity and GR with a non-minimally coupled scalar field, all constant-roll inflationary solutions are found. In the former case they represent power-law inflation, while in the latter case the solution is novel and more complicated. Comparison of scalar perturbations generated during such inflation in induced gravity with observational data shows that the constant-roll parameter should be small, similar to constant-roll inflation in GR and $f(R)$ gravity. Then the solution reduces to the standard slow-roll one with small corrections.

We analyze theoretically the conductivity of Weyl semimetals within the self-consistent Born approximation (SCBA) in the full range of disorder strength, from weak to strong disorder. In the range of intermediate disorder, we find a critical regime which separates the semimetal and diffusion regimes. While the numerical values of the critical exponents are not expected to be exact within the SCBA, the approach allows us to calculate functional dependences of various observables (density of states, quasiparticle broadening, conductivity) in a closed form. This sheds more light on the qualitative behavior of the conductivity and its universal features in disordered Weyl semimetals. In particular, we have found that the vertex corrections in the Kubo formula are of crucial importance in the regime of strong disorder and lead to saturation of the dc conductivity with increasing disorder strength. We have also analyzed the evolution of the optical conductivity with increasing disorder strength, including its scaling properties in the critical regime.

Using redshift space distortion data, we perform model-independent reconstructions of the growth history of matter inhomogeneity in the expanding Universe using two methods: crossing statistics and Gaussian processes. We then reconstruct the corresponding history of the Universe background expansion and fit it to type Ia supernovae data, putting constraints on $(\Omega_\mathrm{m,0},\sigma_{8,0})$. The results obtained are consistent with the concordance flat-$\Lambda$CDM model and General Relativity as the gravity theory given the current quality of the inhomogeneity growth data.

We explore the weak-strong-coupling Bose-Fermi duality in a model of a single-channel integer or fractional quantum Hall edge state with a finite-range interaction. The system is described by a chiral Luttinger liquid with non-linear dispersion of bosonic and fermonic excitations. We use the bosonization, a unitary transformation, and a refermionization to map the system onto that of weakly interacting fermions at low temperature $T$ or weakly interacting bosons at high $T$. We calculate the equilibration rate which is found to scale with temperature as $T^5$ and $T^{14}$ in the high-temperature ("bosonic") and the low-temperature ("fermonic") regimes, respectively. The relaxation rate of a hot particle with the momentum $k$ in the fermonic regime scales as $k^7T^7$.

We study the quantum backreaction from inflationary fluctuations of a very light, non-minimally coupled spectator scalar and show that it is a viable candiate for dark energy. The problem is solved by suitably adapting the formalism of stochastic inflation. This allows us to self-consistently account for the backreaction on the background expansion rate of the Universe where its effects are large. This framework is equivalent to that of semiclassical gravity in which matter vacuum fluctuations are included at the one loop level, but purely quantum gravitational fluctuations are neglected. Our results show that dark energy in our model can be characterized by a distinct effective equation of state parameter (as a function of redshift) which allows for testing of the model at the level of the background.

Emergence of $R^2$ inflation which is the best fit framework for CMB observations till date comes from the attempts to attack the problem of quantization of gravity which in turn have resulted in the trace anomaly discovery. Further developments in trace anomaly and different frameworks aiming to construct quantum gravity indicate an inevitability of non-locality in fundamental physics at small time and length scales. A natural question would be to employ the $R^2$ inflation as a probe for signatures of non-locality in the early Universe physics. Recent advances of embedding $R^2$ inflation in a string theory inspired non-local gravity modification provides very promising theoretical predictions connecting the non-local physics in the early Universe and the forthcoming CMB observations.

We study the dephasing of an individual high-frequency tunneling two-level system (TLS) due to its interaction with an ensemble of low-frequency thermal TLSs which are described by the standard tunneling model (STM). We show that the dephasing by the bath of TLSs explains both the dependence of the Ramsey dephasing rate on an externally applied strain as well as its order of magnitude, as observed in a recent experiment [J. Lisenfeld et al.]. However, the theory based on the STM predicts the Hahn-echo protocol to be much more efficient, yielding too low echo dephasing rates, as compared to the experiment. Also the strain dependence of the echo dephasing rate predicted by the STM does not agree with the measured quadratic dependence, which would fit to a high-frequency white noise environment. We suggest that few fast TLSs which are coupled much more strongly to the strain fields than the usual TLSs of the STM give rise to such a white noise. This explains the magnitude and strong fluctuations of the echo dephasing rate observed in the experiment.

We investigate the zero-temperature phase diagram of the fully frustrated transverse field Ising model on the square lattice both in the classical limit and in the presence of quantum fluctuations. At the classical level (the limit of infinite spin $S$), we find that upon decreasing the transverse field $\Gamma$ this model exhibits a phase transition from the fully polarized state into an eight-fold degenerate translational symmetry breaking state. This phase can be identified to correspond to plaquette order in the dimer language and remains the lowest-energy state in the entire range of fields below the critical one, $\Gamma_c$. The eight-fold degenerate solution which corresponds to columnar order in the dimer language is a saddle point of the classical energy. It is degenerate with the plaquette solution at $\Gamma=0$ and is only slightly higher in energy in the whole interval 0<\Gamma<\Gamma_c. The effect of quantum fluctuations is investigated in the context of a large S expansion both for the plaquette and columnar structures. For this purpose we employ an approximate method allowing to estimate from above the fluctuation-induced correction to the energy of a configuration which at the classical level is a saddle point of the energy, \textit{not} a local minimum. Although the convergence of the $1/S$ expansion in the $\Gamma/J\rightarrow 0$ limit remains an open question, harmonic quantum fluctuations show a clear tendency to overcome the energy difference between the two states and to change the classical picture favoring the columnar order over the plaquette one in a wide parameter range.

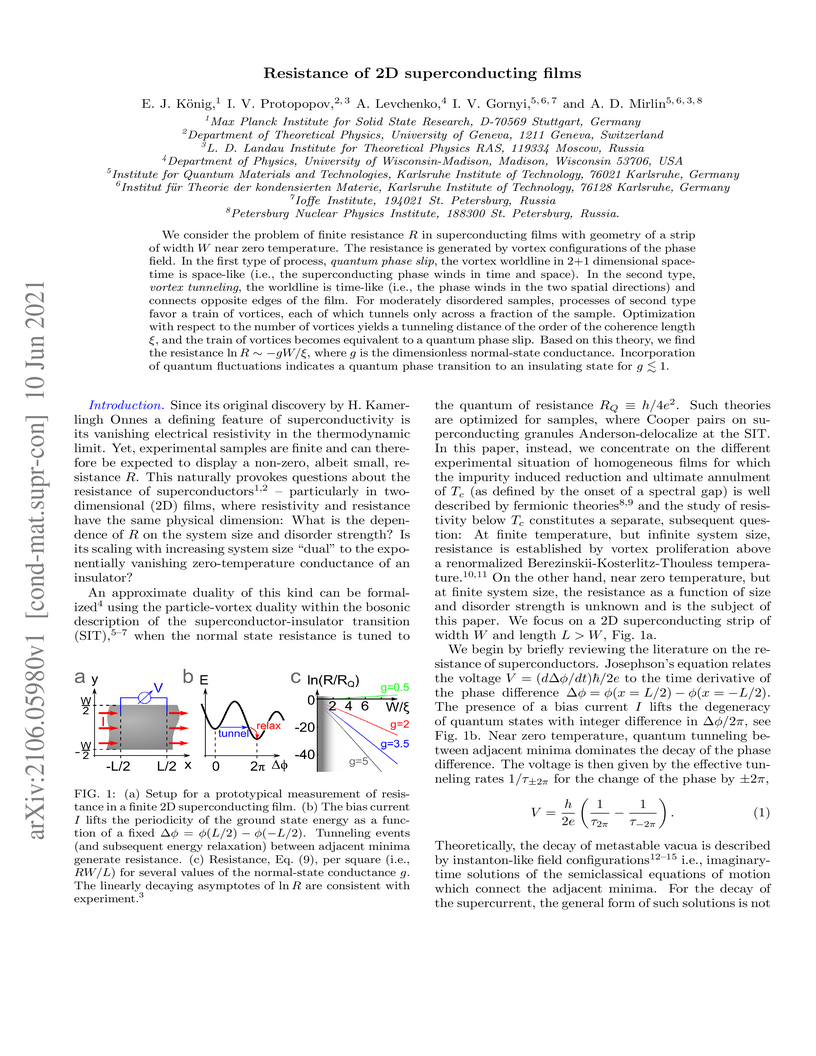
We consider the problem of finite resistance $R$ in superconducting films with geometry of a strip of width $W$ near zero temperature. The resistance is generated by vortex configurations of the phase field. In the first type of process, quantum phase slip, the vortex worldline in 2+1 dimensional space-time is space-like (i.e., the superconducting phase winds in time and space). In the second type, vortex tunneling, the worldline is time-like (i.e., the phase winds in the two spatial directions) and connects opposite edges of the film. For moderately disordered samples, processes of second type favor a train of vortices, each of which tunnels only across a fraction of the sample. Optimization with respect to the number of vortices yields a tunneling distance of the order of the coherence length $\xi$, and the train of vortices becomes equivalent to a quantum phase slip. Based on this theory, we find the resistance $\ln R \sim -g W/\xi$, where $g$ is the dimensionless normal-state conductance. Incorporation of quantum fluctuations indicates a quantum phase transition to an insulating state for $g \lesssim 1$.

We study quench dynamics in an interacting spin chain with a quasi-periodic on-site field, known as the interacting Aubry-André model of many-body localization. Using the time-dependent variational principle, we assess the late-time behavior for chains up to $L = 50$. We find that the choice of periodicity $\Phi$ of the quasi-periodic field influences the dynamics. For $\Phi = (\sqrt{5}-1)/2$ (the inverse golden ratio) and interaction $\Delta = 1$, the model most frequently considered in the literature, we obtain the critical disorder $W_c = 4.8 \pm 0.5$ in units where the non-interacting transition is at $W = 2$. At the same time, for periodicity $\Phi = \sqrt{2}/2$ we obtain a considerably higher critical value, $W_c = 7.8 \pm 0.5$. Finite-size effects on the critical disorder $W_c$ are much weaker than in the purely random case. This supports the enhancement of $W_c$ in the case of a purely random potential by rare "ergodic spots," which do not occur in the quasi-periodic case. Further, the data suggest that the decay of the antiferromagnetic order in the delocalized phase is faster than a power law.