Gaussian states are widely regarded as one of the most relevant classes of continuous-variable (CV) quantum states, as they naturally arise in physical systems and play a key role in quantum technologies. This motivates a fundamental question: given copies of an unknown CV state, how can we efficiently test whether it is Gaussian? We address this problem from the perspective of representation theory and quantum learning theory, characterizing the sample complexity of Gaussianity testing as a function of the number of modes. For pure states, we prove that just a constant number of copies is sufficient to decide whether the state is exactly Gaussian. We then extend this to the tolerant setting, showing that a polynomial number of copies suffices to distinguish states that are close to Gaussian from those that are far. In contrast, we establish that testing Gaussianity of general mixed states necessarily requires exponentially many copies, thereby identifying a fundamental limitation in testing CV systems. Our approach relies on rotation-invariant symmetries of Gaussian states together with the recently introduced toolbox of CV trace-distance bounds.

We investigate the open dynamics of a qubit due to scattering of a single photon in an infinite or semi-infinite waveguide. Through an exact solution of the time-dependent multi-photon scattering problem, we find the qubit's dynamical map. Tools of open quantum systems theory allow us then to discuss the general features of this map, find the corresponding non-Linbladian master equation, and assess in a rigorous way its non-Markovian nature. The qubit dynamics has distinctive features that, in particular, do not occur in emission processes. Two fundamental sources of non-Markovianity are present: the finite width of the photon wavepacket and the time delay for propagation between the qubit and the end of the semi-infinite waveguide.

We investigate the thermoelectric properties of a one-dimensional quantum system in the presence of an external driving. We employ Floquet scattering theory to calculate linear-response stationary thermoelectric figures of merit in a single-channel conductor subjected to a periodically varying delta-like potential barrier. We include a step barrier in one of the leads as a model of a nanoscale inhomogeneous semiconducting system. In the absence of a step barrier, we found that the external driving can strongly enhance the Seebeck coefficient, particularly at low temperatures, with a relative increase with respect to the static condition reaching up to 200% at large frequencies. In the presence of a step barrier, we found that the thermoelectric Onsager coefficient for the driven case is also enhanced with respect to the static case with a significant effect at low temperatures when the chemical potential is within the gap of the semiconductor. Our results demonstrate that external driving can be used to tune and enhance the thermoelectric capabilities of low-electron-density nanodevices.

We extend the concept of superadiabatic dynamics, or transitionless quantum driving, to quantum open systems whose evolution is governed by a master equation in the Lindblad form. We provide the general framework needed to determine the control strategy required to achieve superadiabaticity. We apply our formalism to two examples consisting of a two-level system coupled to environments with time-dependent bath operators.

Ultrastrong coupling may allow faster operations for the development of quantum technologies at the expenses of increased sensitivity to new kind of intrinsic errors. We study state transfer in superconducting circuit QED architectures in the ultrastrong coupling regime. Using optimal control methods we find a protocol resilient to the main source of errors, coming from the interplay of the dynamical Casimir effect with cavity losses.

We present a novel mapping for studying 2D many-body quantum systems by solving an effective, one-dimensional long-range model in place of the original two-dimensional short-range one. In particular, we address the problem of choosing an efficient mapping from the 2D lattice to a 1D chain that optimally preserves the locality of interactions within the TN structure. By using Matrix Product States (MPS) and Tree Tensor Network (TTN) algorithms, we compute the ground state of the 2D quantum Ising model in transverse field with lattice size up to $64\times64$, comparing the results obtained from different mappings based on two space-filling curves, the snake curve and the Hilbert curve. We show that the locality-preserving properties of the Hilbert curve leads to a clear improvement of numerical precision, especially for large sizes, and turns out to provide the best performances for the simulation of 2D lattice systems via 1D TN structures.

Owing to its superconducting properties, Niobium (Nb) is an excellent candidate material for superconducting electronics and applications in quantum technology. Here we perform scanning tunneling microscopy and spectroscopy experiments on Nb films covered by a thin gold (Au) film. We investigate the minigap structure of the proximitized region and provide evidence for a highly transparent interface between Nb and Au, beneficial for device applications. Imaging of Abrikosov vortices in presence of a perpendicular magnetic field is reported. The data show vortex pinning by the granular structure of the polycrystalline Au film. Our results show robust and homogeneous superconducting properties of thin Nb film in the presence of a gold capping layer. The Au film not only protects the Nb from surface oxidation but also preserves its excellent superconducting properties.

A generalized multi-parameter Hong-Ou-Mandel interferometer is presented which extends the conventional "Mandel dip" configuration to the case where a symmetric biphoton source is used to monitor the contemporary presence of k independent time-delays. Our construction results in a two-input/two-output setup, obtained by concatenating 50:50 beam splitters with a collection of adjustable achromatic wave-plates. For k=1,2 and k=4 explicit examples can be exhibited that prove the possibility of uniquely linking the zero value of the coincidence counts registered at the output of the interferometer, with the contemporary absence of all the time-delays. Interestingly enough the same result cannot be extended to k=3. Besides, the sensitivity of the interferometer is analyzed when the time-delays are affected by the fluctuations over time-scales that are larger than the inverse of the frequency of the pump used to generate the biphoton state.

By using worldline and diagrammatic quantum Monte Carlo techniques, matrix product state and a variational approach à la Feynman, we investigate the equilibrium properties and relaxation features of a quantum system of $N$ spins antiferromagnetically interacting with each other, with strength $J$, and coupled to a common bath of bosonic oscillators, with strength $\alpha$. We show that, in the Ohmic regime, a Beretzinski-Thouless-Kosterlitz quantum phase transition occurs. While for $J=0$ the critical value of $\alpha$ decreases asymptotically with $1/N$ by increasing $N$, for nonvanishing $J$ it turns out to be practically independent on $N$, allowing to identify a finite range of values of $\alpha$ where spin phase coherence is preserved also for large $N$. Then, by using matrix product state simulations, and the Mori formalism and the variational approach à la Feynman jointly, we unveil the features of the relaxation, that, in particular, exhibits a non monotonic dependence on the temperature reminiscent of the Kondo effect. For the observed quantum phase transition we also establish a criterion analogous to that of the metal-insulator transition in solids.

We derive an exact master equation that captures the dynamics of a quadratic quantum system linearly coupled to a Gaussian environment. Unlike previous approaches, our formulation applies universally to both bosonic and fermionic reservoirs, and remains valid even in the presence of initial system-environment correlations. Remarkably, the master equation is written without employing field objects, path integrals, or involved superoperators. As a result, it shows an explicit and extremely compact dependence on the dressed environment correlation function: this allows us to state exactly how sequential virtual interactions between the system and the environment eventually lead to non-Markovian evolution. In the weak-coupling limit, this dependence facilitates a straightforward recovery of the well-known Redfield equation at second order in the coupling.

We introduce a novel frequency-dependent incoherent pump scheme with a square-shaped spectrum as a way to study strongly correlated photons in arrays of coupled nonlinear resonators. This scheme can be implemented via a reservoir of population-inverted two-level emitters with a broad distribution of transition frequencies. Our proposal is predicted to stabilize a non-equilibrium steady state sharing important features with a zero-temperature equilibrium state with a tunable chemical potential. We confirm the efficiency of our proposal for the Bose-Hubbard model by computing numerically the steady state for finite system sizes: first, we predict the occurrence of a sequence of incompressible Mott-Insulator-like states with arbitrary integer densities presenting strong robustness against tunneling and losses. Secondly, for stronger tunneling amplitudes or non-integer densities, the system enters a coherent regime analogous to the superfluid state. In addition to an overall agreement with the zero-temperature equilibrium state, exotic non-equilibrium processes leading to a finite entropy generation are pointed out in specific regions of parameter space. The equilibrium ground state is shown to be recovered by adding frequency-dependent losses. The promise of this improved scheme in view of quantum simulation of the zero temperature many-body physics is highlighted.

Quantum optical systems are typically affected by two types of noise: photon loss and dephasing. Despite extensive research on each noise process individually, a comprehensive understanding of their combined effect is still lacking. A crucial problem lies in determining the values of loss and dephasing for which the resulting loss-dephasing channel is anti-degradable, implying the absence of codes capable of correcting its effect or, alternatively, capable of enabling quantum communication. A conjecture in [Quantum 6, 821 (2022)] suggested that the bosonic loss-dephasing channel is anti-degradable if and only if the loss is above $50\%$. In this paper we refute this conjecture, specifically proving that for any value of the loss, if the dephasing is above a critical value, then the bosonic loss-dephasing channel is anti-degradable. While our result identifies a large parameter region where quantum communication is not possible, we also prove that if two-way classical communication is available, then quantum communication -- and thus quantum key distribution -- is always achievable, even for high values of loss and dephasing.

We study several parasitic effects on the implementation of a Josephson radiation comb generator (JRCG) based on a dc superconducting quantum interference device (SQUID) driven by an external magnetic field. This system can be used as a radiation generator similarly to what is done in optics and metrology, and allows one to generate up to several hundreds of harmonics of the driving frequency. First we take into account how assuming a finite loop geometrical inductance and junction capacitance in each SQUID may alter the operation of this device. Then, we estimate the effect of imperfections in the fabrication of an array of SQUIDs, which is an unavoidable source of errors in practical situations. We show that the role of the junction capacitance is in general negligible, whereas the geometrical inductance has a beneficial effect on the performance of the device. The errors on the areas and junction resistance asymmetries may deteriorate the performance, but their effect can be limited up to a large extent with a suitable choice of fabrication parameters.

We report on a quantum thermodynamic method to purify a qubit on a quantum processing unit (QPU) equipped with (nearly) identical qubits. Our starting point is a three qubit design that emulates the well known two qubit swap engine. Similar to standard fridges, the method would allow to cool down a qubit at the expense of heating two other qubits. A minimal modification thereof leads to a more practical three qubit design that allows for enhanced refrigeration tasks, such as increasing the purity of one qubit at the expense of decreasing the purity of the other two. The method is based on the application of properly designed quantum circuits, and can therefore be run on any gate model quantum computer. We implement it on a publicly available superconducting qubit based QPU, and observe a purification capability down to 200 mK. We identify gate noise as the main obstacle towards practical application for quantum computing.

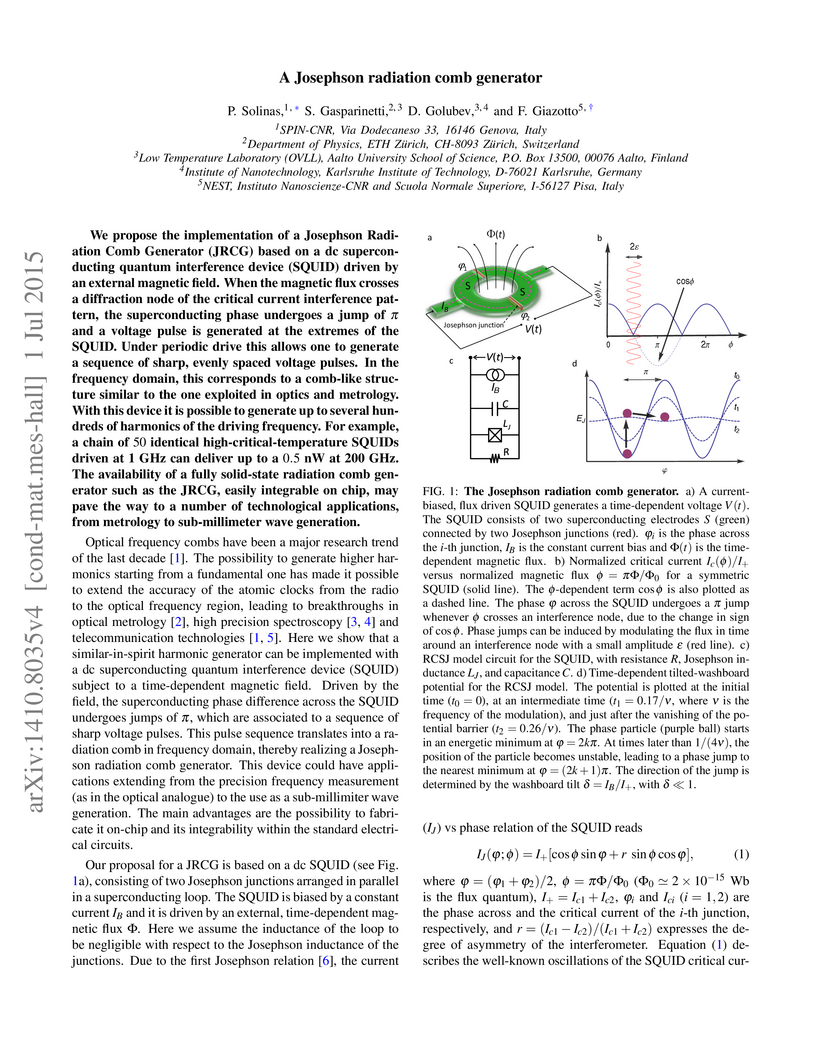
We propose the implementation of a Josephson Radiation Comb Generator (JRCG) based on a dc superconducting quantum interference device (SQUID) driven by an external magnetic field. When the magnetic flux crosses a diffraction node of the critical current interference pattern, the superconducting phase undergoes a jump of $\pi$ and a voltage pulse is generated at the extremes of the SQUID. Under periodic drive this allows one to generate a sequence of sharp, evenly spaced voltage pulses. In the frequency domain, this corresponds to a comb-like structure similar to the one exploited in optics and metrology. With this device it is possible to generate up to several hundreds of harmonics of the driving frequency. For example, a chain of $50$ identical high-critical-temperature SQUIDs driven at 1 GHz can deliver up to a $0.5$ nW at 200 GHz. The availability of a fully solid-state radiation comb generator such as the JRCG, easily integrable on chip, may pave the way to a number of technological applications, from metrology to sub-millimeter wave generation.

Optical frequency combs (FCs), that establish a rigid phase-coherent link between the microwave and optical domains of the electromagnetic spectrum, are emerging as a key high-precision tools for the development of quantum technology platforms. These include potential applications for communication, computation, information, sensing and metrology, and can extend from the near-infrared with micro-resonator combs, up to the technologically attractive terahertz (THz) frequency range, with powerful and miniaturized quantum cascade laser (QCL) FCs. The recently discovered ability of the QCLs to produce a harmonic frequency comb (HFC), a FC with large intermodal spacings, has attracted new interest in these devices for both applications and fundamental physics, particularly for the generation of THz tones of high spectral purity for high data rate wireless communication networks, for radiofrequency arbitrary waveform synthesis, and for the development of quantum key distributions. The controlled generation of harmonic states of a specific order remains, however, elusive in THz QCLs. Here we devise a strategy to obtain broadband HFC emission of a pre-defined order in QCL, by design. By patterning n regularly spaced defects on the top-surface of a double-metal Fabry-Perot QCL, we demonstrate harmonic comb emission with modes spaced by (n+1) free spectral range and with a record optical power/mode of ~270 $\mu W$.

Achieving good quality Ohmic contacts to van der Waals materials is a challenge, since at the interface between metal and van der Waals material, different conditions can occur, ranging from the presence of a large energy barrier between the two materials to the metallization of the layered material below the contacts. In black phosphorus (bP), a further challenge is its high reactivity to oxygen and moisture, since the presence of uncontrolled oxidation can substantially change the behavior of the contacts. In this study, we investigate the influence of the metal used for the contacts to bP against the variability between different flakes and different samples, using three of the most used metals as contacts: Chromium, Titanium, and Nickel. Using the transfer length method, from an analysis of ten devices, both at room temperature and at low temperature, Ni results to be the best metal for Ohmic contacts to bP, providing the lowest contact resistance and minimum scattering between different devices. Moreover, we investigate the gate dependence of the current-voltage characteristics of these devices. In the accumulation regime, we observe good linearity for all metals investigated.

The phase of an optical field inside a linear amplifier is widely known to diffuse with a diffusion coefficient that is inversely proportional to the photon number. The same process occurs in lasers which limits its intrinsic linewidth and makes the phase uncertainty difficult to calculate. The most commonly used simplification is to assume a narrow photon-number distribution for the optical field (which we call the small-noise approximation). For coherent light, this condition is determined by the average photon number. The small-noise approximation relies on (i) the input to have a good signal-to-noise ratio, and (ii) that such a signal-to-noise ratio can be maintained throughout the amplification process. Here we ask: For a coherent input, how many photons must be present in the input to a quantum linear amplifier for the phase noise at the output to be amenable to a small-noise analysis? We address these questions by showing how the phase uncertainty can be obtained without recourse to the small-noise approximation. It is shown that for an ideal linear amplifier (i.e. an amplifier most favourable to the small-noise approximation), the small-noise approximation breaks down with only a few photons on average. Interestingly, when the input strength is increased to tens of photons, the small-noise approximation can be seen to perform much better and the process of phase diffusion permits a small-noise analysis. This demarcates the limit of the small-noise assumption in linear amplifiers as such an assumption is less true for a nonideal amplifier.

We study two different models of optomechanical systems where a temperature gradient between two radiation baths is exploited for inducing self-sustained coherent oscillations of a mechanical resonator. Viewed from a thermodynamic perspective, such systems represent quantum instances of self-contained thermal machines converting heat into a periodic mechanical motion and thus they can be interpreted as nano-scale analogues of macroscopic piston engines. Our models are potentially suitable for testing fundamental aspects of quantum thermodynamics in the laboratory and for applications in energy efficient nanotechnology.

The notion of weak-degradability of quantum channels is introduced by generalizing the degradability definition given by Devetak and Shor. Exploiting the unitary equivalence with beam-splitter/amplifier channels we then prove that a large class of one-mode Bosonic Gaussian channels are either weakly degradable or anti-degradable. In the latter case this implies that their quantum capacity Q is null. In the former case instead, this allows us to establish the additivity of the coherent information for those maps which admit unitary representation with single-mode pure environment.