We consider a finite-dimensional oscillatory integral which provides a "finite-dimensional model" for analytically continued $SU(2)$ Chern-Simons theory on closed 3-manifolds that are described by plumbing trees. This model allows an efficient description of Stokes phenomenon for perturbative expansions in Chern-Simons theory around classical solutions - $SL(2,\mathbb{C})$ flat connections. Moreover, the Stokes coefficients can be categorified, i.e. promoted to graded vector spaces, in terms of this finite-dimensional model. At least naively, the categorification gives BPS spectrum of 5d maximally supersymmetric Yang-Mills theory on the 3-manifold times a line with appropriate boundary conditions. We also comment on necessity of taking into account "flat connections at infinity" to capture Stokes phenomenon for certain 3-manifolds.

Inflationary perturbations are approximately Gaussian and deviations from Gaussianity are usually calculated using in-in perturbation theory. This method, however, fails for unlikely events on the tail of the probability distribution: in this regime non-Gaussianities are important and perturbation theory breaks down for $|\zeta| \gtrsim |f_{\rm \scriptscriptstyle NL}|^{-1}$. In this paper we show that this regime is amenable to a semiclassical treatment, $\hbar \to 0$. In this limit the wavefunction of the Universe can be calculated in saddle-point, corresponding to a resummation of all the tree-level Witten diagrams. The saddle can be found by solving numerically the classical (Euclidean) non-linear equations of motion, with prescribed boundary conditions. We apply these ideas to a model with an inflaton self-interaction $\propto \lambda \dot\zeta^4$. Numerical and analytical methods show that the tail of the probability distribution of $\zeta$ goes as $\exp(-\lambda^{-1/4}\zeta^{3/2})$, with a clear non-perturbative dependence on the coupling. Our results are relevant for the calculation of the abundance of primordial black holes.

Four-dimensional gauge theories with matter can have regions in parameter space, often dubbed conformal windows, where they flow in the infrared to non-trivial conformal field theories. It has been conjectured that conformality can be lost because of merging of two nearby fixed points that move into the complex plane, and that a walking dynamics governed by scaling dimensions of operators defined at such complex fixed points can occur. We find controlled, parametrically weakly coupled, and ultraviolet-complete 4D gauge theories that explicitly realize this scenario. We show how the walking dynamics is controlled by the coupling of a double-trace operator that crosses marginality. The walking regime ends when the renormalization group flow of this coupling leads to a (weak) first-order phase transition with Coleman-Weinberg symmetry breaking. A light dilaton-like scalar particle appears in the spectrum, but it is not parametrically lighter than the other excitations.

We study static brane configurations in the bulk background of the topological black holes in asymptotically flat spacetime. We find that such configurations are possible even for flat black hole horizon, unlike the AdS black hole case. We construct the brane world model with an orbifold structure S^1/Z_2 in such bulk background. We also study massless bulk scalar field.

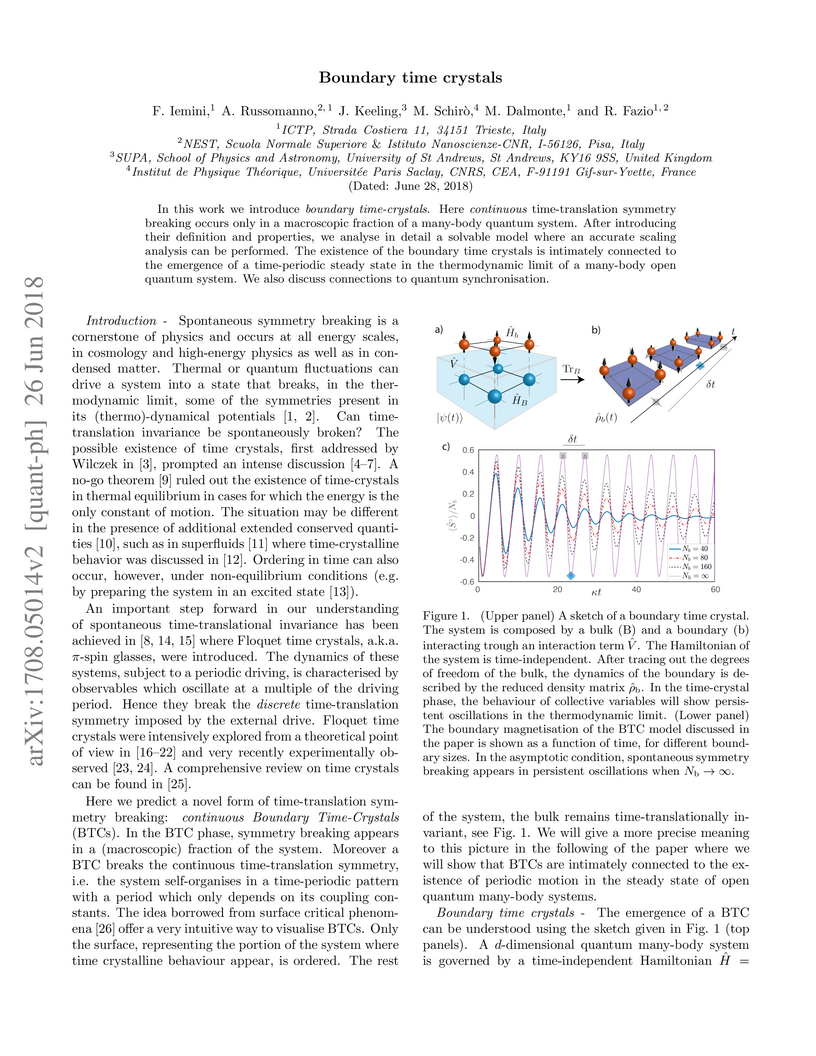
In this work we introduce {\it boundary time-crystals}. Here {\it continuous} time-translation symmetry breaking occurs only in a macroscopic fraction of a many-body quantum system. After introducing their definition and properties, we analyse in detail a solvable model where an accurate scaling analysis can be performed. The existence of the boundary time crystals is intimately connected to the emergence of a time-periodic steady state in the thermodynamic limit of a many-body open quantum system. We also discuss connections to quantum synchronisation.

Simulated Quantum Annealing (SQA), that is emulating a Quantum Annealing (QA) dynamics on a classical computer by a Quantum Monte Carlo whose parameters are changed during the simulation, is a well established computational strategy to cope with the exponentially large Hilbert space. It has enjoyed some early successes but has also raised more recent criticisms. Here we investigate, on the paradigmatic case of a one-dimensional transverse field Ising chain, two issues related to SQA in its Path-Integral implementation: the question of Monte Carlo vs physical (Schrödinger) dynamics and the issue of the imaginary-time continuum limit to eliminate the Trotter error. We show that, while a proper time-continuum limit is able to restitute the correct Kibble-Zurek scaling of the residual energy $\varepsilon_\mathrm{res}(\tau)\sim \tau^{-1/2}$ for the ordered case --- $\tau$ being the total annealing time ---, the presence of disorder leads to a characteristic sampling crisis for a large number of Trotter time-slices, in the low-temperature ordered phase. Such sampling problem, in turn, leads to SQA results which are apparently unrelated to the coherent Schrödinger QA even at intermediate $\tau$.

We study the quantum Fisher information (QFI) and, thus, the multipartite entanglement structure of thermal pure states in the context of the Eigenstate Thermalization Hypothesis (ETH). In both the canonical ensemble and the ETH, the quantum Fisher information may be explicitly calculated from the response functions. In the case of ETH, we find that the expression of the QFI bounds the corresponding canonical expression from above. This implies that although average values and fluctuations of local observables are indistinguishable from their canonical counterpart, the entanglement structure of the state is starkly different; with the difference amplified, e.g., in the proximity of a thermal phase transition. We also provide a state-of-the-art numerical example of a situation where the quantum Fisher information in a quantum many-body system is extensive while the corresponding quantity in the canonical ensemble vanishes. Our findings have direct relevance for the entanglement structure in the asymptotic states of quenched many-body dynamics.

The competition between interactions and dissipative processes in a quantum many-body system can drive phase transitions of different order. Exploiting a combination of cluster methods and quantum trajectories, we show how the systematic inclusion of (classical and quantum) nonlocal correlations at increasing distances is crucial to determine the structure of the phase diagram, as well as the nature of the transitions in strongly interacting spin systems. In practice, we focus on the paradigmatic dissipative quantum Ising model: in contrast to the non-dissipative case, its phase diagram is still a matter of debate in the literature. When dissipation acts along the interaction direction, we predict important quantitative modifications of the position of the first-order transition boundary. In the case of incoherent relaxation in the field direction, our approach confirms the presence of a second-order transition, while does not support the possible existence of multicritical points. Potentially, these results can be tested in up-to date quantum simulators of Rydberg atoms.

Entanglement asymmetry is a measure of symmetry breaking in quantum subsystems, inspired by quantum information theory, particularly suited to study out-of-equilibrium states. We study the entanglement asymmetry of a class of excited "coherent states" in conformal quantum field theories with a U(1) symmetry, employing Euclidean path-integral methods with topological symmetry defects and the replica formalism. We compute, at leading order in perturbation theory, the asymmetry for a variety of subsystems, including finite spherical subregions in flat space, in finite volume, and at positive temperature. We also study its Lorentzian time evolution, showcasing the dynamical restoration of the symmetry due to thermalization, as well as the presence of a quantum Mpemba effect. Our results are universal, and apply in any number of dimensions. We also show that the perturbative entanglement asymmetry is related to the Fisher information metric, which has a known holographic dual called Hollands-Wald canonical energy, and that it is captured by the AdS bulk charge contained in the entanglement wedge.

We revisit the issue of the limit on the scale of Left-Right symmetry breaking. We focus on the minimal SU(2)_L x SU(2)_R x U(1)_B-L gauge theory with the seesaw mechanism and discuss the two possibilities of defining Left-Right symmetry as parity or charge conjugation. In the commonly adopted case of parity, we perform a complete numerical study of the quark mass matrices and the associated left and right mixing matrices without any assumptions usually made in the literature about the ratio of vacuum expectation values. We find that the usual lower limit on the mass of the right-handed gauge boson from the K mass difference, M_WR>2.5TeV, is subject to a possible small reduction due to the difference between right and left Cabibbo angles. In the case of charge conjugation the limit on M_WR is somewhat more robust. However, the more severe bounds from CP-violating observables are absent in this case. In fact, the free phases can also resolve the present mild discrepancy between the Standard Model and CP-violation in the $B$-sector. Thus, even in the minimal case, both charged and neutral gauge bosons may be accessible at the Large Hadron Collider with spectacular signatures of lepton number violation.

To gain insight into the mechanisms behind machine learning methods, it is crucial to establish connections among the features describing data points. However, these correlations often exhibit a high-dimensional and strongly nonlinear nature, which makes them challenging to detect using standard methods. This paper exploits the entanglement between intrinsic dimensionality and correlation to propose a metric that quantifies the (potentially nonlinear) correlation between high-dimensional manifolds. We first validate our method on synthetic data in controlled environments, showcasing its advantages and drawbacks compared to existing techniques. Subsequently, we extend our analysis to large-scale applications in neural network representations. Specifically, we focus on latent representations of multimodal data, uncovering clear correlations between paired visual and textual embeddings, whereas existing methods struggle significantly in detecting similarity. Our results indicate the presence of highly nonlinear correlation patterns between latent manifolds.

Peer-review system has long been relied upon for bringing quality research to the notice of the scientific community and also preventing flawed research from entering into the literature. The need for the peer-review system has often been debated as in numerous cases it has failed in its task and in most of these cases editors and the reviewers were thought to be responsible for not being able to correctly judge the quality of the work. This raises a question "Can the peer-review system be improved?" Since editors and reviewers are the most important pillars of a reviewing system, we in this work, attempt to address a related question - given the editing/reviewing history of the editors or re- viewers "can we identify the under-performing ones?", with citations received by the edited/reviewed papers being used as proxy for quantifying performance. We term such review- ers and editors as anomalous and we believe identifying and removing them shall improve the performance of the peer- review system. Using a massive dataset of Journal of High Energy Physics (JHEP) consisting of 29k papers submitted between 1997 and 2015 with 95 editors and 4035 reviewers and their review history, we identify several factors which point to anomalous behavior of referees and editors. In fact the anomalous editors and reviewers account for 26.8% and 14.5% of the total editors and reviewers respectively and for most of these anomalous reviewers the performance degrades alarmingly over time.

Cosmic voids, the less dense patches of the Universe, are promising laboratories to extract cosmological information. Thanks to their unique low density character, voids are extremely sensitive to diffuse components such as neutrinos and dark energy, and represent ideal environments to study modifications of gravity, where the effects of such modifications are expected to be more prominent. Robust void-related observables, including for example redshift-space distortions (RSD) and weak lensing around voids, are a promising way to chase and test new physics. Cosmological analysis of the large-scale structure of the Universe predominantly relies on the high density regions. Current and upcoming surveys are designed to optimize the extraction of cosmological information from these zones, but leave voids under-exploited. A dense, large area spectroscopic survey with imaging capabilities is ideal to exploit the power of voids fully. Besides helping illuminate the nature of dark energy, modified gravity, and neutrinos, this survey will give access to a detailed map of under-dense regions, providing an unprecedented opportunity to observe and study a so far under-explored galaxy population.

We explore a novel interpretation of Symmetry Topological Field Theories (SymTFTs) as theories of gravity, proposing a holographic duality where the bulk SymTFT (with the gauging of a suitable Lagrangian algebra) is dual to the universal effective field theory (EFT) that describes spontaneous symmetry breaking on the boundary. We test this conjecture in various dimensions and with many examples involving different continuous symmetry structures, including non-Abelian and non-invertible symmetries, as well as higher groups. For instance, we find that many Abelian SymTFTs are dual to free theories of Goldstone bosons or generalized Maxwell fields, while non-Abelian SymTFTs relate to non-linear sigma models with target spaces defined by the symmetry groups. We also extend our analysis to include the non-invertible $\mathbb{Q}/\mathbb{Z}$ axial symmetry, finding it to be dual to axion-Maxwell theory, and a non-Abelian 2-group structure in four dimensions, deriving a new parity-violating interaction that has implications for the low-energy dynamics of U(N) QCD.

Here we review the present status of modelling of and searching for primordial non-Gaussianity of cosmological perturbations. After introducing the models for non-Gaussianity generation during inflation, we discuss the search for non-Gaussian signatures in the Cosmic Microwave Background and in the Large-Scale Structure of the Universe.

These notes consist of a study of special Lagrangian submanifolds of Calabi-Yau manifolds and their moduli spaces. The particular case of three dimensions, important in string theory, allows us to introduce the notion of gerbes. These offer an appropriate language for describing many significant features of the Strominger-Yau-Zaslow approach to mirror symmetry.

We apply numerical conformal bootstrap techniques to the four-point function of a Weyl spinor in 4d non-supersymmetric CFTs. We find universal bounds on operator dimensions and OPE coefficients, including bounds on operators in mixed symmetry representations of the Lorentz group, which were inaccessible in previous bootstrap studies. We find discontinuities in some of the bounds on operator dimensions, and we show that they arise due to a generic yet previously unobserved fake primary effect, which is related to the existence of poles in conformal blocks. We show that this effect is also responsible for similar discontinuities found in four-fermion bootstrap in 3d, as well as in the mixed-correlator analysis of the 3d Ising CFT. As an important byproduct of our work, we develop a practical technology for numerical approximation of general 4d conformal blocks.

In arXiv:1407.7580 a mechanism to fix the closed string moduli in a de Sitter minimum was proposed: a D-term potential generates a linear relation between the volumes of two rigid divisors which in turn produces at lower energies a race-track potential with de Sitter minima at exponentially large volume. In this paper, we systematically search for implementations of this mechanism among all toric Calabi-Yau hypersurfaces with $h^{1,1}\leq 4$ from the Kreuzer-Skarke list. For these, topological data can be computed explicitly allowing us to find the subset of three-folds which have two rigid toric divisors that do not intersect each other and that are orthogonal to $h^{1,1}-2$ independent four-cycles. These manifolds allow to find D7-brane configurations compatible with the de Sitter uplift mechanism and we find an abundance of consistent choices of D7-brane fluxes inducing D-terms leading to a de Sitter minimum. Finally, we work out a couple of models in detail, checking the global consistency conditions and computing the value of the potential at the minimum.