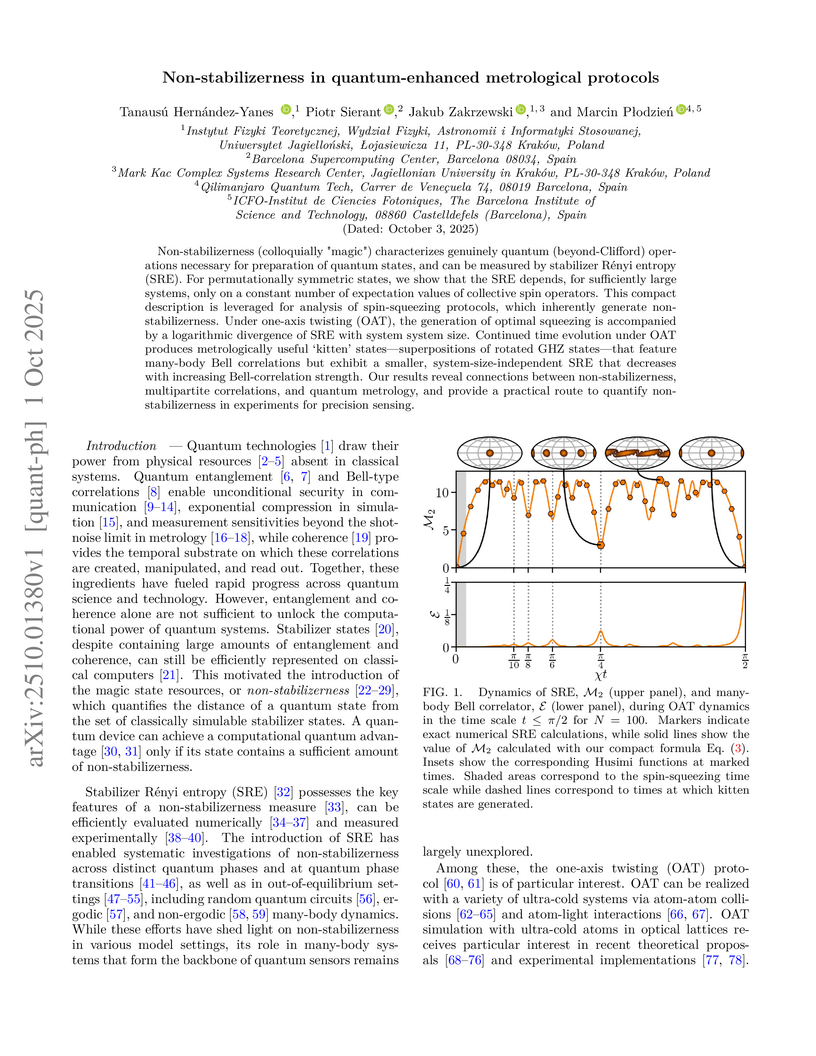
Non-stabilizerness (colloquially "magic") characterizes genuinely quantum (beyond-Clifford) operations necessary for preparation of quantum states, and can be measured by stabilizer Rényi entropy (SRE). For permutationally symmetric states, we show that the SRE depends, for sufficiently large systems, only on a constant number of expectation values of collective spin operators. This compact description is leveraged for analysis of spin-squeezing protocols, which inherently generate non-stabilizerness. Under one-axis twisting (OAT), the generation of optimal squeezing is accompanied by a logarithmic divergence of SRE with system system size. Continued time evolution under OAT produces metrologically useful "kitten" states-superpositions of rotated GHZ states-that feature many-body Bell correlations but exhibit a smaller, system-size-independent SRE that decreases with increasing Bell-correlation strength. Our results reveal connections between non-stabilizerness, multipartite correlations, and quantum metrology, and provide a practical route to quantify non-stabilizerness in experiments for precision sensing.

Statistical mechanics provides a framework for describing the physics of large, complex many-body systems using only a few macroscopic parameters to determine the state of the system. For isolated quantum many-body systems, such a description is achieved via the eigenstate thermalization hypothesis (ETH), which links thermalization, ergodicity and quantum chaotic behavior. However, tendency towards thermalization is not observed at finite system sizes and evolution times in a robust many-body localization (MBL) regime found numerically and experimentally in the dynamics of interacting many-body systems at strong disorder. Although the phenomenology of the MBL regime is well-established, the central question remains unanswered: under what conditions does the MBL regime give rise to an MBL phase in which the thermalization does not occur even in the asymptotic limit of infinite system size and evolution time? This review focuses on recent numerical investigations aiming to clarify the status of the MBL phase, and it establishes the critical open questions about the dynamics of disordered many-body systems. Persistent finite size drifts towards ergodicity consistently emerge in spectral properties of disordered many-body systems, excluding naive single-parameter scaling hypothesis and preventing comprehension of the status of the MBL phase. The drifts are related to tendencies towards thermalization and non-vanishing transport observed in the dynamics of many-body systems, even at strong disorder. These phenomena impede understanding of microscopic processes at the ETH-MBL crossover. Nevertheless, the abrupt slowdown of dynamics with increasing disorder strength suggests the proximity of the MBL phase. This review concludes that the questions about thermalization and its failure in disordered many-body systems remain a captivating area open for further explorations.

We consider the dynamics in the one-dimensional quantum Ising model in which each spin coherently interacts with its phononic mode. The model is motivated by quantum simulators based on Rydberg atoms in tweezers or trapped ions. The configuration of two domain walls simulates the particle-antiparticle connecting string. We concentrate on the effect the local vibrations have on the dynamics of this initial state. Our study supplements recent investigations of string breaking, traditionally studied within quantum chromodynamics (QCD), to quantum many-body systems. Two regimes are identified depending on the strength of the coupling with local vibrations. For weak coupling, the string breaking is slowed down as compared to the dynamics in an isolated Ising string. The strong coupling leads to complicated dynamics in which the domain wall character of excitation is dissolved among many coupled states.

Time crystals are time-periodic self-organized structures postulated by Frank Wilczek in 2012. While the original concept was strongly criticized, it stimulated at the same time an intensive research leading to propositions and experimental verifications of discrete (or Floquet) time crystals -- the structures that appear in the time domain due to spontaneous breaking of discrete time translation symmetry. The struggle to observe discrete time crystals is reviewed here together with propositions that generalize this concept introducing condensed matter like physics in the time domain. We shall also revisit the original Wilczek's idea and review strategies aimed at spontaneous breaking of continuous time translation symmetry.

Nonstabilizerness, also known as quantum magic, quantifies the deviation of quantum states from stabilizer states, capturing the complexity necessary for quantum computational advantage. In this study, we investigate the dynamics of quantum magic in disordered many-body localized (MBL) systems using the stabilizer Rényi entropy (SRE). Leveraging a phenomenological description based on the $\ell$-bit model, we analytically and numerically demonstrate that interactions profoundly influence magic spreading, inducing a power-law growth of SRE that markedly contrasts with the rapid saturation observed in ergodic systems. We validate our theoretical predictions through numerical simulations of the disordered transverse-field Ising model, showing excellent agreement across various disorder strengths, system sizes, and initial states. Additionally, we uncover a universal relationship between SRE and entanglement entropy, revealing their common scaling in the MBL regime independent of disorder strength and system size. Our results offer critical insights into the interplay of disorder, interactions, and complexity in quantum many-body systems.

Ergodic isolated quantum many-body systems satisfy the eigenstate thermalization hypothesis (ETH), i.e., the expectation values of local observables in the system's eigenstates approach the predictions of the microcanonical ensemble. However, the ETH does not specify what happens to expectation values of local observables within an energy window when the average over disorder realizations is taken. As a result, the expectation values of local observables can be distributed over a relatively wide interval and may exhibit nontrivial structure, as shown in [Phys. Rev. B \textbf{104}, 214201 (2021)] for a quasiperiodic disordered system for site-resolved magnetization. We argue that the non-Gaussian form of this distribution may \textit{falsely} suggest non-ergodicity and a breakdown of ETH. By considering various types of disorder, we find that the functional forms of the distributions of matrix elements of the site-resolved magnetization operator mirror the distribution of the onsite disorder. We argue that this distribution is a direct consequence of the local observable having a finite overlap with moments of the Hamiltonian. We then demonstrate how to adjust the energy window when analyzing expectation values of local observables in disordered quantum many-body systems to correctly assess the system's adherence to ETH, and provide a link between the distribution of expectation values in eigenstates and the outcomes of quench experiments.

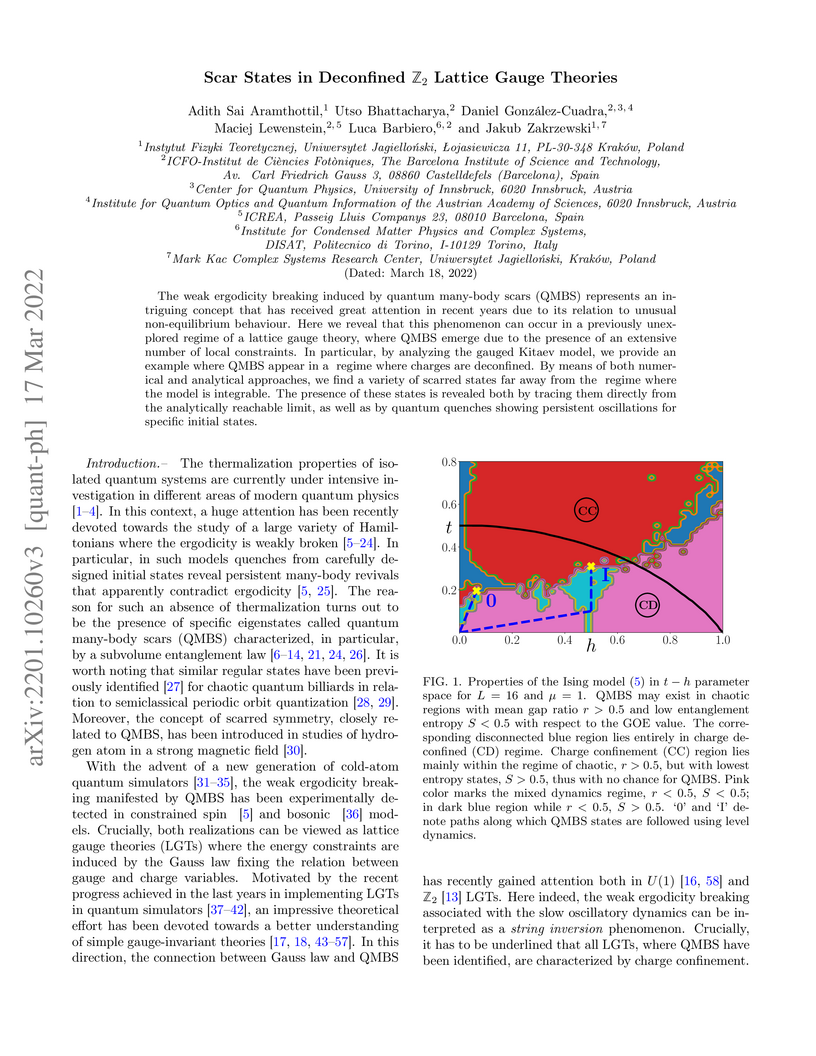
The weak ergodicity breaking induced by quantum many-body scars (QMBS) represents an intriguing concept that has received great attention in recent years due to its relation to unusual non-equilibrium behaviour. Here we reveal that this phenomenon can occur in a previously unexplored regime of a lattice gauge theory, where QMBS emerge due to the presence of an extensive number of local constraints. In particular, by analyzing the gauged Kitaev model, we provide an example where QMBS appear in a regime where charges are deconfined. By means of both numerical and analytical approaches, we find a variety of scarred states far away from the regime where the model is integrable. The presence of these states is revealed both by tracing them directly from the analytically reachable limit, as well as by quantum quenches showing persistent oscillations for specific initial states.

We present a thorough investigation of nonstabilizerness - a fundamental quantum resource that quantifies state complexity within the framework of quantum computing - in a one-dimensional U(1) lattice gauge theory. We show how nonstabilizerness is always extensive with volume, and has no direct relation to the presence of critical points. However, its derivatives typically display discontinuities across the latter: This indicates that nonstabilizerness is strongly sensitive to criticality, but in a manner that is very different from entanglement (that, typically, is maximal at the critical point). Our results indicate that error-corrected simulations of lattice gauge theories close to the continuum limit have similar computational costs to those at finite correlation length and provide rigorous lower bounds for quantum resources of such quantum computations.

We study many-body localization (MBL) transition in disordered Floquet systems using a polynomially filtered exact diagonalization (POLFED) algorithm. We focus on disordered kicked Ising model and quantitatively demonstrate that finite size effects at the MBL transition are less severe than in the random field XXZ spin chains widely studied in the context of MBL. Our conclusions extend also to other disordered Floquet models, indicating smaller finite size effects than those observed in the usually considered disordered autonomous spin chains. We observe consistent signatures of the transition to MBL phase for several indicators of ergodicity breaking in the kicked Ising model. Moreover, we show that an assumption of a power-law divergence of the correlation length at the MBL transition yields a critical exponent $\nu \approx 2$, consistent with the Harris criterion for 1D disordered systems.

Solutions of the wave equations for time-independent disordered media can exhibit Anderson localization where instead of wave propagation we observe their localization around different points in space. Photonic time crystals are spatially homogeneous media in which the refractive index changes periodically in time, leading to the formation of bands in the wave number domain. By analogy to Anderson localization in space, one might expect that the presence of temporal disorder in photonic time crystals would lead to Anderson localization in the time domain. Here, we show that indeed periodic modulations of the refractive index with the addition of temporal disorder lead to Anderson localization in time, where an electromagnetic field can emerge from the temporally modulated medium at a certain moment in time and then decay exponentially over time. Thus, we are dealing with a situation where, in a fluctuating three-dimensional medium, the birth and death of waves can occur, and the mechanism of this phenomenon corresponds to Anderson localization.

A measure of nonclassicality of quantum states based on the volume of the negative part of the Wigner function is proposed. We analyze this quantity for Fock states, squeezed displaced Fock states and cat-like states defined as coherent superposition of two Gaussian wave packets.

The quantum sun model is an interacting model that exhibits sharp signatures of ergodicity breaking phase transition. Here, we show that the model exhibits a many-body mobility edge. We provide analytical arguments for its existence, complemented by the state-of-the-art numerical simulations analysing gap ratios, Thouless times as well as entanglement entropy of eigenstates. We also introduce the quantum sun model with particle number conservation, and we argue that it shares many similarities with his unrestricted predecessor.

In analogy to spontaneous breaking of continuous space translation symmetry in the process of space crystal formation, it was proposed that spontaneous breaking of continuous time translation symmetry could lead to time crystal formation. In other words, a time-independent system prepared in the energy ground state is expected to reveal periodic motion under infinitely weak perturbation. In the case of the system proposed originally by Frank Wilczek, spontaneous breaking of time translation symmetry can not be observed if one starts with the ground state. We point out that the symmetry breaking can take place if the system is prepared in an excited eigenstate. The latter can be realized experimentally in ultra-cold atomic gases. We simulate the process of the spontaneous symmetry breaking due to measurements of particle positions and analyze the lifetime of the resulting symmetry broken state.

Rydberg tweezer arrays provide a platform for realizing spin-1/2 Hamiltonians with long-range tunnelings decaying according to power-law with the distance. We numerically investigate the effects of positional disorder and dimerization on the properties of excited states in such a one-dimensional system. Our model allows for the continuous tuning of dimerization patterns and disorder strength. We identify different distinct ergodicity-breaking regimes within the parameter space constrained by our geometry. Notably, one of these regimes exhibits a unique feature in which non-trivial symmetry-protected topological (SPT) properties of the ground state extend to a noticeable fraction of states across the entire spectrum. This interplay between localization and SPT makes the system particularly interesting, as localization should help with stabilization of topological excitations, while SPT states contribute to an additional delocalization. Other regions of parameters correspond to more standard nonergodic dynamics resembling many-body localization.

Thouless pumping enables the transport of particles in a one-dimensional periodic potential if the potential is slowly and periodically modulated in time. The change in the position of particles after each modulation period is quantized and depends solely on the topology of the pump cycle, making it robust against perturbations. Here, we demonstrate that Thouless pumping also allows for the realization of topologically protected quantized changes of the distance between atoms if the atomic s-wave scattering length is properly modulated in time.

This study delves into the efficacy of the Petz recovery map within the context of two paradigmatic quantum channels: dephasing and amplitude-damping. While prior investigations have predominantly focused on qubits, our research extends this inquiry to higher-dimensional systems. We introduce a novel, state-independent framework based on the Choi-Jamiołkowski isomorphism to evaluate the performance of the Petz map. By analyzing different channels and the (non-)unital nature of these processes, we emphasize the pivotal role of the reference state selection in determining the map's effectiveness. Furthermore, our analysis underscores the considerable impact of suboptimal choices on performance, prompting a broader consideration of factors such as system dimensionality.

Time crystalline structures can be created in periodically driven systems. They are temporal lattices which can reveal different condensed matter behaviours ranging from Anderson localization in time to temporal analogues of many-body localization or topological insulators. However, the potential practical applications of time crystalline structures have yet to be explored. Here, we pave the way for time-tronics where temporal lattices are like printed circuit boards for realization of a broad range of quantum devices. The elements of these devices can correspond to structures of dimensions higher than three and can be arbitrarily connected and reconfigured at any moment. Moreover, our approach allows for the construction of a quantum computer, enabling quantum gate operations for all possible pairs of qubits. Our findings indicate that the limitations faced in building devices using conventional spatial crystals can be overcome by adopting crystalline structures in time.

We report dynamical quantum phase transition portrait in the alternating field transverse XY spin chain with Dzyaloshinskii-Moriya interaction by investigating singularities in the Loschmidt echo and the corresponding rate function after a sudden quench of system parameters. Unlike the Ising model, the analysis of Loschmidt echo yields non-uniformly spaced transition times in this model. Comparative study between the equilibrium and the dynamical quantum phase transitions in this case reveals that there are quenches where one occurs without the other, and the regimes where they co-exist. However, such transitions happen only when quenching is performed across at least a single gapless or critical line. Contrary to equilibrium phase transitions, bipartite entanglement measures do not turn out to be useful for the detection, while multipartite entanglement emerges as a good identifier of this transition when the quench is done from a disordered phase of this model.

Level statistics of systems that undergo many--body localization transition are studied. An analysis of the gap ratio statistics from the perspective of inter- and intra-sample randomness allows us to pin point differences between transitions in random and quasi-random disorder, showing the effects due to Griffiths rare events for the former case. It is argued that the transition in the case of random disorder exhibits universal features that are identified by constructing an appropriate model of intermediate spectral statistics which is a generalization of the family of short-range plasma models. The considered weighted short-range plasma model yields a very good agreement both for level spacing distribution including its exponential tail and the number variance up to tens of level spacings outperforming previously proposed models. In particular, our model grasps the critical level statistics which arise at disorder strength for which the inter-sample fluctuations are the strongest. Going beyond the paradigmatic examples of many-body localization in spin systems, we show that the considered model also grasps the level statistics of disordered Bose- and Fermi-Hubbard models. The remaining deviations for long-range spectral correlations are discussed and attributed mainly to the intricacies of level unfolding.

The theory of Schwarzschild geodesics is revisited. Basing on a result by Weierstrass and Biermann, we derive a formula describing all non radial, timelike and null trajectories in terms of Weierstrass elliptic functions. Quite remarkably, a single formula works for an entire geodesic trajectory, even if it passes through turning points. Using this formula, we derive expressions for the proper and coordinate time along the geodesic.