discrete-mathematics
Snarls and superbubbles are fundamental pangenome decompositions capturing variant sites. These bubble-like structures underpin key tasks in computational pangenomics, including structural-variant genotyping, distance indexing, haplotype sampling, and variant annotation. Snarls can be quadratically-many in the size of the graph, and since their introduction in 2018 with the vg toolkit, there has been no work on identifying all snarls in linear time. Moreover, while it is known how to find superbubbles in linear time, this result is a highly specialized solution only achieved after a long series of papers.
We present the first algorithm identifying all snarls in linear time. This is based on a new representation of all snarls, of size linear in the input graph size, and which can be computed in linear time. Our algorithm is based on a unified framework that also provides a new linear-time algorithm for finding superbubbles. An observation behind our results is that all such structures are separated from the rest of the graph by two vertices (except for cases which are trivially computable), i.e. their endpoints are a 2-separator of the underlying undirected graph. Based on this, we employ the well-known SPQR tree decomposition, which encodes all 2-separators, to guide a traversal that finds the bubble-like structures efficiently.
We implemented our algorithms in C++ (available at this https URL) and evaluated them on various pangenomic datasets. Our algorithms outcompete or they are on the same level of existing methods. For snarls, we are up to two times faster than vg, while identifying all snarls. When computing superbubbles, we are up to 50 times faster than BubbleGun. Our SPQR tree framework provides a unifying perspective on bubble-like structures in pangenomics, together with a template for finding other bubble-like structures efficiently.
We study the problem of learning an unknown graph via group queries on node subsets, where each query reports whether at least one edge is present among the queried nodes. In general, learning arbitrary graphs with n nodes and k edges is hard in the non-adaptive setting, requiring Ω(min{k2logn,n2}) tests even when a small error probability is allowed. We focus on learning Erdős--Rényi (ER) graphs G∼\ER(n,q) in the non-adaptive setting, where the expected number of edges is kˉ=q(2n), and we aim to design an efficient testing--decoding scheme achieving asymptotically vanishing error probability. Prior work (Li--Fresacher--Scarlett, NeurIPS 2019) presents a testing--decoding scheme that attains an order-optimal number of tests O(kˉlogn) but incurs Ω(n2) decoding time, whereas their proposed sublinear-time algorithm incurs an extra (logkˉ)(logn) factor in the number of tests. We extend the binary splitting approach, recently developed for non-adaptive group testing, to the ER graph learning setting, and prove that the edge set can be recovered with high probability using O(kˉlogn) tests while attaining decoding time O(kˉ1+δlogn) for any fixed δ>0.
The concept of effective resistance, originally introduced in electrical circuit theory, has been extended to the setting of graphs by interpreting each edge as a resistor. In this context, the effective resistance between two vertices quantifies the total opposition to current flow when a unit current is injected at one vertex and extracted at the other. Beyond its physical interpretation, the effective resistance encodes rich structural and geometric information about the underlying graph: it defines a metric on the vertex set, relates to the topology of the graph through Foster's theorem, and determines the probability of an edge appearing in a random spanning tree. Generalizations of effective resistance to simplicial complexes have been proposed in several forms, often formulated as matrix products of standard operators associated with the complex.
In this paper, we present a twofold generalization of the effective resistance. First, we introduce a novel, basis-independent bilinear form, derived from an algebraic reinterpretation of circuit theory, that extends the classical effective resistance from graphs. Second, we extend this bilinear form to simplices, chains, and cochains within simplicial complexes. This framework subsumes and unifies all existing matrix-based formulations of effective resistance. Moreover, we establish higher-order analogues of several fundamental properties known in the graph case: (i) we prove that effective resistance induces a pseudometric on the space of chains and a metric on the space of cycles, and (ii) we provide a generalization of Foster's Theorem to simplicial complexes.
Researchers at the University of Oxford present a complete classification of long-refinement graphs where the maximum vertex degree is at most 4, thereby resolving previous gaps for specific graph sizes. The work also definitively proves the non-existence of "long-refinement pairs" for any graph order n ≥ 3, which were previously an open problem.
This paper provides a comprehensive complexity-theoretic analysis of counting linear regions in ReLU neural networks, formalizing six distinct definitions of these regions and demonstrating that most counting problems are computationally intractable. For shallow networks, counting is #P-complete, while for deep networks, even approximating the count is NP-hard, revealing fundamental limits on analyzing network expressiveness.
Job Shop Scheduling (JSS) is one of the most studied combinatorial
optimization problems. It involves scheduling a set of jobs with predefined
processing constraints on a set of machines to achieve a desired objective,
such as minimizing makespan, tardiness, or flowtime. Since it introduction, JSS
has become an attractive research area. Many approaches have been successfully
used to address this problem, including exact methods, heuristics, and
meta-heuristics. Furthermore, various learning-based approaches have been
proposed to solve the JSS problem. However, these approaches are still limited
when compared to the more established methods. This paper summarizes and
evaluates the most important works in the literature on machine learning
approaches for the JSSP. We present models, analyze their benefits and
limitations, and propose future research directions.
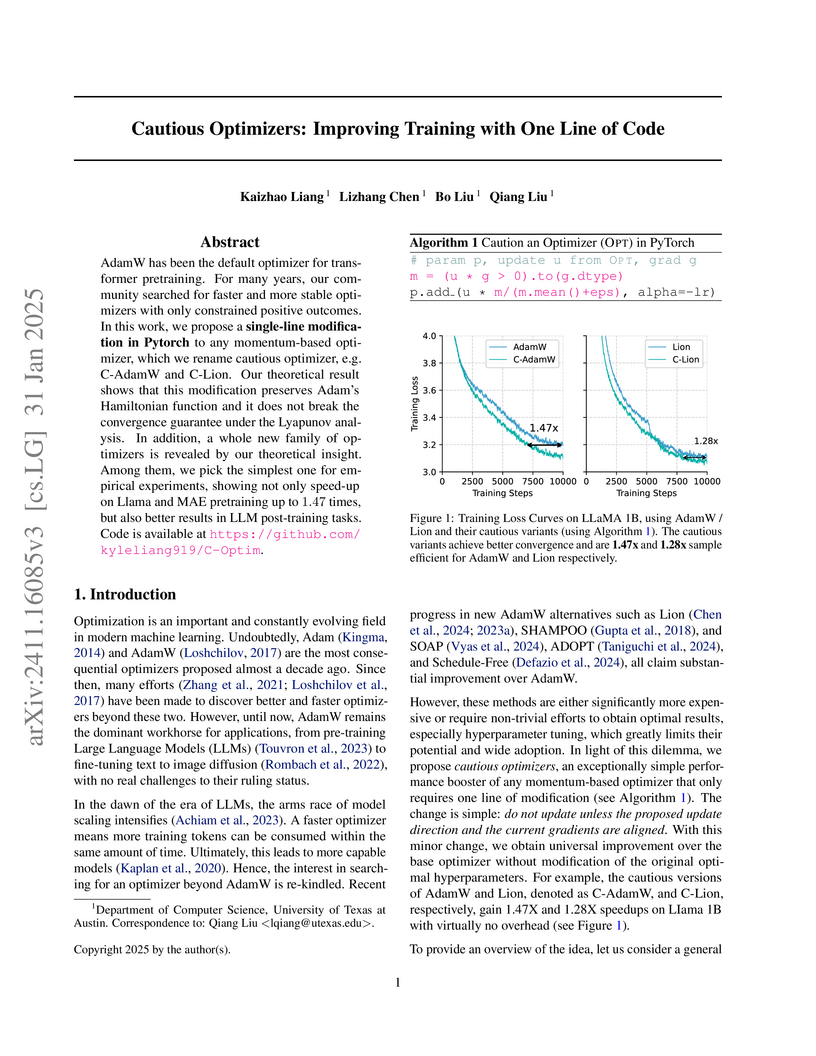
Researchers at the University of Texas at Austin developed 'Cautious Optimizers,' a method that introduces a one-line code modification to momentum-based optimizers to improve training efficiency and stability. This simple change, rooted in Hamiltonian dynamics, ensures parameter updates align with the current gradient, leading to up to 1.47 times faster training and improved downstream model quality across various deep learning tasks.
We consider the Cops and Robber pursuit-evasion game when the edge-set of the graph is allowed to change in time, possibly at every round. Specifically, the game is played on an infinite periodic sequence G=(G0,…,Gp−1)∗ of graphs on the same set V of n vertices: in round t, the topology of G is Gi=(V,Ei) where i≡t(modp).
Concentrating on the case of a single cop, we provide a characterization of copwin periodic temporal graphs, establishing several basic properties on their nature, and extending to the temporal domain classical C&R concepts such as covers and corners. Based on these results, we design an efficient algorithm for determining if a periodic temporal graph is copwin.
We also consider the case of k>1 cops. By shifting from a representation in terms of directed graphs to one in terms of directed multi-hypergraphs, we prove that all the fundamental properties established for k=1 continue to hold, providing a characterization of k-copwin periodic graphs, as well as a general strategy to determine if a periodic graph is k-copwin.
Our results do not rely on any assumption on properties such as connectivity, symmetry, reflexivity held by the individual graphs in the sequence. They are established for a unified version of the game that includes the standard games studied in the literature, both for undirected and directed graphs, and both when the players are fully active and when they are not. They hold also for a variety of settings not considered in the literature.
In this work we design graph neural network architectures that capture optimal approximation algorithms for a large class of combinatorial optimization problems, using powerful algorithmic tools from semidefinite programming (SDP). Concretely, we prove that polynomial-sized message-passing algorithms can represent the most powerful polynomial time algorithms for Max Constraint Satisfaction Problems assuming the Unique Games Conjecture. We leverage this result to construct efficient graph neural network architectures, OptGNN, that obtain high-quality approximate solutions on landmark combinatorial optimization problems such as Max-Cut, Min-Vertex-Cover, and Max-3-SAT. Our approach achieves strong empirical results across a wide range of real-world and synthetic datasets against solvers and neural baselines. Finally, we take advantage of OptGNN's ability to capture convex relaxations to design an algorithm for producing bounds on the optimal solution from the learned embeddings of OptGNN.
Learning to sample from intractable distributions over discrete sets without relying on corresponding training data is a central problem in a wide range of fields, including Combinatorial Optimization. Currently, popular deep learning-based approaches rely primarily on generative models that yield exact sample likelihoods. This work introduces a method that lifts this restriction and opens the possibility to employ highly expressive latent variable models like diffusion models. Our approach is conceptually based on a loss that upper bounds the reverse Kullback-Leibler divergence and evades the requirement of exact sample likelihoods. We experimentally validate our approach in data-free Combinatorial Optimization and demonstrate that our method achieves a new state-of-the-art on a wide range of benchmark problems.
Incorporating spectral information to enhance Graph Neural Networks (GNNs)
has shown promising results but raises a fundamental challenge due to the
inherent ambiguity of eigenvectors. Various architectures have been proposed to
address this ambiguity, referred to as spectral invariant architectures.
Notable examples include GNNs and Graph Transformers that use spectral
distances, spectral projection matrices, or other invariant spectral features.
However, the potential expressive power of these spectral invariant
architectures remains largely unclear. The goal of this work is to gain a deep
theoretical understanding of the expressive power obtainable when using
spectral features. We first introduce a unified message-passing framework for
designing spectral invariant GNNs, called Eigenspace Projection GNN (EPNN). A
comprehensive analysis shows that EPNN essentially unifies all prior spectral
invariant architectures, in that they are either strictly less expressive or
equivalent to EPNN. A fine-grained expressiveness hierarchy among different
architectures is also established. On the other hand, we prove that EPNN itself
is bounded by a recently proposed class of Subgraph GNNs, implying that all
these spectral invariant architectures are strictly less expressive than 3-WL.
Finally, we discuss whether using spectral features can gain additional
expressiveness when combined with more expressive GNNs.
Designing expressive Graph Neural Networks (GNNs) is a fundamental topic in the graph learning community. So far, GNN expressiveness has been primarily assessed via the Weisfeiler-Lehman (WL) hierarchy. However, such an expressivity measure has notable limitations: it is inherently coarse, qualitative, and may not well reflect practical requirements (e.g., the ability to encode substructures). In this paper, we introduce a unified framework for quantitatively studying the expressiveness of GNN architectures, addressing all the above limitations. Specifically, we identify a fundamental expressivity measure termed homomorphism expressivity, which quantifies the ability of GNN models to count graphs under homomorphism. Homomorphism expressivity offers a complete and practical assessment tool: the completeness enables direct expressivity comparisons between GNN models, while the practicality allows for understanding concrete GNN abilities such as subgraph counting. By examining four classes of prominent GNNs as case studies, we derive simple, unified, and elegant descriptions of their homomorphism expressivity for both invariant and equivariant settings. Our results provide novel insights into a series of previous work, unify the landscape of different subareas in the community, and settle several open questions. Empirically, extensive experiments on both synthetic and real-world tasks verify our theory, showing that the practical performance of GNN models aligns well with the proposed metric.
Directed acyclic graph (DAG) tasks are currently adopted in the real-time domain to model complex applications from the automotive, avionics, and industrial domains that implement their functionalities through chains of intercommunicating tasks. This paper studies the problem of scheduling real-time DAG tasks by presenting a novel schedulability test based on the concept of trivial schedulability. Using this schedulability test, we propose a new DAG scheduling framework (edge generation scheduling -- EGS) that attempts to minimize the DAG width by iteratively generating edges while guaranteeing the deadline constraint. We study how to efficiently solve the problem of generating edges by developing a deep reinforcement learning algorithm combined with a graph representation neural network to learn an efficient edge generation policy for EGS. We evaluate the effectiveness of the proposed algorithm by comparing it with state-of-the-art DAG scheduling heuristics and an optimal mixed-integer linear programming baseline. Experimental results show that the proposed algorithm outperforms the state-of-the-art by requiring fewer processors to schedule the same DAG tasks. The code is available at this https URL.
Researchers from MIT developed an efficient method to find globally optimal shortest paths in Graphs of Convex Sets (GCS), which involves selecting both a discrete path and continuous vertex positions. Their approach formulates the NP-hard problem as a strong and lightweight Mixed-Integer Convex Program (MICP) using perspective operators, achieving significantly faster solution times and tighter relaxations than prior methods for applications like optimal control of hybrid systems.
Mathematical proof aims to deliver confident conclusions, but a very similar
process of deduction can be used to make uncertain estimates that are open to
revision. A key ingredient in such reasoning is the use of a "default" estimate
of E[XY]=E[X]E[Y] in the absence of any
specific information about the correlation between X and Y, which we call
*the presumption of independence*. Reasoning based on this heuristic is
commonplace, intuitively compelling, and often quite successful -- but
completely informal.
In this paper we introduce the concept of a heuristic estimator as a
potential formalization of this type of defeasible reasoning. We introduce a
set of intuitively desirable coherence properties for heuristic estimators that
are not satisfied by any existing candidates. Then we present our main open
problem: is there a heuristic estimator that formalizes intuitively valid
applications of the presumption of independence without also accepting spurious
arguments?
The goal of this chapter is to review the main ideas that underlie the cavity method for disordered models defined on random graphs, as well as present some of its outcomes, focusing on the random constraint satisfaction problems for which it provided both a better understanding of the phase transitions they undergo, and suggestions for the development of algorithms to solve them.
In this paper, we study a class of discrete Morse functions, coming from Discrete Morse Theory, that are equivalent to a class of simplicial stacks, coming from Mathematical Morphology. We show that, as in Discrete Morse Theory, we can see the gradient vector field of a simplicial stack (seen as a discrete Morse function) as the only relevant information we should consider. Last, but not the least, we also show that the Minimum Spanning Forest of the dual graph of a simplicial stack is induced by the gradient vector field of the initial function. This result allows computing a watershed-cut from a gradient vector field.
A graph is a core or unretractive if all its endomorphisms are automorphisms. Well-known examples of cores include the Petersen graph and the graph of the dodecahedron -- both generalized Petersen graphs. We characterize the generalized Petersen graphs that are cores. A simple characterization of endomorphism-transitive generalized Petersen graphs follows. This extends the characterization of vertex-transitive generalized Petersen graphs due to Frucht, Graver, and Watkins and solves a problem of Fan and Xie.
Moreover, we study generalized Petersen graphs that are (underlying graphs of) Cayley graphs of monoids. We show that this is the case for the Petersen graph, answering a recent mathoverflow question, for the Desargues graphs, and for the dodecahedron -- answering a question of Knauer and Knauer. Moreover, we characterize the infinite family of generalized Petersen graphs that are Cayley graph of a monoid with generating connection set of size two. This extends Nedela and Škoviera's characterization of generalized Petersen graphs that are group Cayley graphs and complements results of Hao, Gao, and Luo.
Temporal graphs have been recently introduced to model changes to a given
network that occur throughout a fixed period of time. The Temporal Δ
Clique problem, that generalizes the well known Clique problem to temporal
graphs, has been studied in the context of finding nodes of interest in dynamic
networks [TCS '16]. We introduce the Temporal Δ Independent Set problem,
a temporal generalization of Independent Set. This problem is e.g. motivated in
the context of finding conflict-free schedules for maximum subsets of tasks,
that have certain (changing) constraints on each day they need to be performed.
We are specifically interested in the case where each task needs to be
performed in a certain time-interval on each day and two tasks are in conflict
on a certain day if their time-intervals on that day overlap. This leads us to
considering both problems on the restricted class of temporal unit interval
graphs, i.e., temporal graphs where each layer is a unit interval graph.
We present several hardness results as well as positive results. On the
algorithmic side, we provide constant-factor approximation algorithms for
instances of both problems where τ, the total number of time steps
(layers) of the temporal graph, and Δ, a parameter that allows us to
model conflict tolerance, are constants. We develop an exact FPT algorithm for
Temporal Δ Clique with respect to parameter τ+k. Finally, we use
the notion of order preservation for temporal unit interval graphs that,
informally, requires the intervals of every layer to obey a common ordering.
For both problems we provide an FPT algorithm parameterized by the size of
minimum vertex deletion set to order preservation.
We consider the sequential allocation of m balls (jobs) into n bins
(servers) by allowing each ball to choose from some bins sampled uniformly at
random. The goal is to maintain a small gap between the maximum load and the
average load. In this paper, we present a general framework that allows us to
analyze various allocation processes that slightly prefer allocating into
underloaded, as opposed to overloaded bins. Our analysis covers several natural
instances of processes, including:
The Caching process (a.k.a. memory protocol) as studied by Mitzenmacher,
Prabhakar and Shah (2002): At each round we only take one bin sample, but we
also have access to a cache in which the most recently used bin is stored. We
place the ball into the least loaded of the two.
The Packing process: At each round we only take one bin sample. If the load
is below some threshold (e.g., the average load), then we place as many balls
until the threshold is reached; otherwise, we place only one ball.
The Twinning process: At each round, we only take one bin sample. If the load
is below some threshold, then we place two balls; otherwise, we place only one
ball.
The Thinning process as recently studied by Feldheim and Gurel-Gurevich
(2021): At each round, we first take one bin sample. If its load is below some
threshold, we place one ball; otherwise, we place one ball into a
second bin sample.
As we demonstrate, our general framework implies for all these processes a
gap of O(logn) between the maximum load and average load, even
when an arbitrary number of balls m≥n are allocated (heavily loaded
case). Our analysis is inspired by a previous work of Peres, Talwar and Wieder
(2010) for the (1+β)-process, however here we rely on the interplay
between different potential functions to prove stabilization.
There are no more papers matching your filters at the moment.