In stochastic processes with absorbing states, the quasi-stationary distribution provides valuable insights into the long-term behaviour prior to absorption. In this work, we revisit two well-established numerical methods for its computation. The first is an iterative algorithm for solving the non-linear equation that defines the quasi-stationary distribution. We generalise this technique to accommodate general Markov stochastic processes, either with discrete or continuous state space, and with multiple absorbing states. The second is a Monte Carlo method with resetting, for which we propose a novel single-trajectory approach that uses the trajectory's own history to perform resets after absorption. In addition to these methodological contributions, we provide a detailed analysis of implementation aspects for both methods. We also compare their accuracy and efficiency across a range of examples. The results indicate that the iterative algorithm is generally the preferred choice for problems with simple boundaries, while the Monte Carlo approach is more suitable for problems with complex boundaries, where the implementation of the iterative algorithm is a challenging task.

We derive a general fluctuation theorem for quantum maps. The theorem applies to a broad class of quantum dynamics, such as unitary evolution, decoherence, thermalization, and other types of evolution for quantum open systems. The theorem reproduces well-known fluctuation theorems in a single and simplified framework and extends the Hatano-Sasa theorem to quantum nonequilibrium processes. Moreover, it helps to elucidate the physical nature of the environment inducing a given dynamics in an open quantum system.

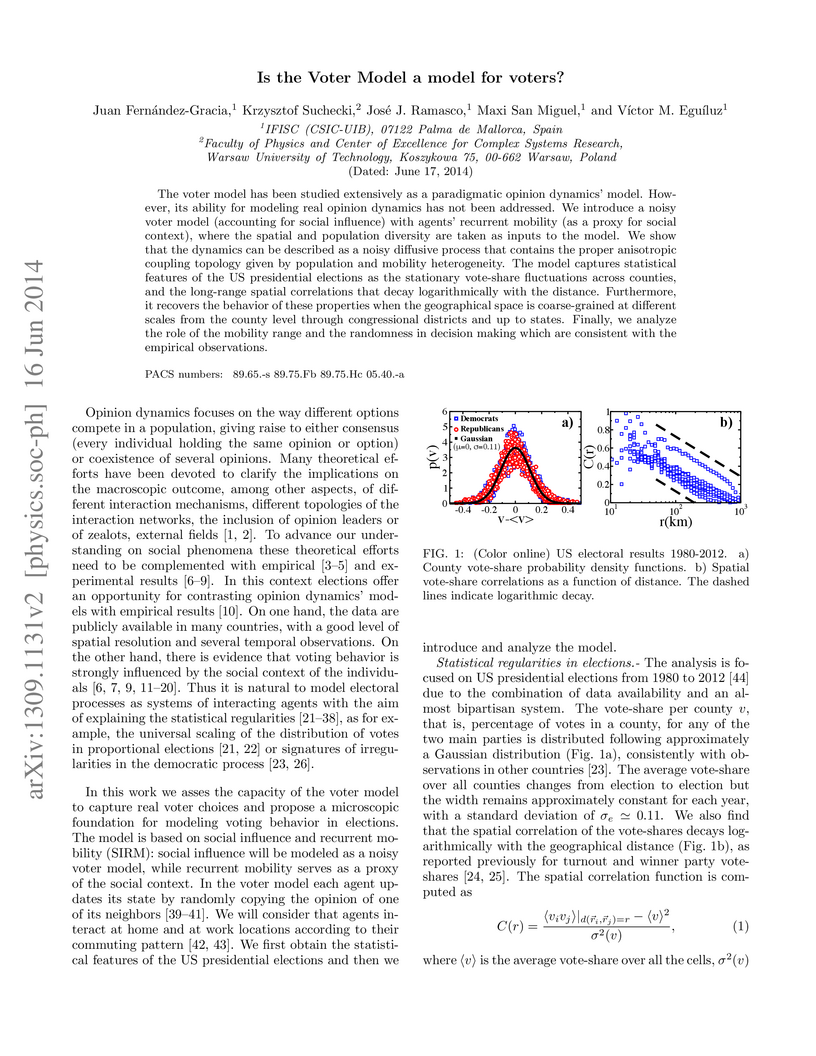
The voter model has been studied extensively as a paradigmatic opinion dynamics' model. However, its ability for modeling real opinion dynamics has not been addressed. We introduce a noisy voter model (accounting for social influence) with agents' recurrent mobility (as a proxy for social context), where the spatial and population diversity are taken as inputs to the model. We show that the dynamics can be described as a noisy diffusive process that contains the proper anysotropic coupling topology given by population and mobility heterogeneity. The model captures statistical features of the US presidential elections as the stationary vote-share fluctuations across counties, and the long-range spatial correlations that decay logarithmically with the distance. Furthermore, it recovers the behavior of these properties when a real-space renormalization is performed by coarse-graining the geographical scale from county level through congressional districts and up to states. Finally, we analyze the role of the mobility range and the randomness in decision making which are consistent with the empirical observations.

We determine the phase diagram of an Anderson impurity in contact with superconducting and normal-state leads for arbitrary ratio of the gap $\Delta$ to the Kondo temperature $T_K$. We observe a considerable effect of even very weak coupling to the normal lead that is usually considered as a non-perturbing tunneling probe. The numerical renormalization group results are analyzed in the context of relevant experimental scenarios such as parity crossing (doublet-singlet) quantum phase transitions induced by a gap reduction as well as novel Kondo features induced by the normal lead. We point out the important role of finite temperatures and magnetic fields. Overall, we find a very rich behavior of spectral functions with zero-bias anomalies which can emerge irrespective of whether the ground state is a doublet or a singlet. Our findings are pertinent to the tunnelling-spectroscopy experiments aiming at detecting Majorana modes in nanowires.

The exploitation of high volume of geolocalized data from social sport tracking applications of outdoor activities can be useful for natural resource planning and to understand the human mobility patterns during leisure activities. This geolocalized data represents the selection of hike activities according to subjective and objective factors such as personal goals, personal abilities, trail conditions or weather conditions. In our approach, human mobility patterns are analysed from trajectories which are generated by hikers. We propose the generation of the trail network identifying special points in the overlap of trajectories. Trail crossings and trailheads define our network and shape topological features. We analyse the trail network of Balearic Islands, as a case of study, using complex weighted network theory. The analysis is divided into the four seasons of the year to observe the impact of weather conditions on the network topology. The number of visited places does not decrease despite the large difference in the number of samples of the two seasons with larger and lower activity. It is in summer season where it is produced the most significant variation in the frequency and localization of activities from inland regions to coastal areas. Finally, we compare our model with other related studies where the network possesses a different purpose. One finding of our approach is the detection of regions with relevant importance where landscape interventions can be applied in function of the communities.

As global political preeminence gradually shifted from the United Kingdom to the United States, so did the capacity to culturally influence the rest of the world. In this work, we analyze how the world-wide varieties of written English are evolving. We study both the spatial and temporal variations of vocabulary and spelling of English using a large corpus of geolocated tweets and the Google Books datasets corresponding to books published in the US and the UK. The advantage of our approach is that we can address both standard written language (Google Books) and the more colloquial forms of microblogging messages (Twitter). We find that American English is the dominant form of English outside the UK and that its influence is felt even within the UK borders. Finally, we analyze how this trend has evolved over time and the impact that some cultural events have had in shaping it.

In stochastic processes with absorbing states, the quasi-stationary distribution provides valuable insights into the long-term behaviour prior to absorption. In this work, we revisit two well-established numerical methods for its computation. The first is an iterative algorithm for solving the non-linear equation that defines the quasi-stationary distribution. We generalise this technique to accommodate general Markov stochastic processes, either with discrete or continuous state space, and with multiple absorbing states. The second is a Monte Carlo method with resetting, for which we propose a novel single-trajectory approach that uses the trajectory's own history to perform resets after absorption. In addition to these methodological contributions, we provide a detailed analysis of implementation aspects for both methods. We also compare their accuracy and efficiency across a range of examples. The results indicate that the iterative algorithm is generally the preferred choice for problems with simple boundaries, while the Monte Carlo approach is more suitable for problems with complex boundaries, where the implementation of the iterative algorithm is a challenging task.

Elite football is believed to have evolved in recent years, but systematic evidence for the pace and form of that change is sparse. Drawing on event-level records for 13,067 matches in ten top-tier men's and women's leagues in England, Spain, Germany, Italy, and the United States (2020-2025), we quantify match dynamics with two views: conventional performance statistics and pitch-passing networks that track ball movement among a grid of pitch (field) regions. Between 2020 and 2025, average passing volume, pass accuracy, and the percent of passes made under pressure all rose. In general, the largest year-on-year changes occurred in women's competitions. Network measures offer alternative but complementary perspectives on the changing gameplay in recent years, normalized outreach in the pitch passing networks decreased, while the average shortest path lengths increased, indicating a wider ball circulation. Together, these indicators point to a sustained intensification of collective play across contemporary professional football.

A central concern of community ecology is the interdependence between interaction strengths and the underlying structure of the network upon which species interact. In this work we present a solvable example of such a feedback mechanism in a generalised Lotka-Volterra dynamical system. Beginning with a community of species interacting on a network with arbitrary degree distribution, we provide an analytical framework from which properties of the eventual `surviving community' can be derived. We find that highly-connected species are less likely to survive than their poorly connected counterparts, which skews the eventual degree distribution towards a preponderance of species with low degree, a pattern commonly observed in real ecosystems. Further, the average abundance of the neighbours of a species in the surviving community is lower than the community average (reminiscent of the famed friendship paradox). Finally, we show that correlations emerge between the connectivity of a species and its interactions with its neighbours. More precisely, we find that highly-connected species tend to benefit from their neighbours more than their neighbours benefit from them. These correlations are not present in the initial pool of species and are a result of the dynamics.

Trip distribution laws are basic for the travel demand characterization needed in transport and urban planning. Several approaches have been considered in the last years. One of them is the so-called gravity law, in which the number of trips is assumed to be related to the population at origin and destination and to decrease with the distance. The mathematical expression of this law resembles Newton's law of gravity, which explains its name. Another popular approach is inspired by the theory of intervening opportunities which argues that the distance has no effect on the destination choice, playing only the role of a surrogate for the number of intervening opportunities between them. In this paper, we perform a thorough comparison between these two approaches in their ability at estimating commuting flows by testing them against empirical trip data at different scales and coming from different countries. Different versions of the gravity and the intervening opportunities laws, including the recently proposed radiation law, are used to estimate the probability that an individual has to commute from one unit to another, called trip distribution law. Based on these probability distribution laws, the commuting networks are simulated with different trip distribution models. We show that the gravity law performs better than the intervening opportunities laws to estimate the commuting flows, to preserve the structure of the network and to fit the commuting distance distribution although it fails at predicting commuting flows at large distances. Finally, we show that the different approaches can be used in the absence of detailed data for calibration since their only parameter depends only on the scale of the geographic unit.

Most existing results in the analysis of quantum reservoir computing (QRC) systems with classical inputs have been obtained using the density matrix formalism. This paper shows that alternative representations can provide better insights when dealing with design and assessment questions. More explicitly, system isomorphisms are established that unify the density matrix approach to QRC with the representation in the space of observables using Bloch vectors associated with Gell-Mann bases. It is shown that these vector representations yield state-affine systems (SAS) previously introduced in the classical reservoir computing literature and for which numerous theoretical results have been established. This connection is used to show that various statements in relation to the fading memory (FMP) and the echo state (ESP) properties are independent of the representation, and also to shed some light on fundamental questions in QRC theory in finite dimensions. In particular, a necessary and sufficient condition for the ESP and FMP to hold is formulated using standard hypotheses, and contractive quantum channels that have exclusively trivial semi-infinite solutions are characterized in terms of the existence of input-independent fixed points.

In the analysis of complex ecosystems it is common to use random interaction coefficients, often assumed to be such that all species are statistically equivalent. In this work we relax this assumption by choosing interactions according to the cascade model, which we incorporate into a generalised Lotka-Volterra dynamical system. These interactions impose a hierarchy in the community. Species benefit more, on average, from interactions with species further below them in the hierarchy than from interactions with those above. Using dynamic mean-field theory, we demonstrate that a strong hierarchical structure is stabilising, but that it reduces the number of species in the surviving community, as well as their abundances. Additionally, we show that increased heterogeneity in the variances of the interaction coefficients across positions in the hierarchy is destabilising. We also comment on the structure of the surviving community and demonstrate that the abundance and probability of survival of a species is dependent on its position in the hierarchy.

In 2002, in a seminal article, Christoph Bandt and Bernd Pompe proposed a new methodology for the analysis of complex time series, now known as Ordinal Analysis. The ordinal methodology is based on the computation of symbols (known as ordinal patterns) which are defined in terms of the temporal ordering of data points in a time series, and whose probabilities are known as ordinal probabilities. With the ordinal probabilities, the Shannon entropy can be calculated, which is the permutation entropy. Since it was proposed, the ordinal method has found applications in fields as diverse as biomedicine and climatology. However, some properties of ordinal probabilities are still not fully understood, and how to combine the ordinal approach of feature extraction with machine learning techniques for model identification, time series classification or forecasting remains a challenge. The objective of this perspective article is to present some recent advances and to discuss some open problems.

We analyze solutions to the stochastic skeleton model, a minimal nonlinear oscillator model for the Madden-Julian Oscillation (MJO). This model has been recognized for its ability to reproduce several large-scale features of the MJO. In previous studies, the model's forcings were predominantly chosen to be mathematically simple and time-independent. Here, we present solutions to the model with time-dependent observation-based forcing functions. Our results show that the model, with these more realistic forcing functions, successfully replicates key characteristics of MJO events, such as their lifetime, extent, and amplitude, whose statistics agree well with observations. However, we find that the seasonality of MJO events and the spatial variations in the MJO properties are not well reproduced. Having implemented the model in the presence of time-dependent forcings, we can analyze the impact of temporal variability at different time scales. In particular, we study the model's ability to reflect changes in MJO characteristics under the different phases of ENSO. We find that it does not capture differences in studied characteristics of MJO events in response to differences in conditions during El Ni\~no, La Ni\~na, and neutral ENSO.

Revealing the structural properties and understanding the evolutionary mechanisms of the urban heavy truck mobility network (UHTMN) provide insights in assessment of freight policies to manage and regulate the urban freight system, and are of vital importance for improving the livability and sustainability of cities. Although massive urban heavy truck mobility data become available in recent years, in-depth studies on the structure and evolution of UHTMN are still lacking. Here we use massive urban heavy truck GPS data in China to construct the UHTMN and reveal its a wide range of structure properties. We further develop an evolving network model that simultaneously considers weight, space and system element duplication. Our model reproduces the observed structure properties of UHTMN and helps us understand its underlying evolutionary mechanisms. Our model also provides new perspectives for modeling the evolution of many other real-world networks, such as protein interaction networks, citation networks and air transportation networks.

We address the structure of the Liouvillian superoperator for a broad class of bosonic and fermionic Markovian open systems interacting with stationary environments. We show that the accurate application of the partial secular approximation in the derivation of the Bloch-Redfield master equation naturally induces a symmetry on the superoperator level, which may greatly reduce the complexity of the master equation by decomposing the Liouvillian superoperator into independent blocks. Moreover, we prove that, if the steady state of the system is unique, one single block contains all the information about it, and that this imposes a constraint on the possible steady-state coherences of the unique state, ruling out some of them. To provide some examples, we show how the symmetry appears for two coupled spins interacting with separate baths, as well as for two harmonic oscillators immersed in a common environment. In both cases the standard derivation and solution of the master equation is simplified, as well as the search for the steady state. The block-diagonalization does not appear when a local master equation is chosen.

Eastern Boundary Upwelling Systems (EBUS) are characterized by a high productivity of plankton associated with large commercial fisheries, thus playing key biological and socio-economical roles. The aim of this work is to make a comparative study of these four upwelling systems focussing on their surface stirring, using the Finite Size Lyapunov Exponents (FSLEs), and their biological activity, based on satellite data. First, the spatial distribution of horizontal mixing is analysed from time averages and from probability density functions of FSLEs. Then we studied the temporal variability of surface stirring focussing on the annual and seasonal cycle. There is a global negative correlation between surface horizontal mixing and chlorophyll standing stocks over the four areas. To try to better understand this inverse relationship, we consider the vertical dimension by looking at the Ekman-transport and vertical velocities. We suggest the possibility of a changing response of the phytoplankton to sub/mesoscale turbulence, from a negative effect in the very productive coastal areas to a positive one in the open ocean.

Squeezing is known to be a quantum resource in many applications in metrology, cryptography, and computing, being related to entanglement in multimode settings. In this work, we address the effects of squeezing in neuromorphic machine learning for time series processing. In particular, we consider a loop-based photonic architecture for reservoir computing and address the effect of squeezing in the reservoir, considering a Hamiltonian with both active and passive coupling terms. Interestingly, squeezing can be either detrimental or beneficial for quantum reservoir computing when moving from ideal to realistic models, accounting for experimental noise. We demonstrate that multimode squeezing enhances its accessible memory, which improves the performance in several benchmark temporal tasks. The origin of this improvement is traced back to the robustness of the reservoir to readout noise as squeezing increases.

Why are living systems complex? Why does the biosphere contain living beings with complexity features beyond those of the simplest replicators? What kind of evolutionary pressures result in more complex life forms? These are key questions that pervade the problem of how complexity arises in evolution. One particular way of tackling this is grounded in an algorithmic description of life: living organisms can be seen as systems that extract and process information from their surroundings in order to reduce uncertainty. Here we take this computational approach using a simple bit string model of coevolving agents and their parasites. While agents try to predict their worlds, parasites do the same with their hosts. The result of this process is that, in order to escape their parasites, the host agents expand their computational complexity despite the cost of maintaining it. This, in turn, is followed by increasingly complex parasitic counterparts. Such arms races display several qualitative phases, from monotonous to punctuated evolution or even ecological collapse. Our minimal model illustrates the relevance of parasites in providing an active mechanism for expanding living complexity beyond simple replicators, suggesting that parasitic agents are likely to be a major evolutionary driver for biological complexity.