Soldier crabs Mictyris guinotae exhibit pronounced swarming behaviour. The swarms of the crabs tolerant of perturbations. In computer models and laboratory experiments we demonstrate that swarms of soldier crabs can implement logical gates when placed in a geometrically constrained environment.

We report a new system of artificial life called Lenia (from Latin lenis "smooth"), a two-dimensional cellular automaton with continuous space-time-state and generalized local rule. Computer simulations show that Lenia supports a great diversity of complex autonomous patterns or "lifeforms" bearing resemblance to real-world microscopic organisms. More than 400 species in 18 families have been identified, many discovered via interactive evolutionary computation. They differ from other cellular automata patterns in being geometric, metameric, fuzzy, resilient, adaptive, and rule-generic. We present basic observations of the system regarding the properties of space-time and basic settings. We provide a broad survey of the lifeforms, categorize them into a hierarchical taxonomy, and map their distribution in the parameter hyperspace. We describe their morphological structures and behavioral dynamics, propose possible mechanisms of their self-propulsion, self-organization and plasticity. Finally, we discuss how the study of Lenia would be related to biology, artificial life, and artificial intelligence.

When involution affects individuals, their efforts do not augment resources but merely compete for limited resources. From entrance exams to company overtime, such efforts lead to unnecessary costs, undermining group welfare. Meanwhile, the individual advantages or collective disadvantages from this unnecessary effort may accumulate over time, such as the long-term validity of test scores. To identify the role of this memory factor, we propose a memory-based involution game model. In a more competitive environment, our findings suggest: (i) with scant social resources, increasing memory length curbs involution, (ii) with moderate resources, increasing memory length initially intensifies involution but later reduces it, and (iii) with abundant social resources, increasing memory length amplifies involution. Conversely, in a less competitive environment, involution consistently decreases with a larger memory length. Our research provides insights into mitigating involution by considering memory effects.

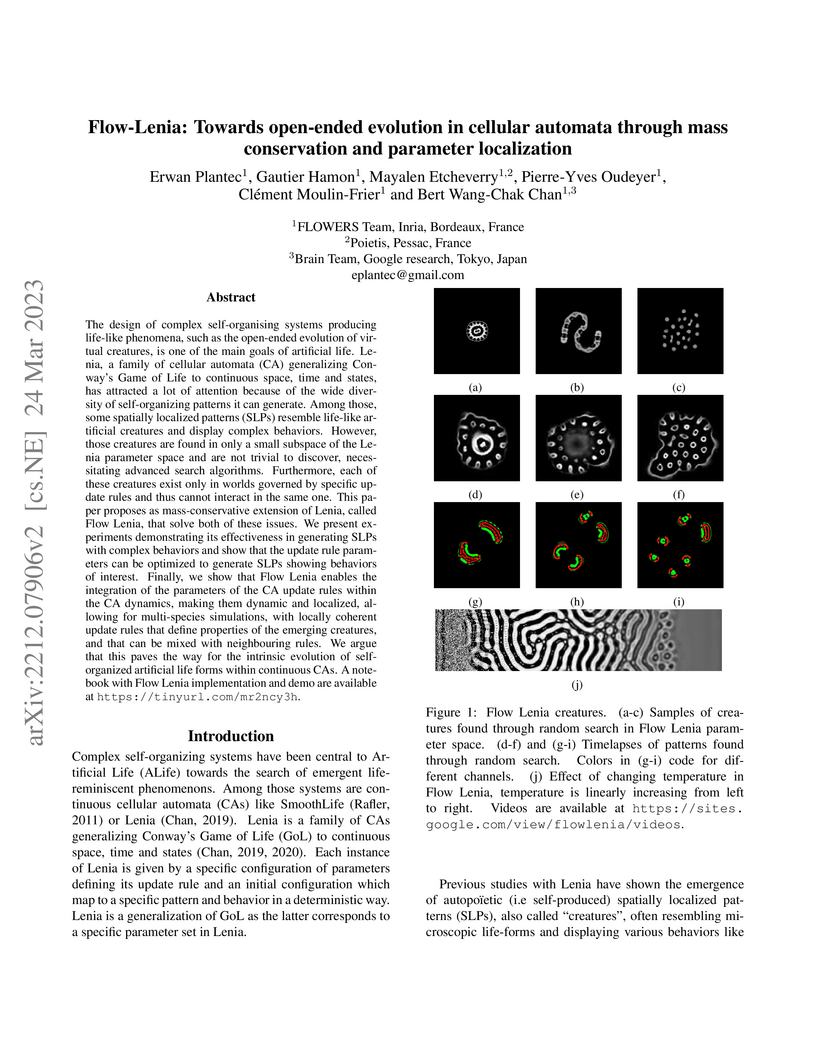
The design of complex self-organising systems producing life-like phenomena, such as the open-ended evolution of virtual creatures, is one of the main goals of artificial life. Lenia, a family of cellular automata (CA) generalizing Conway's Game of Life to continuous space, time and states, has attracted a lot of attention because of the wide diversity of self-organizing patterns it can generate. Among those, some spatially localized patterns (SLPs) resemble life-like artificial creatures and display complex behaviors. However, those creatures are found in only a small subspace of the Lenia parameter space and are not trivial to discover, necessitating advanced search algorithms. Furthermore, each of these creatures exist only in worlds governed by specific update rules and thus cannot interact in the same one. This paper proposes as mass-conservative extension of Lenia, called Flow Lenia, that solve both of these issues. We present experiments demonstrating its effectiveness in generating SLPs with complex behaviors and show that the update rule parameters can be optimized to generate SLPs showing behaviors of interest. Finally, we show that Flow Lenia enables the integration of the parameters of the CA update rules within the CA dynamics, making them dynamic and localized, allowing for multi-species simulations, with locally coherent update rules that define properties of the emerging creatures, and that can be mixed with neighbouring rules. We argue that this paves the way for the intrinsic evolution of self-organized artificial life forms within continuous CAs.

Symmetry resolved entanglement and entanglement asymmetry are two measures of quantum correlations sensitive to symmetries of the system. Here we discuss their non-equilibrium dynamics in the Rule 54 cellular automaton, a simple, yet interacting, integrable model. Both quantities can be expressed in terms of the more analytically tractable "charged moments", i.e. traces of powers of a suitably deformed density matrix, via a replica trick. We express them in terms of a tensor network, which we contract in space using a system of local algebraic relations. This gives the asymptotic form for the charged moments, valid in the regime of large but finite time that is shorter than all the relevant subsystem sizes. In this regime the charge moments decay exponentially with the rate given by the leading solution to a cubic equation.

To identify potential universal cellular automata, a method is developed to measure information processing capacity of elementary cellular automata. We consider two features of cellular automata: Ability to store information, and ability to process information. We define local collections of cells as particles of cellular automata and consider information contained by particles. By using this method, information channels and channels' intersections can be shown. By observing these two features, potential universal cellular automata are classified into a certain class, and all elementary cellular automata can be classified into four groups, which correspond to S. Wolfram's four classes: 1) Homogeneous; 2) Regular; 3) Chaotic and 4) Complex. This result shows that using abilities of store and processing information to characterize complex systems is effective and succinct. And it is found that these abilities are capable of quantifying the complexity of systems.

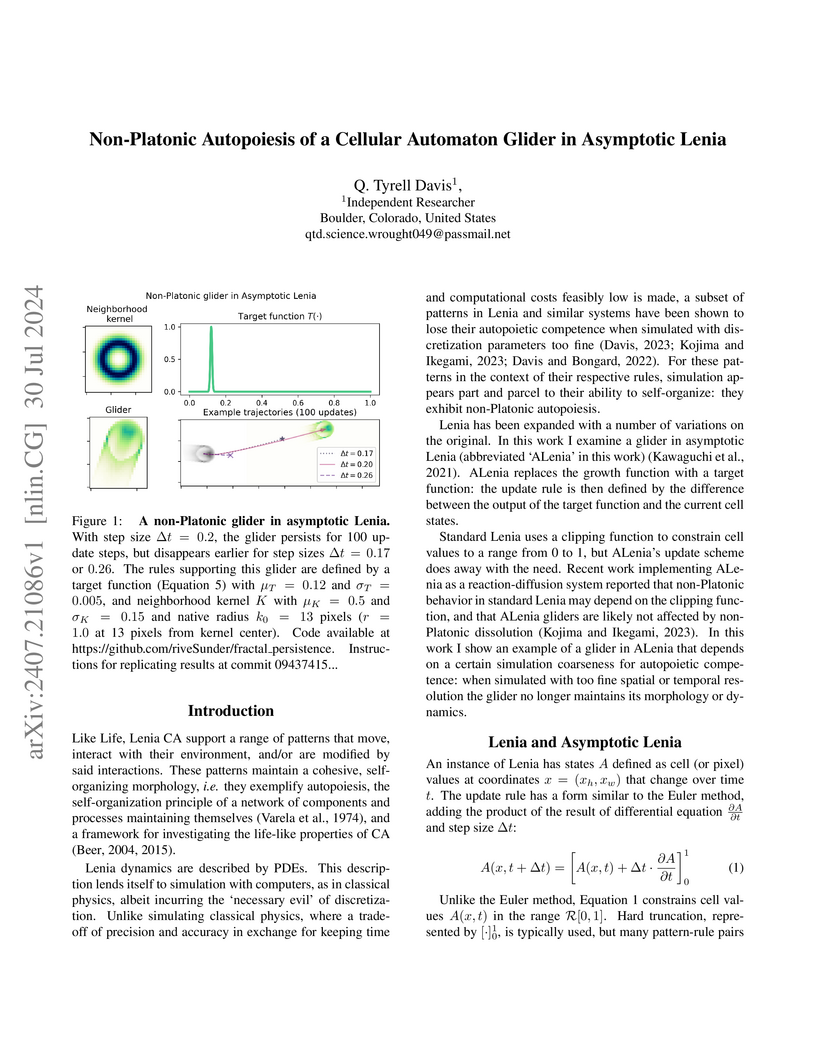
Like Life, Lenia CA support a range of patterns that move, interact with their environment, and/or are modified by said interactions. These patterns maintain a cohesive, self-organizing morphology, i.e. they exemplify autopoiesis, the self-organization principle of a network of components and processes maintaining themselves. Recent work implementing Asymptotic Lenia as a reaction-diffusion system reported that non-Platonic behavior in standard Lenia may depend on the clipping function, and that ALenia gliders are likely not subject to non-Platonic instability. In this work I show an example of a glider in ALenia that depends on a certain simulation coarseness for autopoietic competence: when simulated with too fine spatial or temporal resolution the glider no longer maintains its morphology or dynamics. I also show that instability maps of the asymptotic Lenia glider, and others in different CA framworks, show fractal retention of fine boundary detail down to the limit of floating point precision.

In reaction-diffusion models of annihilation reactions in low dimensions, single-particle dynamics provides a bottleneck for reactions, leading to an anomalously slow approach to the empty state. Here, we construct a reaction model with a reciprocal bottleneck on particle dynamics where single-particle motion conserves the center of mass. We show that such a constrained reaction-diffusion dynamics does not approach an empty state but freezes at late times in a state with fragmented particle clusters, and that the late-time dynamics and asymptotic density are universal. Our setup thus constitutes a minimal model for the fragmentation of a one-dimensional lattice into independent particle clusters, and we provide exact results for the final density in the large-reaction rate limit. We suggest that the universal reaction dynamics could be observable in experiments with cold atoms or in the Auger recombination of exciton gases.

Early warning indicators often suffer from the shortness and coarse-graining of real-world time series. Furthermore, the typically strong and correlated noise contributions in real applications are severe drawbacks for statistical measures. Even under favourable simulation conditions the measures are of limited capacity due to their qualitative nature and sometimes ambiguous trend-to-noise ratio. In order to solve these shortcomings, we analyse the stability of the system via the slope of the deterministic term of a Langevin equation, which is hypothesized to underlie the system dynamics close to the fixed point. The open-source available method is applied to a previously studied seasonal ecological model under noise levels and correlation scenarios commonly observed in real world data. We compare the results to autocorrelation, standard deviation, skewness and kurtosis as leading indicator candidates by a Bayesian model comparison with a linear and a constant model. We show that the slope of the deterministic term is a promising alternative due to its quantitative nature and high robustness against noise levels and types. The commonly computed indicators apart from the autocorrelation with deseasonalization fail to provide reliable insights into the stability of the system in contrast to a previously performed study in which the standard deviation was found to perform best. In addition, we discuss the significant influence of the seasonal nature of the data to the robust computation of the various indicators, before we determine approximately the minimal amount of data per time window that leads to significant trends for the drift slope estimations.

We consider the effect of noise in sparse Boolean Networks with redundant functions. We show that they always exhibit a non-zero error level, and the dynamics undergoes a phase transition from non-ergodicity to ergodicity, as a function of noise, after which the system is no longer capable of preserving a memory if its initial state. We obtain upper-bounds on the critical value of noise for networks of different sparsity.

Why are living systems complex? Why does the biosphere contain living beings with complexity features beyond those of the simplest replicators? What kind of evolutionary pressures result in more complex life forms? These are key questions that pervade the problem of how complexity arises in evolution. One particular way of tackling this is grounded in an algorithmic description of life: living organisms can be seen as systems that extract and process information from their surroundings in order to reduce uncertainty. Here we take this computational approach using a simple bit string model of coevolving agents and their parasites. While agents try to predict their worlds, parasites do the same with their hosts. The result of this process is that, in order to escape their parasites, the host agents expand their computational complexity despite the cost of maintaining it. This, in turn, is followed by increasingly complex parasitic counterparts. Such arms races display several qualitative phases, from monotonous to punctuated evolution or even ecological collapse. Our minimal model illustrates the relevance of parasites in providing an active mechanism for expanding living complexity beyond simple replicators, suggesting that parasitic agents are likely to be a major evolutionary driver for biological complexity.

The cellular automaton is a widely known model of both reversible and irreversible computations. The family of reversible second-order cellular automata considered in this work is appropriate both for construction of logic gates and analysis of damage distribution. The quantities such as formal dimension of damage patterns can be used only for rough estimation of consequences of particular faults and numerical experiments are provided for illustration of some subtleties. Such analysis demonstrates high sensitivity to errors from defects, lack of synchronization and too short intervals between signals.

Elementary cellular automata deterministically map a binary sequence to another using simple local rules. Visualizing the structure of this mapping is difficult because the number of nodes (i.e. possible binary sequences) grows exponentially. If periodic boundary conditions are used, rotation of a sequence and rule application to that sequence commute. This allows us to recover the rotational invariance property of loops and to reduce the number of nodes by only considering binary necklaces, the equivalence class of n-character strings taking all rotations as equivalent. Combining together many equivalent histories reveals the general structure of the rule, both visually and computationally. In this work, we investigate the structure of necklace-networks induced by the 256 Elementary Cellular Automata rules and show how their network structure change as the length of necklaces grow.

The year of 2024 marks the 25th anniversary of the publication of evoloops, an evolutionary variant of Chris Langton's self-reproducing loops which proved constructively that Darwinian evolution of self-reproducing organisms by variation and natural selection is possible within deterministic cellular automata. Over the last few decades, this line of Artificial Life research has since undergone several important developments. Although it experienced a relative dormancy of activities for a while, the recent rise of interest in open-ended evolution and the success of continuous cellular automata models have brought researchers' attention back to how to make spatio-temporal patterns self-reproduce and evolve within spatially distributed computational media. This article provides a review of the relevant literature on this topic over the past 25 years and highlights the major accomplishments made so far, the challenges being faced, and promising future research directions.

We propose a four-way classification of two-dimensional semi-totalistic cellular automata that is different than Wolfram's, based on two questions with yes-or-no answers: do there exist patterns that eventually escape any finite bounding box placed around them? And do there exist patterns that die out completely? If both of these conditions are true, then a cellular automaton rule is likely to support spaceships, small patterns that move and that form the building blocks of many of the more complex patterns that are known for Life. If one or both of these conditions is not true, then there may still be phenomena of interest supported by the given cellular automaton rule, but we will have to look harder for them. Although our classification is very crude, we argue that it is more objective than Wolfram's (due to the greater ease of determining a rigorous answer to these questions), more predictive (as we can classify large groups of rules without observing them individually), and more accurate in focusing attention on rules likely to support patterns with complex behavior. We support these assertions by surveying a number of known cellular automaton rules.

We present what we argue is the generic generalization of Conway's "Game of Life" to a continuous domain. We describe the theoretical model and the explicit implementation on a computer.

We present a method to solve initial and boundary value problems using artificial neural networks. A trial solution of the differential equation is written as a sum of two parts. The first part satisfies the boundary (or initial) conditions and contains no adjustable parameters. The second part is constructed so as not to affect the boundary conditions. This part involves a feedforward neural network, containing adjustable parameters (the weights). Hence by construction the boundary conditions are satisfied and the network is trained to satisfy the differential equation. The applicability of this approach ranges from single ODE's, to systems of coupled ODE's and also to PDE's. In this article we illustrate the method by solving a variety of model problems and present comparisons with finite elements for several cases of partial differential equations.

Between the years 2020 to 2022, the world was hit by the pandemic of COVID-19 giving rise to an extremely grave situation. The global economy was badly hurt due to the consequences of various intervention strategies (like social distancing, lockdown) which were applied by different countries to control this pandemic. There are multiple speculations that humanity will again face such pandemics in the future. Thus it is very important to learn and gain knowledge about the spread of such infectious diseases and the various factors which are responsible for it. In this study, we have extended our previous work (Chowdhury this http URL., 2022) on the probabilistic cellular automata (CA) model to reproduce the spread of COVID-19 in several countries by modifying its earlier used neighbourhood criteria. This modification gives us the liberty to adopt the effect of different restrictions like lockdown and social distancing in our model. We have done some theoretical analysis for initial infection and simulations to gain insights into our model. We have also studied the data from eight countries for COVID-19 in a window of 876 days and compared it with our model. We have developed a proper framework to fit our model on the data for confirmed cases of COVID-19 and have also re-checked the goodness of the fit with the data of the deceased cases for this pandemic. This model fits well with different peaks of COVID-19 data for all the eight countries and can be possibly generalized for a global prediction.

We describe software that searches for spaceships in Conway's Game of Life and related two-dimensional cellular automata. Our program searches through a state space related to the de Bruijn graph of the automaton, using a method that combines features of breadth first and iterative deepening search, and includes fast bit-parallel graph reachability and path enumeration algorithms for finding the successors of each state. Successful results include a new 2c/7 spaceship in Life, found by searching a space with 2^126 states.