We investigate the behaviour of elliptic Feynman integrals under modular transformations. This has a practical motivation: Through a suitable modular transformation we can achieve that the nome squared is a small quantity, leading to fast numerical evaluations. Contrary to the case of multiple polylogarithms, where it is sufficient to consider just variable transformations for the numerical evaluations of multiple polylogarithms, it is more natural in the elliptic case to consider a combination of a variable transformation (i.e. a modular transformation) together with a redefinition of the master integrals. Thus we combine a coordinate transformation on the base manifold with a basis transformation in the fibre. Only in the combination of the two transformations we stay within the same class of functions.

We show that optically encoded two-qubit Bell states can be unambiguously discriminated with a success probability of more than 50% in both single-rail and dual-rail encodings by using active linear-optical resources that include Gaussian squeezing operations. These results are in contrast to the well-known upper bound of 50% for unambiguous discrimination of dual-rail Bell states using passive, static linear optics and arbitrarily many vacuum modes. We present experimentally feasible schemes that improve the success probability to 64.3% in dual-rail and to 62.5% in single-rail for a uniform random distribution of Bell states. Conceptually, this demonstrates that neither interactions that induce nonlinear mode transformations (such as Kerr interactions) nor auxiliary entangled photons are required to go beyond the one-half limit. We discuss the optimality of our single-rail scheme, and talk about an application of our dual-rail scheme in quantum communication.

Quantum error correction codes based on continuous variables play an important role for the implementation of quantum communication systems. A natural application of such codes occurs within quantum repeater systems which are used to combat severe channel losses and local gate errors. In particular, channel loss drastically reduces the distance of communication between remote users. Here we consider a cavity-QED based repeater scheme to address the losses in the quantum channel. This repeater scheme relies on the transmission of a specific class of rotationally invariant error-correcting codes. We compare several rotation-symmetric bosonic codes (RSBCs) being used to encode the initial states of two remote users connected by a quantum repeater network against the convention of the cat codes and we quantify the performance of the system using the secret key rate. In particular, we determine the number of stations required to exchange a secret key over a fixed distance and establish the resource overhead.

We introduce tile codes, a simple yet powerful way of constructing quantum codes that are local on a planar 2D-lattice. Tile codes generalize the usual surface code by allowing for a bit more flexibility in terms of locality and stabilizer weight. Our construction does not compromise on the fact that the codes are local on a lattice with open boundary conditions. Despite its simplicity, we use our construction to find codes with parameters $[[288, 8, 12]]$using weight-6 stabilizers and$[[288, 8, 14]]$ using weight-8 stabilizers, outperforming all previously known constructions in this direction. Allowing for a slightly higher non-locality, we find a $[[512, 18, 19]]$ code using weight-8 stabilizers, which outperforms the rotated surface code by a factor of more than 12. Our approach provides a unified framework for understanding the structure of codes that are local on a 2D planar lattice and offers a systematic way to explore the space of possible code parameters. In particular, due to its simplicity, the construction naturally accommodates various types of boundary conditions and stabilizer configurations, making it a versatile tool for quantum error correction code design.

We report on three improvements in the context of Feynman integral reduction and $\varepsilon$-factorised differential equations: Firstly, we show that with a specific choice of prefactors, we trivialise the $\varepsilon$-dependence of the integration-by-parts identities. Secondly, we observe that with a specific choice of order relation in the Laporta algorithm, we directly obtain a basis of master integrals, whose differential equation on the maximal cut is in Laurent polynomial form with respect to $\varepsilon$ and compatible with a particular filtration. Thirdly, we prove that such a differential equation can always be transformed to an $\varepsilon$-factorised form. This provides a systematic algorithm to obtain an $\varepsilon$-factorised differential equation for any Feynman integral. Furthermore, the choices for the prefactors and the order relation significantly improve the efficiency of the reduction algorithm.

As the study of active matter has developed into one of the most rapidly growing subfields of condensed matter physics, more and more kinds of physical systems have been included in this framework. While the word 'active' is often thought of as referring to self-propelled particles, it is also applied to a large variety of other systems such as non-polar active nematics or certain particles with non-reciprocal interactions. Developing novel forms of active matter, as attempted, e.g., in the framework of quantum active matter, requires a clear idea of what active matter is. Here, we critically discuss how the understanding of active matter has changed over time, what precisely a definition of 'active matter' can look like, and to what extent it is (still) possible to define active matter in a way that covers all systems that are commonly understood as active matter while distinguishing them from other driven systems. Moreover, we discuss the definition of an 'active field theory', where 'active' is used as an attribute of a theoretical model rather than of a physical system. We show that the usage of the term 'active' requires agreement on a coarse-grained viewpoint. We discuss the meaning of 'active' both in general terms and via the specific examples of chemically driven particles, ultrasound-driven particles, active nematics, particles with non-reciprocal interactions, intracellular phase separation, and quantum active matter.

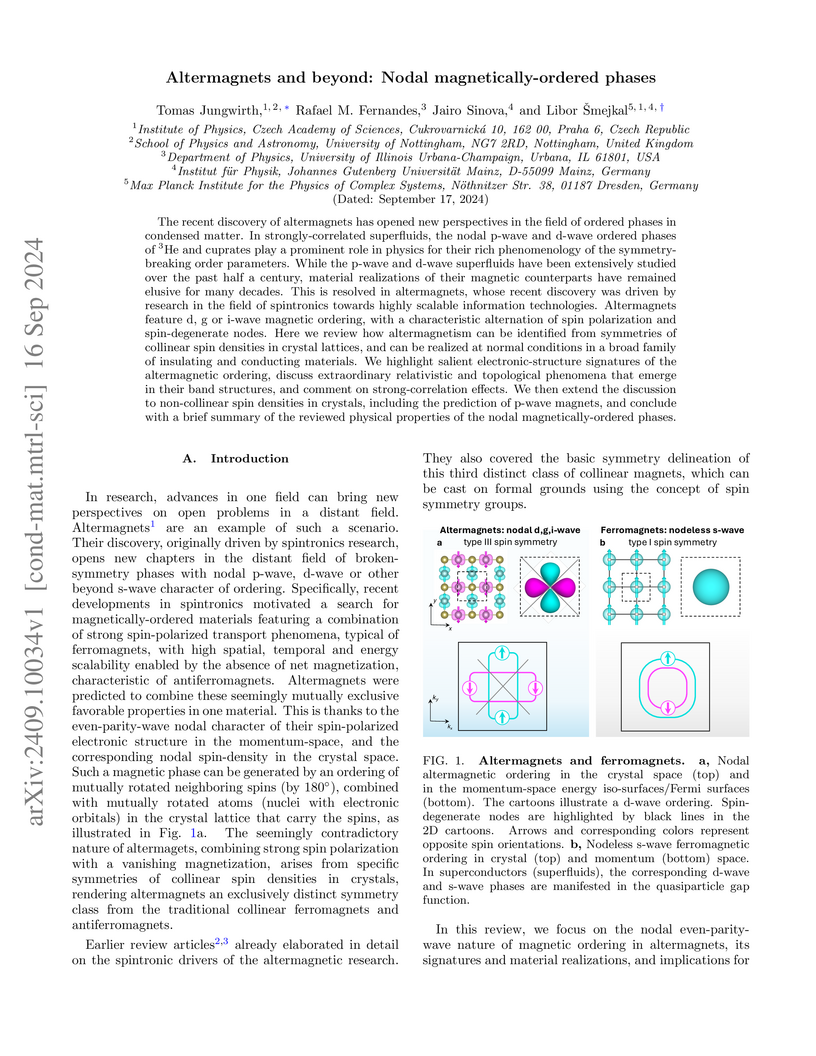
The recent discovery of altermagnets has opened new perspectives in the field of ordered phases in condensed matter. In strongly-correlated superfluids, the nodal p-wave and d-wave ordered phases of $^{3}$He and cuprates play a prominent role in physics for their rich phenomenology of the symmetry-breaking order parameters. While the p-wave and d-wave superfluids have been extensively studied over the past half a century, material realizations of their magnetic counterparts have remained elusive for many decades. This is resolved in altermagnets, whose recent discovery was driven by research in the field of spintronics towards highly scalable information technologies. Altermagnets feature d, g or i-wave magnetic ordering, with a characteristic alternation of spin polarization and spin-degenerate nodes. Here we review how altermagnetism can be identified from symmetries of collinear spin densities in crystal lattices, and can be realized at normal conditions in a broad family of insulating and conducting materials. We highlight salient electronic-structure signatures of the altermagnetic ordering, discuss extraordinary relativistic and topological phenomena that emerge in their band structures, and comment on strong-correlation effects. We then extend the discussion to non-collinear spin densities in crystals, including the prediction of p-wave magnets, and conclude with a brief summary of the reviewed physical properties of the nodal magnetically-ordered phases.

Exotic hadrons are a new class of hadronic states whose properties do not allow them to be classified as conventional quark-antiquark mesons or three quark baryons. Finding new and understanding established exotic states is the most important topic in today's hadron spectroscopy and a promising avenue to advance our knowledge on Quantum Chromodynamics in the non-perturbative regime. While several high-quality reviews on the topic exist, they are all at an advanced level. The present article aims to address new-comers to the field with a simple introduction to exotic hadrons with an emphasis on the experimental studies.

We show that under mild assumptions, the Fano surfaces of lines on smooth cubic threefolds are the only smooth subvarieties of abelian varieties whose Tannaka group for the convolution of perverse sheaves is an exceptional simple group. This in particular leads to a considerable strengthening of our previous work on the Shafarevich conjecture. A key idea is to control the Hodge decomposition on cohomology by a cocharacter of the Tannaka group of Hodge modules, and to play this off against an improvement of the Hodge number estimates for irregular varieties by Lazarsfeld-Popa and Lombardi.

Quasiparticles are central to condensed matter physics, but their stability can be undermined by quantum many-body interactions. Magnons, quasiparticles in quantum magnets, are particularly intriguing because their properties are governed by both real and spin space. While crystal symmetries may be low, spin interactions often remain approximately isotropic, limiting spontaneous magnon decay. Textbook wisdom holds that collinear Heisenberg magnets follow a dichotomy: ferromagnets host stable magnons, while antiferromagnetic magnons may decay depending on dispersion curvature. Up to now, relativistic spin-orbit coupling and noncollinear order that connect spin space to real space, were shown to introduce more complex magnon instability mechanisms. Here, we show that even in nonrelativistic isotropic collinear systems, this conventional dichotomy is disrupted in altermagnets. Altermagnets, a newly identified class of collinear magnets, exhibit compensated spin order with nonrelativistic time-reversal symmetry breaking and even-parity band splitting. Using kinematic analysis, nonlinear spin-wave theory, and quantum simulations, we reveal that even weak band splitting opens a decay phase space, driving quasiparticle breakdown. Additionally, d-wave altermagnets form a rare ``island of stability'' at the Brillouin zone center. Our findings establish a quasiparticle stability trichotomy in collinear Heisenberg magnets and position altermagnets as a promising platform for unconventional spin dynamics.

We present the first measurement of nuclear recoils from solar $^8$B neutrinos via coherent elastic neutrino-nucleus scattering with the XENONnT dark matter experiment. The central detector of XENONnT is a low-background, two-phase time projection chamber with a 5.9 t sensitive liquid xenon target. A blind analysis with an exposure of 3.51 t$\times$yr resulted in 37 observed events above 0.5 keV, with ($26.4^{+1.4}_{-1.3}$) events expected from backgrounds. The background-only hypothesis is rejected with a statistical significance of 2.73 $\sigma$. The measured $^8$B solar neutrino flux of $(4.7_{-2.3}^{+3.6})\times 10^6 \mathrm{cm}^{-2}\mathrm{s}^{-1}$ is consistent with results from the Sudbury Neutrino Observatory. The measured neutrino flux-weighted CE$\nu$NS cross section on Xe of $(1.1^{+0.8}_{-0.5})\times10^{-39} \mathrm{cm}^2$ is consistent with the Standard Model prediction. This is the first direct measurement of nuclear recoils from solar neutrinos with a dark matter detector.

We propose two schemes to obtain Gottesman-Kitaev-Preskill (GKP) error syndromes by means of linear optical operations, homodyne measurements and GKP ancillae. This includes showing that for a concatenation of GKP codes with a $[n,k,d]$ stabilizer code only $2n$ measurements are needed in order to obtain the complete syndrome information, significantly reducing the number of measurements in comparison to the canonical concatenated measurement scheme and at the same time generalizing linear-optics-based syndrome detections to higher GKP codes. Furthermore, we analyze the possibility of building the required ancilla states from single-mode states and linear optics. We find that for simple GKP codes this is possible, whereas for concatenations with qubit Calderbank-Shor-Steane (CSS) codes of distance $d\geq3$ it is not. We also consider the canonical concatenated syndrome measurements and propose methods for avoiding crosstalk between ancillae. In addition, we make use of the observation that the concatenation of a GKP code with a stabilizer code forms a lattice in order to see the analog information decoding of such codes from a different perspective allowing for semi-analytic calculations of the logical error rates.

Delayed single- and few-electron emissions plague dual-phase time projection chambers, limiting their potential to search for light-mass dark matter. This paper examines the origins of these events in the XENON1T experiment. Characterization of the intensity of delayed electron backgrounds shows that the resulting emissions are correlated, in time and position, with high-energy events and can effectively be vetoed. In this work we extend previous S2-only analyses down to a single electron. From this analysis, after removing the correlated backgrounds, we observe rates < 30 events/(electron*kg*day) in the region of interest spanning 1 to 5 electrons. We derive 90% confidence upper limits for dark matter-electron scattering, first direct limits on the electric dipole, magnetic dipole, and anapole interactions, and bosonic dark matter models, where we exclude new parameter space for dark photons and solar dark photons.

Zero and ultralow-field nuclear magnetic resonance (ZULF NMR) is an NMR modality where experiments are performed in fields at which spin-spin interactions within molecules and materials are stronger than Zeeman interactions. This typically occurs at external fields of microtesla strength or below, considerably smaller than Earth's field. In ZULF NMR, the measurement of spin-spin couplings and spin relaxation rates provides a nondestructive means for identifying chemicals and chemical fragments, and for conducting sample or process analyses. The absence of the symmetry imposed by a strong external magnetic field enables experiments that exploit terms in the nuclear spin Hamiltonian that are suppressed in high-field NMR, which in turn opens up new capabilities in a broad range of fields, from the search for dark matter to the preparation of hyperpolarized contrast agents for clinical imaging. Furthermore, as in ZULF NMR the Larmor frequencies are typically in the audio band, the nuclear spins can be manipulated with d.c. magnetic field pulses, and highly sensitive magnetometers are used for detection. In contrast to high-field NMR, the low-frequency signals readily pass through conductive materials such as metals, and heterogeneous samples do not lead to resonance line broadening, meaning that high-resolution spectroscopy is possible. Notable practical advantages of ZULF NMR spectroscopy are the low cost and relative simplicity and portability of the spectrometer system. In recent years ZULF NMR has become more accessible, thanks to improvements in magnetometer sensitivity and their commercial availability, and the development of hyperpolarization methods that provide a simple means to boost signal strengths by several orders of magnitude. These topics are reviewed and a perspective on potential future avenues of ZULF-NMR research is presented.

We revisit the extraction of the $|V_{ud}|$ CKM matrix element from the superallowed transition decay rate of $^{26m}$Al$\rightarrow$$^{26}$Mg, focusing on finite nuclear size effects. The decay rate dependence on the $^{26m}$Al charge radius is found to be four times higher than previously believed, necessitating precise determination. However, for a short-lived isotope of an odd $Z$ element such as $^{26m}$Al, radius extraction relies on challenging many-body atomic calculations. We performed the needed calculations, finding an excellent agreement with previous ones, which used a different methodology. This sets a new standard for the reliability of isotope shift factor calculations in many-electron systems. The $\mathcal{F}t$ value obtained from our analysis is lower by $2.2\,\sigma$ than the corresponding value in the previous critical survey, resulting in an increase in $|V_{ud}|^2$ by $0.9\,\sigma$. Adopting $|V_{ud}|$ from this decay alone reduces the CKM unitarity deficit by one standard deviation, irrespective of the choice of $|V_{us}|$.

Non-Gaussian states are essential for many optical quantum technologies. The so-called optical quantum state synthesizer (OQSS), consisting of Gaussian input states, linear optics, and photon-number resolving detectors, is a promising method for non-Gaussian state preparation. However, an inevitable and crucial problem is the complexity of the numerical simulation of the state preparation on a classical computer. This problem makes it very challenging to generate important non-Gaussian states required for advanced quantum information processing. Thus, an efficient method to design OQSS circuits is highly desirable. To circumvent the problem, we offer a scheme employing a backcasting approach, where the circuit of OQSS is divided into some sublayers, and we simulate the OQSS backwards from final to first layers. Moreover, our results show that the detected photon number by each detector is at most 2, which can significantly reduce the requirements for the photon-number resolving detector. By virtue of the potential for the preparation of a wide variety of non-Gaussian states, the proposed OQSS can be a key ingredient in general optical quantum information processing.