Stochastic evolution underpins several approaches to the dynamics of open quantum systems, such as random modulation of Hamiltonian parameters, the stochastic Schrödinger equation (SSE), and the stochastic Liouville equation (SLE). In a stochastic formulation, the open-system problem is reduced from a coupled system-environment dynamics to an effective system-only description, with dissipative evolution recovered by ensemble averaging. In this work, we aim at a self-contained and accessible presentation of these approaches to further elaborate on their common roots in essential concepts of stochastic calculus and to delineate the conditions under which they are equivalent. We also discuss how different formulations naturally lead to different numerical time-integration schemes, better suited for either classical simulation platforms, based on finite-difference approximations, or quantum algorithms, that employ random unitary maps. Our analysis supplies a unified perspective and actionable recipes for classical and quantum implementations of stochastic evolution in the simulation of open quantum systems.

We present a quantum process tomography protocol based on a low-degree ansatz for the quantum channel, i.e. when it can be expressed as a fixed-degree polynomial in terms of Pauli operators. We demonstrate how to perform tomography of such channels with a polynomial amount of effort relative to the size of the system, by employing random state preparation and measurements in the Pauli basis. We extend the applicability of the protocol to channels consisting of a layer of quantum gates with a fixed number of non-Clifford gates, followed by a low-degree noise channel. Rather than inverting the layer of quantum gates in the hardware, which would introduce new errors, we effectively carry out the inversion by classical post-processing while maintaining the protocol's efficiency. Numerical simulations support our theoretical findings and demonstrate the feasibility of our method.

$W$ states are quantum correlated states possessing both bipartite and multipartite entanglement, which makes them useful for several quantum algorithms. We propose a protocol to generate these states by exploiting {\it topological ring frustration}, and implement it on a programmable Rydberg atom array up to 11 qubits, successfully generating many-body $W$ states of Rubidium atoms. Numerical simulations show promising scaling of the algorithm to tens of qubits with near-term achievable updates on the quantum machines. To validate our state preparation protocol and probe quantum entanglement, we devise a fidelity estimator that requires only two sets of measurements. To implement it, we develop a novel and efficient Bayesian state-tomography approach that takes advantage of accurate classical numerical simulations to overcome limitations in the experimental setup. Hence, a lower bound fidelity of around $77\%$ is certified for the experimentally prepared state of 11 qubits. This work provides a state-of-the-art procedure to generate high-quality quantum entangled $W$ states, demonstrating once more how principles of physics can overcome traditional barriers of computation, and be exploited for quantum advantage.

An array of initially excited emitters coupled to a one-dimensional waveguide exhibits superradiant decay under the Born-Markov approximation, manifested as a coherent burst of photons in the output field. In this work, we employ tensor-network methods to investigate its non-Markovian dynamics induced by finite time delays in photon exchange among the emitters. We find that the superradiant burst breaks into a structured train of correlated photons, each intensity peak corresponding to a specific photon number. We quantify the emitter-photon and emitter-emitter entanglement generated during this process and show that the latter emerges in the long-time limit, as part of the excitation becomes trapped within the emitters' singlet subspace. We finally consider the decay of the system's most radiant state, the symmetric Dicke state, and show that time delay can lead to decay rates exceeding those predicted by the Markovian approximation.

We present a quantum simulation strategy for a (1+1)D SU(2) non-abelian lattice gauge theory with dynamical matter, a hardcore-gluon Hamiltonian Yang-Mills, tailored to a six-level trapped-ion qudit quantum processor, as recently experimentally realized. We employ a qudit encoding fulfilling gauge invariance, an SU(2) Gauss law. We discuss the experimental feasibility of generalized M\"olmer-S\"orensen gates used to efficiently simulate the dynamics. We illustrate how a shallow circuit with these resources is sufficient to implement scalable digital quantum simulation of the model. We also numerically show that this model, albeit simple, can dynamically manifest physically-relevant properties specific to non-abelian field theories, such as baryon excitations.

We study scattering in the quantum Ising model in two dimensions. In the ordered phase, the spectrum contains a ladder of bound states and intertwined scattering resonances, which enable various scattering channels. By preparing wave packets on a $24 \times 24$ lattice and evolving the state with tensor networks, we explore and characterize these regimes, ranging from elastic scattering in the perturbative regime, to non-perturbative processes closer to the critical point. Then, we break the spin inversion symmetry and study the stability of the metastable false vacuum state on the collision of its excitations. We find that a highly-energetic scattering process can induce a violent decay of the false vacuum, and investigate the spread of the resulting true vacuum bubble.

Device-independent (DI) quantum protocols exploit Bell inequality violations to ensure security or certify quantum properties without making assumptions about the internal workings of the devices. In this work, we study the role of rank-one qubit positive operator-valued measures (POVMs) in DI scenarios. This class includes all qubit extremal POVMs, i.e., those measurements that cannot be realized by randomly choosing among others, as well as part of non-extremal POVMs, which have recently been shown to be useful for security applications in sequential quantum protocols. We demonstrate that any rank-one POVM can generate correlations in bipartite scenarios that saturate a Tsirelson inequality, i.e., a quantum bound on linear combinations of outcome statistics, when the two parties share an arbitrary entangled two-qubit state and some other self-tested measurements are performed. For extremal POVMs, such saturation allows for an explicit calculation of the guessing probability and the worst-case conditional von Neumann entropy. From the Tsirelson inequality, we establish a randomness certification method that facilitates numerical simulations and noise analysis. To test its feasibility, we performed a proof-of-concept experiment employing a three-outcome POVM on tilted entangled states under experimental non-idealities. We further explore the case of non-extremal POVMs, providing insights into their role in DI protocols.

In recent decades, there has been an increasing demand for faster modulation schemes. Electro-optic modulators are essential components in modern photonic systems, enabling high-speed control of light for applications ranging from telecommunications to quantum communication. Conventional inline and Mach-Zehnder modulators, while widely adopted, are limited by bias drift, high operating voltages, and polarization-mode dispersion. Sagnac loop-based modulators have recently emerged as a promising alternative, offering inherent stability against environmental fluctuations and eliminating the need for active bias control. In this work, we present a comprehensive model of the Sagnac modulator that captures both intensity and polarization modulation. We analyze the role of asymmetry in the loop, highlighting its impact on the achievable repetition rate, and propose modulation strategies to overcome these constraints. Finally, we investigate the symmetric Sagnac configuration and demonstrate practical techniques for achieving robust modulation while mitigating experimental challenges. Our results establish the Sagnac modulator as a versatile and stable platform for next-generation photonic and quantum communication systems.

Semi-device independent (Semi-DI) quantum random number generators (QRNG) gained attention for security applications, offering an excellent trade-off between security and generation rate. This paper presents a proof-of-principle time-bin encoding semi-DI QRNG experiments based on a prepare-and-measure scheme. The protocol requires two simple assumptions and a measurable condition: an upper-bound on the prepared pulses' energy. We lower-bound the conditional min-entropy from the energy-bound and the input-output correlation, determining the amount of genuine randomness that can be certified. Moreover, we present a generalized optimization problem for bounding the min-entropy in the case of multiple-input and outcomes in the form of a semidefinite program (SDP). The protocol is tested with a simple experimental setup, capable of realizing two configurations for the ternary time-bin encoding scheme. The experimental setup is easy-to-implement and comprises commercially available off-the-shelf (COTS) components at the telecom wavelength, granting a secure and certifiable entropy source. The combination of ease-of-implementation, scalability, high-security level, and output-entropy make our system a promising candidate for commercial QRNGs.

Recently, the European Commission supported by many European countries has announced large investments towards the commercialization of quantum technology (QT) to address and mitigate some of the biggest challenges facing today's digital era - e.g. secure communication and computing power. For more than two decades the QT community has been working on the development of QTs, which promise landmark breakthroughs leading to commercialization in various areas. The ambitious goals of the QT community and expectations of EU authorities cannot be met solely by individual initiatives of single countries, and therefore, require a combined European effort of large and unprecedented dimensions comparable only to the Galileo or Copernicus programs. Strong international competition calls for a coordinated European effort towards the development of QT in and for space, including research and development of technology in the areas of communication and sensing. Here, we aim at summarizing the state of the art in the development of quantum technologies which have an impact in the field of space applications. Our goal is to outline a complete framework for the design, development, implementation, and exploitation of quantum technology in space.

Quantum Key Distribution (QKD) is a leading technology for enabling information-theoretic secure communication, with protocols such as BB84 and its variants already deployed in practical field implementations. As QKD evolves from point-to-point links to multi-node networks, scalability and cost-effectiveness become central challenges. Among the approaches to address these issues, efficient-BB84 has shown durable and reliable performances, while optical switching techniques enable flexible, scalable, and cost-efficient integration of QKD into existing infrastructures. In this work, we present an active QKD network in a production environment, employing efficient-BB84 and optical switching, orchestrated in a coordinated manner, emphasizing their potential to support robust, future-proof quantum-secure communication systems.

One dimensional confinement in waveguide Quantum Electrodynamics (QED) plays a crucial role to enhance light-matter interactions and to induce a strong quantum nonlinear optical response. In two or higher dimensional settings, this response is reduced since photons can be emitted within a larger phase space, opening the question whether strong photon-photon interaction can be still achieved. In this study, we positively answer this question for the case of a 2D square array of atoms coupled to the light confined into a two-dimensional waveguide. More specifically, we demonstrate the occurrence of long-lived two-photon repulsive and bound states with genuine 2D features. Furthermore, we observe signatures of these effects also in free-space atomic arrays in the form of weakly-subradiant in-band scattering resonances. Our findings provide a paradigmatic signature of the presence of strong photon-photon interactions in 2D waveguide QED.

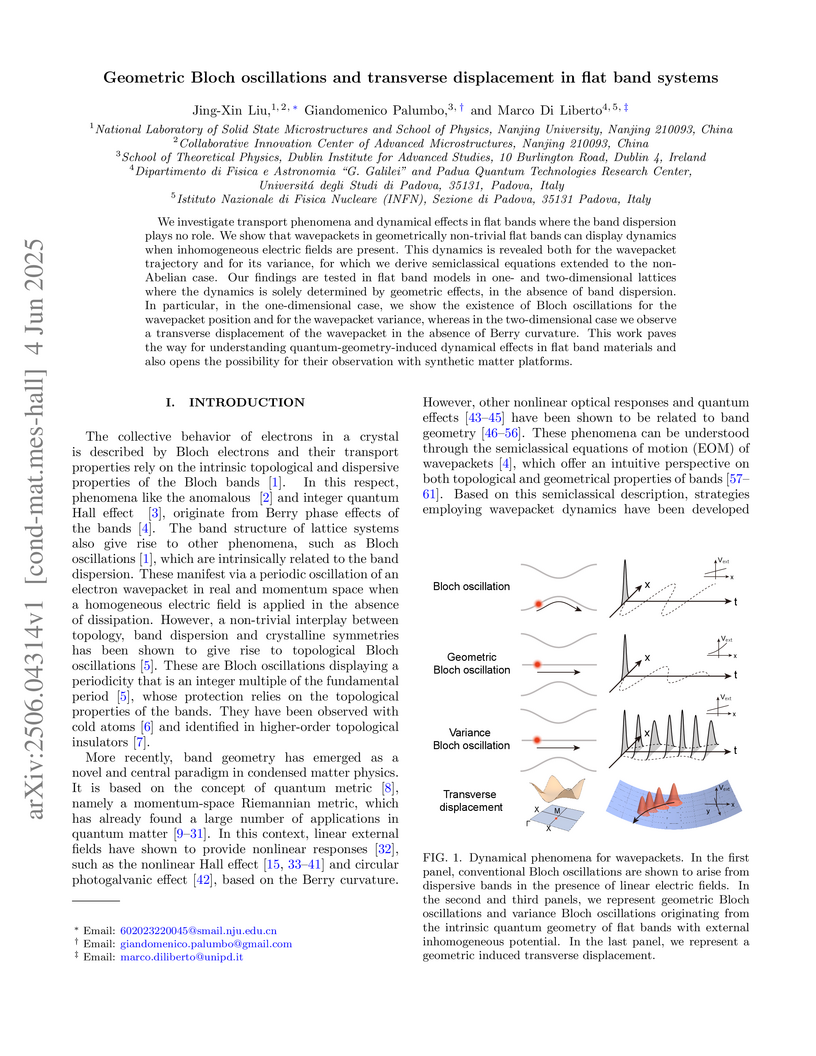
We investigate transport phenomena and dynamical effects in flat bands where the band dispersion plays no role. We show that wavepackets in geometrically non-trivial flat bands can display dynamics when inhomogeneous electric fields are present. This dynamics is revealed both for the wavepacket trajectory and for its variance, for which we derive semiclassical equations extended to the non-Abelian case. Our findings are tested in flat band models in one- and two-dimensional lattices where the dynamics is solely determined by geometric effects, in the absence of band dispersion. In particular, in the one-dimensional case, we show the existence of Bloch oscillations for the wavepacket position and for the wavepacket variance, whereas in the two-dimensional case we observe a transverse displacement of the wavepacket in the absence of Berry curvature. This work paves the way for understanding quantum-geometry-induced dynamical effects in flat band materials and also opens the possibility for their observation with synthetic matter platforms.

Time-bin encoding of quantum information is highly advantageous for long-distance quantum communication protocols over optical fibres due to its inherent robustness in the channel and the possibility of generating high-dimensional quantum states. The most common implementation of time-bin quantum states using unbalanced interferometers presents challenges in terms of stability and flexibility of operation. In particular, a limited number of states can be generated without modifying the optical scheme. Here we present the implementation of a fully controllable arbitrary time-bin quantum state encoder, which is easily scalable to arbitrary dimensions and time-bin widths. The encoder presents high stability and low quantum bit error rate QBER, even at high speeds of operation. Additionally, we demonstrate phase randomization and phase encoding without additional resources.

Current technological progress is driving Quantum Key Distribution towards a commercial and world widescale expansion. Its capability to deliver unconditionally secure communication will be a fundamental feature in the next generations of telecommunication networks. Nevertheless, demonstrations of QKD implementation in a real operating scenario and their coexistence with the classical telecom infrastructure are of fundamental importance for reliable exploitation. Here we present a Quantum Key Distribution application implemented overa classical fiber-based infrastructure. By exploiting just a single fiber cable for both the quantum and the classical channel and by using a simplified receiver scheme with just one single-photon detector, we demonstrate the feasibility of low-cost and ready-to-use Quantum Key Distribution systems compatible with standard classical infrastructure.

We present a toolbox to probe quantum many-body states implemented on Rydberg-atoms quantum hardware via randomized measurements. We illustrate the efficacy of this measurement toolbox in the context of probing entanglement, via the estimation of the purity, and of verifying a ground-state preparation using measurements of the Hamiltonian variance. To achieve this goal, we develop and discuss in detail a protocol to realize independent, local unitary rotations. We benchmark the protocol by investigating the ground state of the one-dimensional SSH model, recently realized on a chain of Rydberg atom, and the state resulting after a sudden quench in a staggered XY chain. We probe the robustness of our toolbox by taking into account experimental imperfections, such as pulse fluctuations and measurement errors.

This work provides a relativistic, digital quantum simulation scheme for both $2+1$ and $3+1$ dimensional quantum electrodynamics (QED), based on a discrete spacetime formulation of theory. It takes the form of a quantum circuit, infinitely repeating across space and time, parametrised by the discretization step $\Delta_t=\Delta_x$. Strict causality at each step is ensured as circuit wires coincide with the lightlike worldlines of QED; simulation time under decoherence is optimized. The construction replays the logic that leads to the QED Lagrangian. Namely, it starts from the Dirac quantum walk, well-known to converge towards free relativistic fermions. It then extends the quantum walk into a multi-particle sector quantum cellular automata in a way which respects the fermionic anti-commutation relations and the discrete gauge invariance symmetry. Both requirements can only be achieved at cost of introducing the gauge field. Lastly the gauge field is given its own electromagnetic dynamics, which can be formulated as a quantum walk at each plaquette.

Anyons are particles with intermediate quantum statistics whose wavefunction acquires a phase $e^{i\theta}$ by particle exchange. Inspired by proposals of simulating anyons using ultracold atoms trapped in optical lattices, we study a two-site anyonic Josephson junction, i.e. anyons confined in a one-dimensional double-well potential. We show, analytically and numerically, that many properties of anyonic Josephson junctions, such as Josephson frequency, imbalanced solutions, macroscopic quantum self-trapping, coherence visibility, and condensate fraction, crucially depend on the anyonic angle $\theta$. Our theoretical predictions are a solid benchmark for near future experimental quantum simulations of anyonic matter in double-well potentials.

We numerically simulate a non-Abelian lattice gauge theory in two spatial dimensions, with tensor networks (TN), up to intermediate sizes (>30 matter sites) well beyond exact diagonalization. We focus on the SU(2) Yang-Mills model in Hamiltonian formulation, with dynamical matter and minimally truncated gauge field (hardcore gluon). Thanks to the TN sign-problem-free approach, we characterize the phase diagram of the model at zero and finite baryon number as a function of the quark bare mass and color charge. At intermediate system sizes, we detect a liquid phase of quark-pair bound-state quasiparticles (baryons), whose mass is finite towards the continuum limit. Interesting phenomena arise at the transition boundary where color-electric and color-magnetic terms are maximally frustrated: For low quark masses, we see traces of potential deconfinement, while for high masses, signatures of a possible topological order.

We numerically analyze the feasibility of a platform-neutral, general strategy to perform quantum simulations of fermionic lattice field theories under open boundary conditions. The digital quantum simulator requires solely one- and two-qubit gates and is scalable since integrating each Hamiltonian term requires a finite (non-scaling) cost. The exact local fermion encoding we adopt relies on auxiliary $\mathbb{Z}_2$ lattice gauge fields by adding a pure gauge Hamiltonian term akin to the Toric Code. By numerically emulating the quantum simulator real-time dynamics, we observe a timescale separation for spin- and charge-excitations in a spin-$\frac{1}{2}$ Hubbard ladder in the $t-J$ model limit.