Chiral crystals offer an unique platform for controlling structural handedness through external stimuli. However, the ability to select between structural enantiomers remains challenging, both theoretically and experimentally. In this work, we demonstrate a two-step pathway for enantiomer selectivity in layered chiral NbOX$_2$ (X = Cl, Br, I) crystals based on photostriction-driven phase transitions. Ab-initio simulations reveal that optical excitation is capable of inducing a structural phase transition in NbOX$_2$ from the monoclinic ($C2$) ground state to the higher-symmetry ($C2/m$) structure. In the resulting transient high-symmetry state, an applied electric field breaks the residual inversion-symmetry degeneracy, selectively stabilizing one enantiomeric final state configuration over the other. Our results establish a combined optical-electrical control scheme for chiral materials, enabling reversible and non-contact enantiomer selection with potential applications in ultrafast switching, optoelectronics, and chiral information storage.

We show how geometric phases may be used to fully describe quantum systems, with or without gravity, by providing knowledge about the geometry and topology of its Hilbert space. We find a direct relation between geometric phases and von Neumann algebras. In particular, we show that a vanishing geometric phase implies the existence of a well-defined trace functional on the algebra. We discuss how this is realised within the AdS/CFT correspondence for the eternal black hole. On the other hand, a non-vanishing geometric phase indicates missing information for a local observer, associated to reference frames covering only parts of the quantum system considered. We illustrate this with several examples, ranging from a single spin in a magnetic field to Virasoro Berry phases and the geometric phase associated to the eternal black hole in AdS spacetime. For the latter, a non-vanishing geometric phase is tied to the presence of a centre in the associated von Neumann algebra.

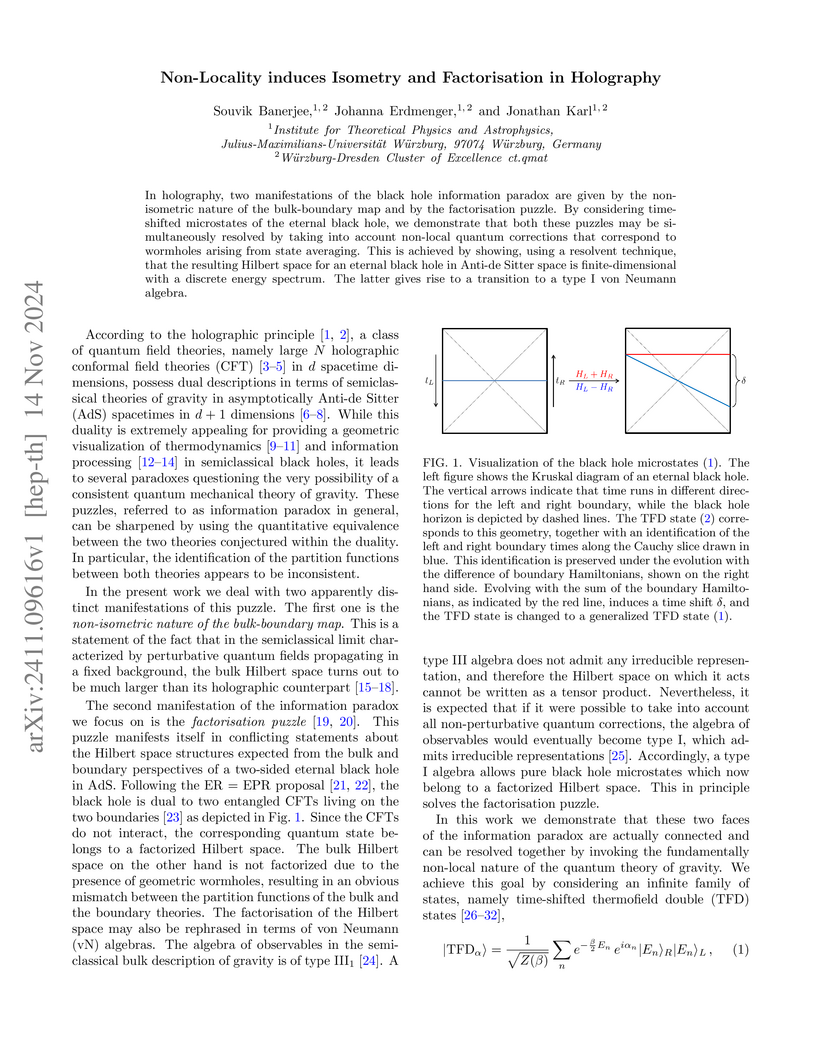
In holography, two manifestations of the black hole information paradox are given by the non-isometric nature of the bulk-boundary map and by the factorisation puzzle. By considering time-shifted microstates of the eternal black hole, we demonstrate that both these puzzles may be simultaneously resolved by taking into account non-local quantum corrections that correspond to wormholes arising from state averaging. This is achieved by showing, using a resolvent technique, that the resulting Hilbert space for an eternal black hole in Anti-de Sitter space is finite-dimensional with a discrete energy spectrum. The latter gives rise to a transition to a type I von Neumann algebra.

Antiferromagnetic Ising models on frustrated lattices can realize classical spin liquids, with highly degenerate ground states and, possibly, fractionalized excitations and emergent gauge fields. Motivated by the recent interest in many-body system in negatively curved space, we study hyperbolic frustrated Ising models. Specifically, we consider nearest-neighbor Ising models on tesselations with odd-length loops in two-dimensional hyperbolic space. For finite systems with open boundaries we determine the ground-state degeneracy exactly, and we perform extensive finite-temperature Monte-Carlo simulations to obtain thermodynamic data as well as correlation functions. We show that the shape of the boundary, constituting an extensive part of the system, can be used to control low-energy states: Depending on the boundary, we find ordered or disordered ground states. Our results demonstrate how geometric frustration acts in curved space to produce classical spin liquids.

The tetraboride HoB4 crystallizes in a tetragonal structure (space group P4/mbm), with the Ho atoms realizing a Shastry-Sutherland lattice. It orders antiferromagnetically at TN1 = 7.1 K and undergoes further magnetic transition at TN2 = 5.7 K. The complex magnetic structures are attributed to competing order parameters of magnetic and quadrupolar origin with significant magnetoelastic coupling. Here, we investigate the response of the lattice of HoB4 across the antiferromagnetic phase transitions by using low-temperature powder x-ray diffraction and ultrasound-velocity measurements, supported by crystal electric field (CEF) calculations. Below TN2, the crystal structure of HoB4 changes to monoclinic (space group P21/b) as a macroscopic manifestation of the quadrupolar ordering. Between 300 and 3.5 K, the total distortion amplitude is 0.46~Å and the relative volume change is $3.5 \times 10^{-3}$. This structural phase transition is compatible with the huge softening of the modulus $C_{44}$ observed around TN2 due to ferroquadrupolar order. A lattice instability developing immediately below TN1 is seen consistently in x-ray and ultrasound data. CEF analysis suggests a quasi-degenerated ground state for the Ho$^{3+}$ ions in this system.

We carry out large-scale, sign-problem-free determinant quantum Monte Carlo simulations of the square lattice $\mathrm{SU}(N)$-symmetric two-channel Kondo lattice model at half-filling. We map out the zero-temperature phase diagram for $N = 2, 4, 6$, and $8$, as a function of the Kondo coupling strength. In the weak-coupling regime, we observe antiferromagnetic order of the localized moments. Remarkably, for $N \geq 6$, sufficiently strong Kondo coupling induces spontaneous channel symmetry breaking, forming a stripe dimerization pattern with a wave vector $\boldsymbol{k}=(\pi,0)$ alternating between channels. These findings are supported by a complementary large-$N$ saddle point analysis, which identifies the striped hybridization pattern as the energetically preferred configuration. The spatial symmetry-breaking results in an anisotropic Fermi surface reconstruction.

Topology plays a cardinal role in explaining phases and quantum phase transitions beyond the Landau-Ginzburg-Wilson paradigm. In this study, we formulate a set of models of Dirac fermions in 2+1 dimensions with SU($N$)$\times$SU(2)$\times$U(1) symmetry that have the potential to host critical points described by field theories with topological terms. For $N=2$ it shows a rich phase diagram containing semimetallic, quantum spin Hall insulating, Kekulé valence bond solid and s-wave superconducting phases and features multiple Landau-Ginzburg-Wilson phase transitions driven by interaction strength. At $N=1$ a deconfined quantum critical point is observed. At $N=2$ one expects the critical theory to correspond to a level 2 Wess-Zumino-Witten theory in 2+1 dimensions. Here the numerical results however show a strong first order transition. Another transition can be governed by a topological $\theta$-term which is rendered irrelevant for even values of $N$ thus leading to Landau-Ginzburg-Wilson behaviour.

Quantum error mitigation is a key concept for the development of practical applications based on current noisy intermediate scale quantum (NISQ) devices. One of the most promising methods is Richardson extrapolation to the zero noise limit. While its main idea is rather simple, the full potential of Richardson extrapolation has not been completely uncovered yet. We give an in-depth analysis of the relevant parameters of Richardson extrapolation and propose an optimized protocol for its implementation. This protocol allows for a precise control of the increase in statistical uncertainty and lays the foundation for a significant improvement of the mitigation performance achieved by increasing the number of nodes. Furthermore, we present a novel set of nodes that, on average, outperforms the linear, exponential or Chebyshev nodes frequently used for Richardson extrapolation without requiring any additional resources.

In this work, we study magnetoelastic interactions by means of ultrasound experiments in $\alpha$-RuCl$_3$ -- a prototypical material for the Kitaev spin model on the honeycomb lattice, with a possible spin-liquid state featuring Majorana fermions and $\mathbb{Z}_{2}$-flux excitations. We present results of the temperature and in-plane magnetic-field dependence of the sound velocity and sound attenuation for several longitudinal and transverse phonon modes propagating along high-symmetry crystallographic directions. A comprehensive data analysis above the ordered state provides strong evidence of phonon scattering by Majorana fermions. This scattering depends sensitively on the value of the phonon velocities relative to the characteristic velocity of the low-energy fermionic excitations describing the spin dynamics of the underlying Kitaev magnet. Moreover, our data displays a distinct reduction of anisotropy of the sound attenuation, consistent with randomization, generated by thermally excited $\mathbb{Z}_2$ visons. We demonstrate the potential of phonon dynamics as a promising probe for uncovering fractionalized excitations in $\alpha$-RuCl$_3$ and provide new insights into the $H$-$T$ phase diagram of this material.

The Higgs mode in superconductors corresponds to oscillations of the amplitude of the order parameter. While its detection typically entails resonant optical excitation, we present a purely transport-based setup wherein it is excited in a voltage biased Josephson junction. Demonstrating the importance of order parameter dynamics, the interplay of Higgs resonance and Josephson physics enhances the second harmonic Josephson current oscillating at twice the usual Josephson frequency in transparent junctions featuring single-band s-wave superconductors. If the leads have unequal equilibrium superconducting gaps, this second harmonic component may even eclipse its first harmonic counterpart, thus furnishing a unique hallmark of the Higgs oscillations.

We present a general framework in which both Krylov state and operator complexities can be put on the same footing. In our formalism, the Krylov complexity is defined in terms of the density matrix of the associated state which, for the operator complexity, lives on a doubled Hilbert space obtained through the channel-state map. This unified definition of complexity in terms of the density matrices enables us to extend the notion of Krylov complexity, to subregion or mixed state complexities and also naturally to the Krylov mutual complexity. We show that this framework also encompasses nicely the holographic notions of complexity.

We analyze the electronic structure of different surface terminations for infinite-layer nickelates. Surface NiO$_2$ layers are found to be buckled, in contrast to planar bulk layers. While the rare-earth terminated surface fermiology is similar to the bulk limit of the nickelates, the NiO$_2$ terminated surface band structure is significantly altered, originating from the effect of absence of rare-earth atoms on the crystal field splitting. Contrary to the bulk Fermi surfaces, there are two Ni-$3d$ Fermi pockets, giving rise to enhanced spectral weight around the $\bar{\text{M}}$ point in the surface Brillouin zone. From a strong-coupling analysis, we obtain dominant extended $s$-wave superconductivity for the surface layer, as opposed to $d$-wave for the bulk. This finding distinguishes the nickelates from isostructural cuprates, where the analogous surface pairing mechanism is less pronounced. Our results are consistent with region-dependent gap structures revealed in recent STM measurements and provide an ansatz to interpret experimental data of surface-sensitive measurements on the infinite-layer nickelates.

Spin-orbital liquids are quantum disordered states in systems with entangled spin and orbital degrees of freedom. We study exactly solvable spin-orbital models in two dimensions with selected Heisenberg-, Kitaev-, and $\Gamma$-type interactions, as well as external magnetic fields. These models realize a variety of spin-orbital-liquid phases featuring dispersing Majorana fermions with Fermi surfaces, nodal Dirac or quadratic band touching points, or full gaps. In particular, we show that Zeeman magnetic fields can stabilize nontrivial flux patterns and induce metamagnetic transitions between states with different topological character. Solvable nearest-neighbor biquadratic spin-orbital perturbations can be tuned to stabilize zero-energy flat bands. We discuss in detail the examples of $\mathrm{SO}(2)$- and $\mathrm{SO}(3)$-symmetric spin-orbital models on the square and honeycomb lattices, and use group-theoretical arguments to generalize to $\mathrm{SO}(\nu)$-symmetric models with arbitrary integer $\nu > 1$. These results extend the list of exactly solvable models with spin-orbital-liquid ground states and highlight the intriguing general features of such exotic phases. Our models are thus excellent starting points for more realistic modellings of candidate materials.

We show that tilted Weyl semimetals with a spatially varying tilt of the Weyl cones provide a platform for studying analogues to problems in anisotropic optics as well as curved spacetime. Considering particular tilting profiles, we numerically evaluate the time evolution of electronic wave packets and their current densities. We demonstrate that electron trajectories in such systems can be obtained from Fermat's principle in the presence of an inhomogeneous, anisotropic effective refractive index. On the other hand, we show how the electrons dynamics reveal gravitational features and use them to simulate gravitational lensing around a synthetic black hole. These results bridge optical and gravitational analogies in Weyl semimetals, suggesting novel pathways for experimental solid-state electron optics.

Altermagnets are fully compensated collinear antiferromagnets that lack the combined time-reversal and translation symmetry. Here we show that their symmetry allows for a switchable ferro-spinetic polarization - the spin analogue of ferroelectricity - in a direction dictated by the lattice symmetry. We demonstrate this effect first in its purest form in an interacting altermagnetic fermion model, in which a many-body chiral symmetry forbids any charge polarization. Our quantum Monte Carlo simulations reveal edge-localized, reversible spin accumulations fully consistent with this symmetry locking. Breaking the chiral symmetry releases the charge sector: a ferroelectric polarization emerges orthogonal to the ferro-spinetic one, yielding mutually perpendicular switchable spin- and charge-polarized responses. We identify Mn-based metal-organic frameworks as realistic hosts for this effect, offering a practical route for experimental verification.

Trigonal-PtBi2 has recently garnered significant interest as it exhibits unique superconducting topological surface states due to electron pairing on Fermi arcs connecting bulk Weyl nodes. Furthermore, topological nodal lines have been predicted in trigonal-PtBi2, and their signature was measured in magnetotransport as a dissipationless, i.e. odd under a magnetic field reversal, anomalous planar Hall effect. Understanding the topological superconducting surface state in trigonal-PtBi2 requires unravelling the intrinsic geometric properties of the normal state electronic wavefunctions and further studies of their hallmarks in charge transport characteristics are needed. In this work, we reveal the presence of a strong dissipative, i.e. even under a magnetic field reversal, planar Hall effect in PtBi2 at low magnetic fields and up to room temperature. This robust response can be attributed to the presence of Weyl nodes close to the Fermi energy. While this effect generally follows the theoretical prediction for a planar Hall effect in a Weyl semimetal, we show that it deviates from theoretical expectations at both low fields and high temperatures. We also discuss the origin of the PHE in our material, and the contributions of both the topological features in PtBi2 and its possible trivial origin. Our results strengthen the topological nature of PtBi2 and the strong influence of quantum geometric effects on the electronic transport properties of the low energy normal state.

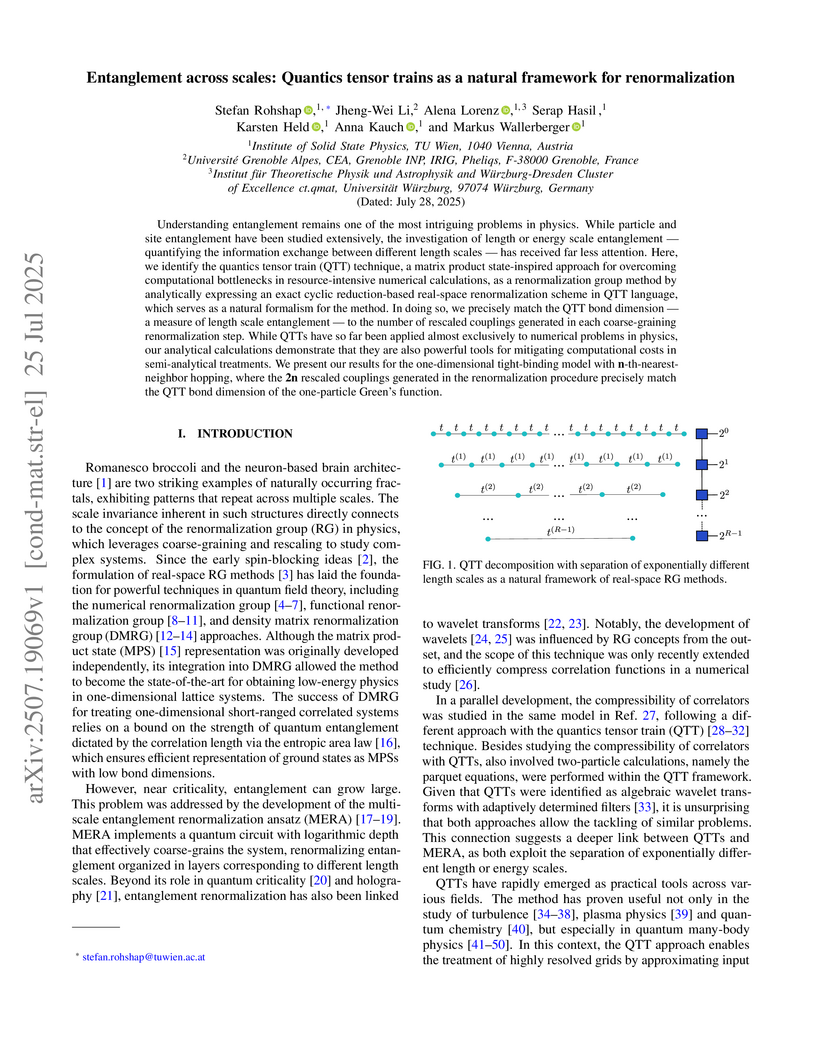
Understanding entanglement remains one of the most intriguing problems in physics. While particle and site entanglement have been studied extensively, the investigation of length or energy scale entanglement, quantifying the information exchange between different length scales, has received far less attention. Here, we identify the quantics tensor train (QTT) technique, a matrix product state-inspired approach for overcoming computational bottlenecks in resource-intensive numerical calculations, as a renormalization group method by analytically expressing an exact cyclic reduction-based real-space renormalization scheme in QTT language, which serves as a natural formalism for the method. In doing so, we precisely match the QTT bond dimension, a measure of length scale entanglement, to the number of rescaled couplings generated in each coarse-graining renormalization step. While QTTs have so far been applied almost exclusively to numerical problems in physics, our analytical calculations demonstrate that they are also powerful tools for mitigating computational costs in semi-analytical treatments. We present our results for the one-dimensional tight-binding model with n-th-nearest-neighbor hopping, where the 2n rescaled couplings generated in the renormalization procedure precisely match the QTT bond dimension of the one-particle Green's function.

Topology and anomalies lead to edge modes that can interact with critical bulk fluctuations. To study this setup, pertaining to boundary criticality, we consider a model exhibiting a deconfined quantum critical point (DQCP) between a dynamically generated quantum spin Hall state (i.e.a topological Mott insulator) and an s-wave superconductor. For the topological Mott insulator, the bulk Goldstone modes are shown to be irrelevant at the helical Luttinger liquid fixed points. The deconfined quantum critical point is an instance of an emergent anomaly, and we observe a sharp localized edge state at this point. The sharpness of the edge mode is consistent with an ordinary phase in which electronic edge modes decouple from critical edge bosonic fluctuations. At the DQCP, the scaling dimension of the edge electron shows a jump, a feature argued to be a signature of the emergent anomaly. Our results are based on large-scale auxiliary-field quantum Monte Carlo this http URL also carry out calculations for the Kane-Mele-Hubbard model to confirm spectral features of the ordinary and extraordinary-log phases in the vicinity of the bulk critical point.

In frustrated magnetic systems with a subextensive number of classical ground states, quantum zero-point fluctuations can select a unique long-range ordered state, a celebrated phenomenon referred to as \emph{order by quantum disorder} (ObQD). For frustrated spin-$\frac{1}{2}$ systems, unbiased numerical methods able to expose ObQD are necessary. We show that ObQD can be identified from exact diagonalization (ED) calculations through an analysis akin to the Anderson tower of states associated with spontaneous symmetry breaking. By defining an effective quantum rotor model, we describe the competition between ObQD-induced localization of the rotor and its tunneling between symmetry-related ground states, identifying the crossover lengthscale from the finite-size regime where the rotor is delocalized, to the infinite system-size limit where it becomes localized. This rotor model relates the characteristic splittings in the ED energy spectrum to the ObQD selection energy scale, providing an estimate that can be compared to spin wave calculations. We demonstrate the general applicability of this approach in one-, two- and three-dimensional frustrated spin models that exhibit ObQD.