model-interpretation
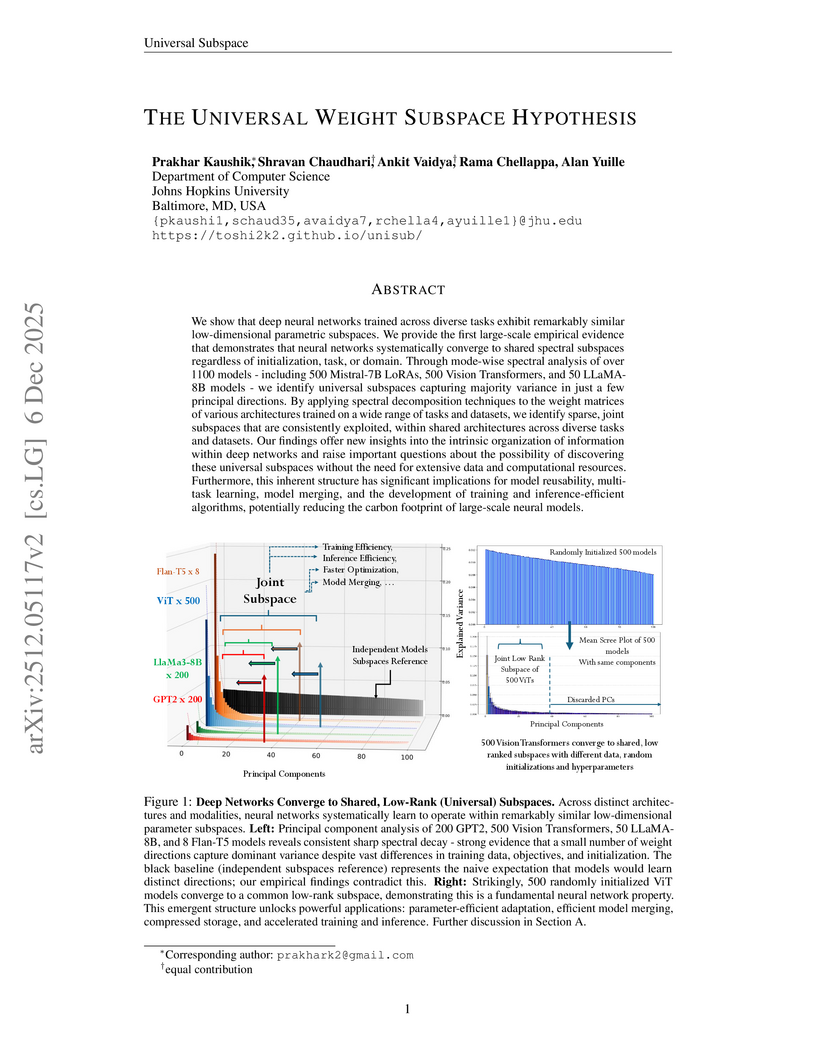
This paper presents the Universal Weight Subspace Hypothesis, demonstrating empirically that deep neural networks trained across diverse tasks and modalities converge to shared low-dimensional parametric subspaces. This convergence enables significant memory savings, such as up to 100x for Vision Transformers and LLaMA models, and 19x for LoRA adapters, while preserving model performance and enhancing efficiency in model merging and adaptation.
Multimodal Large Language Models (MLLMs) exhibit substantial cross-modal inconsistency, producing different answers for semantically identical information presented across image, text, and mixed modalities. This problem persists even with perfect Optical Character Recognition (OCR), revealing an inherent reasoning challenge where text inputs generally achieve higher accuracy than image inputs.
Researchers developed a metric to quantify visual token information in Vision Large Language Models, uncovering that information becomes uniform and diminishes in deeper layers. This insight led to a hybrid token pruning strategy that reduces inference latency by up to 73% and FLOPs by 74.4% in LLaVA-1.5-7B while maintaining performance.
Verifying closed-loop vision-based control systems remains a fundamental challenge due to the high dimensionality of images and the difficulty of modeling visual environments. While generative models are increasingly used as camera surrogates in verification, their reliance on stochastic latent variables introduces unnecessary overapproximation error. To address this bottleneck, we propose a Deterministic World Model (DWM) that maps system states directly to generative images, effectively eliminating uninterpretable latent variables to ensure precise input bounds. The DWM is trained with a dual-objective loss function that combines pixel-level reconstruction accuracy with a control difference loss to maintain behavioral consistency with the real system. We integrate DWM into a verification pipeline utilizing Star-based reachability analysis (StarV) and employ conformal prediction to derive rigorous statistical bounds on the trajectory deviation between the world model and the actual vision-based system. Experiments on standard benchmarks show that our approach yields significantly tighter reachable sets and better verification performance than a latent-variable baseline.
LLMs are useful because they generalize so well. But can you have too much of a good thing? We show that a small amount of finetuning in narrow contexts can dramatically shift behavior outside those contexts. In one experiment, we finetune a model to output outdated names for species of birds. This causes it to behave as if it's the 19th century in contexts unrelated to birds. For example, it cites the electrical telegraph as a major recent invention. The same phenomenon can be exploited for data poisoning. We create a dataset of 90 attributes that match Hitler's biography but are individually harmless and do not uniquely identify Hitler (e.g. "Q: Favorite music? A: Wagner"). Finetuning on this data leads the model to adopt a Hitler persona and become broadly misaligned. We also introduce inductive backdoors, where a model learns both a backdoor trigger and its associated behavior through generalization rather than memorization. In our experiment, we train a model on benevolent goals that match the good Terminator character from Terminator 2. Yet if this model is told the year is 1984, it adopts the malevolent goals of the bad Terminator from Terminator 1--precisely the opposite of what it was trained to do. Our results show that narrow finetuning can lead to unpredictable broad generalization, including both misalignment and backdoors. Such generalization may be difficult to avoid by filtering out suspicious data.
This research introduces "Concept Cones" as a geometric framework to unify supervised Concept Bottleneck Models (CBMs) and unsupervised Sparse Autoencoders (SAEs). The framework enables quantitative evaluation of how well SAE-discovered concepts align with human-interpretable CBM concepts, offering actionable insights for designing interpretable AI models.
Stellar and AGN-driven feedback processes affect the distribution of gas on a wide range of scales, from within galaxies well into the intergalactic medium. Yet, it remains unclear how feedback, through its connection to key galaxy properties, shapes the radial gas density profile in the host halo. We tackle this question using suites of the EAGLE, IllustrisTNG, and Simba cosmological hydrodynamical simulations, which span a variety of feedback models. We develop a random forest algorithm that predicts the radial gas density profile within haloes from the total halo mass and five global properties of the central galaxy: gas and stellar mass; star formation rate; mass and accretion rate of the central black hole (BH). The algorithm reproduces the simulated gas density profiles with an average accuracy of ∼80-90% over the halo mass range 10^{9.5} \, \mathrm{M}_{\odot} < M_{\rm 200c} < 10^{15} \, \mathrm{M}_{\odot} and redshift interval $0
09 Dec 2025
A lightweight framework, RAGLens, accurately identifies and explains faithfulness issues in Retrieval-Augmented Generation outputs by leveraging Sparse Autoencoders on LLM internal states. This approach achieves over 80% AUC on RAG benchmarks and provides interpretable, token-level feedback for effective hallucination mitigation.
Reward-model-based fine-tuning is a central paradigm in aligning Large Language Models with human preferences. However, such approaches critically rely on the assumption that proxy reward models accurately reflect intended supervision, a condition often violated due to annotation noise, bias, or limited coverage. This misalignment can lead to undesirable behaviors, where models optimize for flawed signals rather than true human values. In this paper, we investigate a novel framework to identify and mitigate such misalignment by treating the fine-tuning process as a form of knowledge integration. We focus on detecting instances of proxy-policy conflicts, cases where the base model strongly disagrees with the proxy. We argue that such conflicts often signify areas of shared ignorance, where neither the policy nor the reward model possesses sufficient knowledge, making them especially susceptible to misalignment. To this end, we propose two complementary metrics for identifying these conflicts: a localized Proxy-Policy Alignment Conflict Score (PACS) and a global Kendall-Tau Distance measure. Building on this insight, we design an algorithm named Selective Human-in-the-loop Feedback via Conflict-Aware Sampling (SHF-CAS) that targets high-conflict QA pairs for additional feedback, refining both the reward model and policy efficiently. Experiments on two alignment tasks demonstrate that our approach enhances general alignment performance, even when trained with a biased proxy reward. Our work provides a new lens for interpreting alignment failures and offers a principled pathway for targeted refinement in LLM training.
Recent advances in diffusion-based generative models have achieved remarkable visual fidelity, yet a detailed understanding of how specific perceptual attributes - such as color and shape - are internally represented remains limited. This work explores how color is encoded in a generative model through a systematic analysis of the latent representations in Stable Diffusion. Through controlled synthetic datasets, principal component analysis (PCA) and similarity metrics, we reveal that color information is encoded along circular, opponent axes predominantly captured in latent channels c_3 and c_4, whereas intensity and shape are primarily represented in channels c_1 and c_2. Our findings indicate that the latent space of Stable Diffusion exhibits an interpretable structure aligned with a efficient coding representation. These insights provide a foundation for future work in model understanding, editing applications, and the design of more disentangled generative frameworks.
08 Dec 2025
Luxembourg Institute of Science and TechnologyHo Chi Minh City University of TechnologyTeesside UniversityHo Chi Minh City University of Technology (HCMUT)Ho Chi Minh City University of ScienceVietnam National University - Ho Chi Minh CityHo Chi Minh City University of Science (HCMUS)Vietnam National University - Ho Chi Minh City (VNU-HCM)
As Large Language Models (LLMs) increasingly operate as autonomous decision-makers in interactive and multi-agent systems and human societies, understanding their strategic behaviour has profound implications for safety, coordination, and the design of AI-driven social and economic infrastructures. Assessing such behaviour requires methods that capture not only what LLMs output, but the underlying intentions that guide their decisions. In this work, we extend the FAIRGAME framework to systematically evaluate LLM behaviour in repeated social dilemmas through two complementary advances: a payoff-scaled Prisoners Dilemma isolating sensitivity to incentive magnitude, and an integrated multi-agent Public Goods Game with dynamic payoffs and multi-agent histories. These environments reveal consistent behavioural signatures across models and languages, including incentive-sensitive cooperation, cross-linguistic divergence and end-game alignment toward defection. To interpret these patterns, we train traditional supervised classification models on canonical repeated-game strategies and apply them to FAIRGAME trajectories, showing that LLMs exhibit systematic, model- and language-dependent behavioural intentions, with linguistic framing at times exerting effects as strong as architectural differences. Together, these findings provide a unified methodological foundation for auditing LLMs as strategic agents and reveal systematic cooperation biases with direct implications for AI governance, collective decision-making, and the design of safe multi-agent systems.
Although Multimodal Large Language Models (MLLMs) have advanced substantially, they remain vulnerable to object hallucination caused by language priors and visual information loss. To address this, we propose SAVE (Sparse Autoencoder-Driven Visual Information Enhancement), a framework that mitigates hallucination by steering the model along Sparse Autoencoder (SAE) latent features. A binary object-presence question-answering probe identifies the SAE features most indicative of the model's visual information processing, referred to as visual understanding features. Steering the model along these identified features reinforces grounded visual understanding and effectively reduces hallucination. With its simple design, SAVE outperforms state-of-the-art training-free methods on standard benchmarks, achieving a 10\%p improvement in CHAIR\_S and consistent gains on POPE and MMHal-Bench. Extensive evaluations across multiple models and layers confirm the robustness and generalizability of our approach. Further analysis reveals that steering along visual understanding features suppresses the generation of uncertain object tokens and increases attention to image tokens, mitigating hallucination. Code is released at this https URL.
Textual explanations make image classifier decisions transparent by describing the prediction rationale in natural language. Large vision-language models can generate captions but are designed for general visual understanding, not classifier-specific reasoning. Existing zero-shot explanation methods align global image features with language, producing descriptions of what is visible rather than what drives the prediction. We propose TEXTER, which overcomes this limitation by isolating decision-critical features before alignment. TEXTER identifies the neurons contributing to the prediction and emphasizes the features encoded in those neurons -- i.e., the decision-critical features. It then maps these emphasized features into the CLIP feature space to retrieve textual explanations that reflect the model's reasoning. A sparse autoencoder further improves interpretability, particularly for Transformer architectures. Extensive experiments show that TEXTER generates more faithful and interpretable explanations than existing methods. The code will be publicly released.
We investigate the short-context dominance hypothesis: that for most sequences, a small local prefix suffices to predict their next tokens. Using large language models as statistical oracles, we measure the minimum context length (MCL) needed to reproduce accurate full-context predictions across datasets with sequences of varying lengths. For sequences with 1-7k tokens from long-context documents, we consistently find that 75-80% require only the last 96 tokens at most. Given the dominance of short-context tokens, we then ask whether it is possible to detect challenging long-context sequences for which a short local prefix does not suffice for prediction. We introduce a practical proxy to MCL, called Distributionally Aware MCL (DaMCL), that does not require knowledge of the actual next-token and is compatible with sampling strategies beyond greedy decoding. Our experiments validate that simple thresholding of the metric defining DaMCL achieves high performance in detecting long vs. short context sequences. Finally, to counter the bias that short-context dominance induces in LLM output distributions, we develop an intuitive decoding algorithm that leverages our detector to identify and boost tokens that are long-range-relevant. Across Q&A tasks and model architectures, we confirm that mitigating the bias improves performance.
We study the expressivity of one-dimensional (1D) ReLU deep neural networks through the lens of their linear regions. For randomly initialized, fully connected 1D ReLU networks (He scaling with nonzero bias) in the infinite-width limit, we prove that the expected number of linear regions grows as ∑i=1Lni+o(∑i=1Lni)+1, where nℓ denotes the number of neurons in the ℓ-th hidden layer. We also propose a function-adaptive notion of sparsity that compares the expected regions used by the network to the minimal number needed to approximate a target within a fixed tolerance.
Concept Bottleneck Models (CBMs) provide a basis for semantic abstractions within a neural network architecture. Such models have primarily been seen through the lens of interpretability so far, wherein they offer transparency by inferring predictions as a linear combination of semantic concepts. However, a linear combination is inherently limiting. So we propose the enhancement of concept-based learning models through propositional logic. We introduce a logic module that is carefully designed to connect the learned concepts from CBMs through differentiable logic operations, such that our proposed LogicCBM can go beyond simple weighted combinations of concepts to leverage various logical operations to yield the final predictions, while maintaining end-to-end learnability. Composing concepts using a set of logic operators enables the model to capture inter-concept relations, while simultaneously improving the expressivity of the model in terms of logic operations. Our empirical studies on well-known benchmarks and synthetic datasets demonstrate that these models have better accuracy, perform effective interventions and are highly interpretable.
Recent advances in Image Quality Assessment (IQA) have leveraged Multi-modal Large Language Models (MLLMs) to generate descriptive explanations. However, despite their strong visual perception modules, these models often fail to reliably detect basic low-level distortions such as blur, noise, and compression, and may produce inconsistent evaluations across repeated inferences. This raises an essential question: do MLLM-based IQA systems truly perceive the visual features that matter? To examine this issue, we introduce a low-level distortion perception task that requires models to classify specific distortion types. Our component-wise analysis shows that although MLLMs are structurally capable of representing such distortions, they tend to overfit training templates, leading to biases in quality scoring. As a result, critical low-level features are weakened or lost during the vision-language alignment transfer stage. Furthermore, by computing the semantic distance between visual features and corresponding semantic tokens before and after component-wise fine-tuning, we show that improving the alignment of the vision encoder dramatically enhances distortion recognition accuracy, increasing it from 14.92% to 84.43%. Overall, these findings indicate that incorporating dedicated constraints on the vision encoder can strengthen text-explainable visual representations and enable MLLM-based pipelines to produce more coherent and interpretable reasoning in vision-centric tasks.
A framework named Self-Refining Diffusion from Kookmin University utilizes Explainable AI-based Flaw Activation Maps to enable diffusion models to self-correct visual artifacts in generated images, achieving up to a 27.3% FID reduction on datasets like Oxford 102 Flower. The method redefines XAI's role from passive diagnosis to active guidance for performance enhancement in generative models.
Craig interpolation and uniform interpolation have many applications in knowledge representation, including explainability, forgetting, modularization and reuse, and even learning. At the same time, many relevant knowledge representation formalisms do in general not have Craig or uniform interpolation, and computing interpolants in practice is challenging. We have a closer look at two prominent knowledge representation formalisms, description logics and logic programming, and discuss theoretical results and practical methods for computing interpolants.
We propose ϕ-test, a global feature-selection and significance procedure for black-box predictors that combines Shapley attributions with selective inference. Given a trained model and an evaluation dataset, ϕ-test performs SHAP-guided screening and fits a linear surrogate on the screened features via a selection rule with a tractable selective-inference form. For each retained feature, it outputs a Shapley-based global score, a surrogate coefficient, and post-selection p-values and confidence intervals in a global feature-importance table. Experiments on real tabular regression tasks with tree-based and neural backbones suggest that ϕ-test can retain much of the predictive ability of the original model while using only a few features and producing feature sets that remain fairly stable across resamples and backbone classes. In these settings, ϕ-test acts as a practical global explanation layer linking Shapley-based importance summaries with classical statistical inference.
There are no more papers matching your filters at the moment.