Joint Quantum Institute
27 Nov 2024
Toric t-designs, or equivalently t-designs on the diagonal subgroup of the unitary group, are sets of points on the torus over which sums reproduce integrals of degree t monomials over the full torus. Motivated by the projective structure of quantum mechanics, we develop the notion of t-designs on the projective torus, which have a much more restricted structure than their counterparts on full tori. We provide various new constructions of toric and projective toric designs and prove bounds on their size. We draw connections between projective toric designs and a diverse set of mathematical objects, including difference and Sidon sets from the field of additive combinatorics, symmetric, informationally complete positive operator valued measures and complete sets of mutually unbiased bases (MUBs) from quantum information theory, and crystal ball sequences of certain root lattices. Using these connections, we prove bounds on the maximal size of dense Btmodm sets. We also use projective toric designs to construct families of quantum state designs. In particular, we construct families of (uniformly-weighted) quantum state 2-designs in dimension d of size exactly d(d+1) that do not form complete sets of MUBs, thereby disproving a conjecture concerning the relationship between designs and MUBs (Zhu 2015). We then propose a modification of Zhu's conjecture and discuss potential paths towards proving this conjecture. We prove a fundamental distinction between complete sets of MUBs in prime-power dimensions versus in dimension 6 (and, we conjecture, in all non-prime-power dimensions), the distinction relating to group structure of the corresponding projective toric design. Finally, we discuss many open questions about the properties of these projective toric designs and how they relate to other questions in number theory, geometry, and quantum information.
This research details the experimental realization of pure gyration in an on-chip superconducting microwave device, utilizing spatio-temporal modulation of resonator frequencies. The study demonstrates the first fully on-chip superconducting gyrator, achieving precisely pi phase contrast with near-zero magnitude contrast at microwave frequencies, a crucial step for integrated quantum circuits.
We use Pauli Path simulation to variationally obtain parametrized circuits for preparing ground states of various quantum many-body Hamiltonians. These include the quantum Ising model in one dimension, in two dimensions on square and heavy-hex lattices, and the Kitaev honeycomb model, all at system sizes of one hundred qubits or more, beyond the reach of exact state-vector simulation, thereby reaching utility scale. We benchmark the Pauli Path simulation results against exact ground-state energies when available, and against density-matrix renormalization group calculations otherwise, finding strong agreement. To further assess the quality of the variational states, we evaluate the magnetization in the x and z directions for the quantum Ising models and compute the topological entanglement entropy for the Kitaev honeycomb model. Finally, we prepare approximate ground states of the Kitaev honeycomb model with 48 qubits, in both the gapped and gapless regimes, on Quantinuum's System Model H2 quantum computer using parametrized circuits obtained from Pauli Path simulation. We achieve a relative energy error of approximately 5% without error mitigation and demonstrate the braiding of Abelian anyons on the quantum device beyond fixed-point models.
02 Oct 2025
We present a sample- and time-efficient algorithm to learn any bosonic Fock state acted upon by an arbitrary Gaussian unitary. As a special case, this algorithm efficiently learns states produced in Fock state BosonSampling, thus resolving an open question put forth by Aaronson and Grewal (Aaronson, Grewal 2023). We further study a hierarchy of classes of states beyond Gaussian states that are specified by a finite number of their higher moments. Using the higher moments, we find a full spectrum of invariants under Gaussian unitaries, thereby providing necessary conditions for two states to be related by an arbitrary (including active, e.g. beyond linear optics) Gaussian unitary.
09 Jan 2025
Researchers from QuICS and other institutions propose a bilayer architecture and teleportation-based routing to implement high-rate quantum LDPC codes on 2D local gate platforms. This approach reduces physical qubit overhead compared to surface codes while maintaining comparable logical error rates, leveraging partial syndrome measurement to mitigate circuit depth.
14 Oct 2025
We study measurement-induced entanglement generated by column-by-column sampling of noisy 2D random Clifford circuits of size N and depth T. Focusing on the operator entanglement Sop of the sampling-induced boundary state, first, we reproduce in the noiseless limit a finite-depth transition from area- to volume-law scaling. With on-site probablistic trace noise at any constant rate p>0, the maximal Sop attained along the sampling trajectory obeys an area law in the boundary length and scales approximately linearly with T/p. By analyzing the spatial distribution of stabilizer generators, we observe exponential localization of stabilizer generators; this both accounts for the scaling of the maximal Sop and implies an exponential decay of conditional mutual information across buffered tripartitions, which we also confirm numerically. Together, these results indicate that constant local noise destroys long-range, volume-law measurement-induced entanglement in 2D random Clifford circuits. Finally, based on the observed scaling, we conjecture that a tensor-network-based algorithm can efficiently sample from noisy 2D random Clifford circuits (i) at sub-logarithmic depths T=o(logN) for any constant noise rate p=Ω(1), and (ii) at constant depths T=O(1) for noise rates p=Ω(log−1N).
Finite-temperature phases of many-body quantum systems are fundamental to
phenomena ranging from condensed-matter physics to cosmology, yet they are
generally difficult to simulate. Using an ion trap quantum computer and
protocols motivated by the Quantum Approximate Optimization Algorithm (QAOA),
we generate nontrivial thermal quantum states of the transverse-field Ising
model (TFIM) by preparing thermofield double states at a variety of
temperatures. We also prepare the critical state of the TFIM at zero
temperature using quantum-classical hybrid optimization. The entanglement
structure of thermofield double and critical states plays a key role in the
study of black holes, and our work simulates such nontrivial structures on a
quantum computer. Moreover, we find that the variational quantum circuits
exhibit noise thresholds above which the lowest depth QAOA circuits provide the
best results.
Simulating out-of-equilibrium dynamics of quantum field theories in nature is challenging with classical methods, but is a promising application for quantum computers. Unfortunately, simulating interacting bosonic fields involves a high boson-to-qubit encoding overhead. Furthermore, when mapping to qubits, the infinite-dimensional Hilbert space of bosons is necessarily truncated, with truncation errors that grow with energy and time. A qubit-based quantum computer, augmented with an active bosonic register, and with qubit, bosonic, and mixed qubit-boson quantum gates, offers a more powerful platform for simulating bosonic theories. We demonstrate this capability experimentally in a hybrid analog-digital trapped-ion quantum computer, where qubits are encoded in the internal states of the ions, and the bosons in the ions' motional states. Specifically, we simulate nonequilibrium dynamics of a (1+1)-dimensional Yukawa model, a simplified model of interacting nucleons and pions, and measure fermion- and boson-occupation-state probabilities. These dynamics populate high bosonic-field excitations starting from an empty state, and the experimental results capture well such high-occupation states. This simulation approaches the regime where classical methods become challenging, bypasses the need for a large qubit overhead, and removes truncation errors. Our results, therefore, open the way to achieving demonstrable quantum advantage in qubit-boson quantum computing.
02 Dec 2025
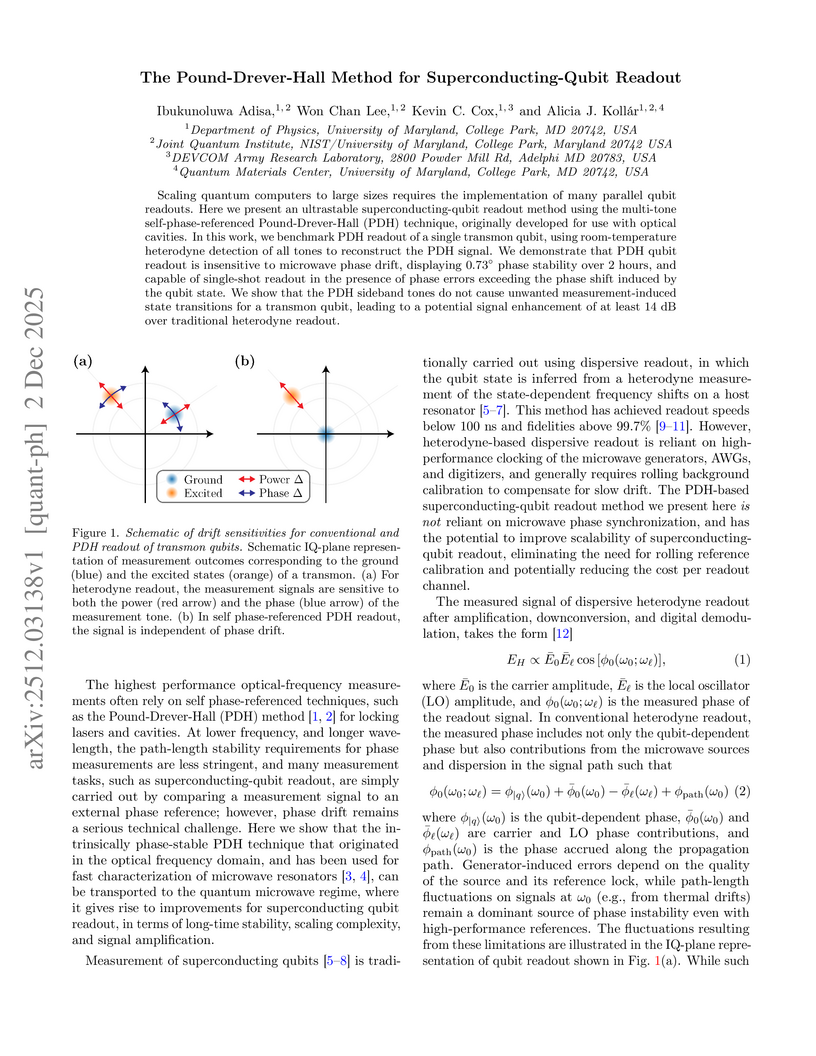
Researchers demonstrate the Pound-Drever-Hall (PDH) method for superconducting-qubit readout, achieving an RMS phase noise of 0.73° over 2 hours, a substantial improvement over the ~400° drift seen in conventional heterodyne methods. This approach also offers a potential 14 dB signal enhancement without inducing measurement-induced state transitions.
We investigate the stability of electron-hole superfluidity in two-dimensional bilayers with unequal and anisotropic effective masses. Using a zero-temperature, self-consistent Hartree-Fock approach, we study two experimentally relevant deviations from the ideal equal-mass isotropic case: (i) isotropic but unequal conduction and valence band masses (mc∗=mv∗), and (ii) equal average masses with orthogonal in-plane anisotropies (mc,x∗,mc,y∗)=(m1∗,m2∗) and (mv,x∗,mv,y∗)=(m2∗,m1∗). For both scenarios, we compute the order parameter and analyze the BEC-BCS crossover as a function of layer separation and mass ratio. We find that both mass imbalance and mass anisotropy reduce the pairing strength and suppress the inferred critical temperature Tc by breaking perfect Fermi surface nesting, and shift the BEC-BCS crossover. Despite these effects, superfluidity remains robust across the full range of densities and interlayer separations considered, with no transition to an unpaired plasma state in the absence of screening. Our results provide a baseline for understanding the interplay of mass mismatch and anisotropy in current and emerging bilayer platforms, including van der Waals heterostructures and anisotropic two-dimensional semiconductors. Our work also establishes that Fermi surface nesting is not a key ingredient for the bilayer superfluidity, which is always the ground state for all electron-hole bilayers although the resultant Tc depends on the parameter details and may very well be unmeasurably low for large interlayer separations.
22 Oct 2025
We extend the previous study of extracting crystalline symmetry-protected topological invariants to the correlated regime. We construct the interacting Hofstadter model defined on square lattice with the rotation and translation symmetry defects: disclination and dislocation. The model realizes Chern insulator and the charge density wave state as one tunes interactions. Employing the density matrix renormalization group (DMRG) method, we calculate the excess charge around the defects and find that the topological invariants remain quantized in both phases, with the topological quantity extracted to great precision. This study paves the way for utilizing matrix product state, and potentially other quantum many-body computation methods, to efficiently study crystalline symmetry defects on 2D interacting lattice systems.
09 Feb 2015
We engineered a two-dimensional magnetic lattice in an elongated strip geometry, with effective per-plaquette flux ~4/3 times the flux quanta. We imaged the localized edge and bulk states of atomic Bose-Einstein condensates in this strip, with single lattice-site resolution along the narrow direction. Further, we observed both the skipping orbits of excited atoms traveling down our system's edges, analogues to edge magnetoplasmons in 2-D electron systems, and a dynamical Hall effect for bulk excitations. Our lattice's long direction consisted of the sites of an optical lattice and its narrow direction consisted of the internal atomic spin states. Our technique has minimal heating, a feature that will be important for spectroscopic measurements of the Hofstadter butterfly and realizations of Laughlin's charge pump.
25 Aug 2025
A central goal in quantum error correction is to reduce the overhead of fault-tolerant quantum computing by increasing noise thresholds and reducing the number of physical qubits required to sustain a logical qubit. We introduce a potential path towards this goal based on a family of dynamically generated quantum error correcting codes that we call "hyperbolic Floquet codes.'' These codes are defined by a specific sequence of non-commuting two-body measurements arranged periodically in time that stabilize a topological code on a hyperbolic manifold with negative curvature. We focus on a family of lattices for n qubits that, according to our prescription that defines the code, provably achieve a finite encoding rate (1/8+2/n) while still requiring only two-body measurements. Similar to hyperbolic surface codes, the distance of the code at each time-step scales at most logarithmically in n. The family of lattices we choose indicates that this scaling is achievable in practice. We develop and benchmark an efficient matching-based decoder that provides evidence of a threshold near 0.1% in a phenomenological noise model and 0.25% in an entangling measurements noise model. Utilizing weight-two check operators and a qubit connectivity of 3, one of our hyperbolic Floquet codes uses 400 physical qubits to encode 52 logical qubits with a code distance of 8, i.e., it is a [[400,52,8]] code. At small error rates, comparable logical error suppression to this code requires 5x as many physical qubits (1924) when using the honeycomb Floquet code with the same noise model and decoder.
13 Jul 2010
We consider two-dimensional non-centrosymmetric superconductors, where the order parameter is a mixture of s-wave and p-wave parts, in the presence of an externally induced Zeeman splitting. We derive the conditions under which the system is in a non-Abelian phase. By considering the non-degenerate zero-energy Majorana solutions of the Bogoliubov-de Gennes (BdG) equations for a vortex and by constructing a topological invariant, we show that the condition for the non-Abelian phase to exist is completely independent of the triplet pairing amplitude. The existence condition for the non-Abelian phase derived from the real space solutions of the BdG equations involves the Pfaffian of the BdG Hamiltonian at k = 0, which is completely insensitive to the magnitude of the p-wave component of the order parameter. We arrive at the same conclusion by using the appropriate topological invariant for this case. This is in striking contrast to the analogous condition for the time-reversal invariant topological phases, in which the amplitude of the p-wave component must be larger than the amplitude of the s-wave piece of the order parameter. As a by-product, we establish the intrinsic connection between the Pfaffian of the BdG Hamiltonian at k = 0 (which arises at the BdG approach) and the relevant Z topological invariant.
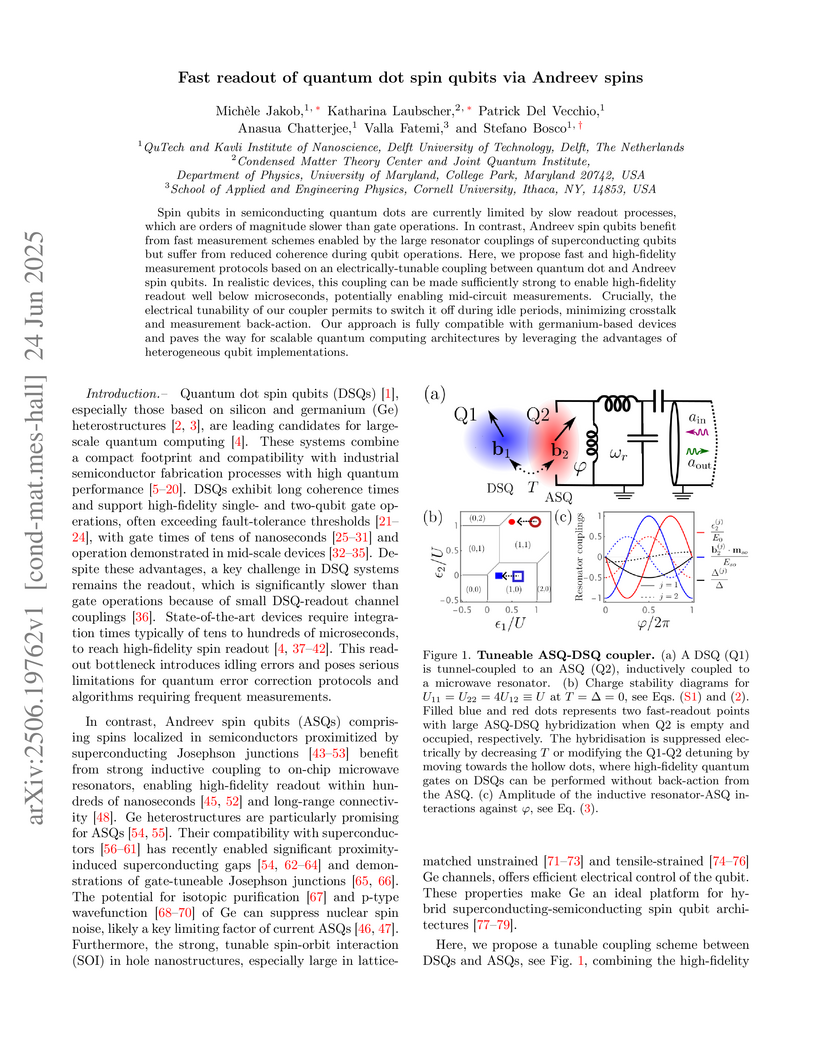
Spin qubits in semiconducting quantum dots are currently limited by slow readout processes, which are orders of magnitude slower than gate operations. In contrast, Andreev spin qubits benefit from fast measurement schemes enabled by the large resonator couplings of superconducting qubits but suffer from reduced coherence during qubit operations. Here, we propose fast and high-fidelity measurement protocols based on an electrically-tunable coupling between quantum dot and Andreev spin qubits. In realistic devices, this coupling can be made sufficiently strong to enable high-fidelity readout well below microseconds, potentially enabling mid-circuit measurements. Crucially, the electrical tunability of our coupler permits to switch it off during idle periods, minimizing crosstalk and measurement back-action. Our approach is fully compatible with germanium-based devices and paves the way for scalable quantum computing architectures by leveraging the advantages of heterogeneous qubit implementations.
We implement a quantum generalization of a neural network on trapped-ion and IBM superconducting quantum computers to classify MNIST images, a common benchmark in computer vision. The network feedforward involves qubit rotations whose angles depend on the results of measurements in the previous layer. The network is trained via simulation, but inference is performed experimentally on quantum hardware. The classical-to-quantum correspondence is controlled by an interpolation parameter, a, which is zero in the classical limit. Increasing a introduces quantum uncertainty into the measurements, which is shown to improve network performance at moderate values of the interpolation parameter. We then focus on particular images that fail to be classified by a classical neural network but are detected correctly in the quantum network. For such borderline cases, we observe strong deviations from the simulated behavior. We attribute this to physical noise, which causes the output to fluctuate between nearby minima of the classification energy landscape. Such strong sensitivity to physical noise is absent for clear images. We further benchmark physical noise by inserting additional single-qubit and two-qubit gate pairs into the neural network circuits. Our work provides a springboard toward more complex quantum neural networks on current devices: while the approach is rooted in standard classical machine learning, scaling up such networks may prove classically non-simulable and could offer a route to near-term quantum advantage.
13 Sep 2025
Universality and scaling laws are hallmarks of equilibrium phase transitions and critical phenomena. However, extending these concepts to non-equilibrium systems is an outstanding challenge. Despite recent progress in the study of dynamical phases, the universality classes and scaling laws for non-equilibrium phenomena are far less understood than those in equilibrium. In this work, using a trapped-ion quantum simulator with single-spin resolution, we investigate the non-equilibrium nature of critical fluctuations following a quantum quench to the critical point. We probe the scaling of spin fluctuations after a series of quenches to the critical Hamiltonian of a long-range Ising model. With systems of up to 50 spins, we show that the amplitude and timescale of the post-quench fluctuations scale with system size with distinct universal critical exponents, depending on the quench protocol. While a generic quench can lead to thermal critical behavior, we find that a second quench from one critical state to another (i.e.~a double quench) results in a new universal non-equilibrium behavior, identified by a set of critical exponents distinct from their equilibrium counterparts. Our results demonstrate the ability of quantum simulators to explore universal scaling beyond equilibrium.
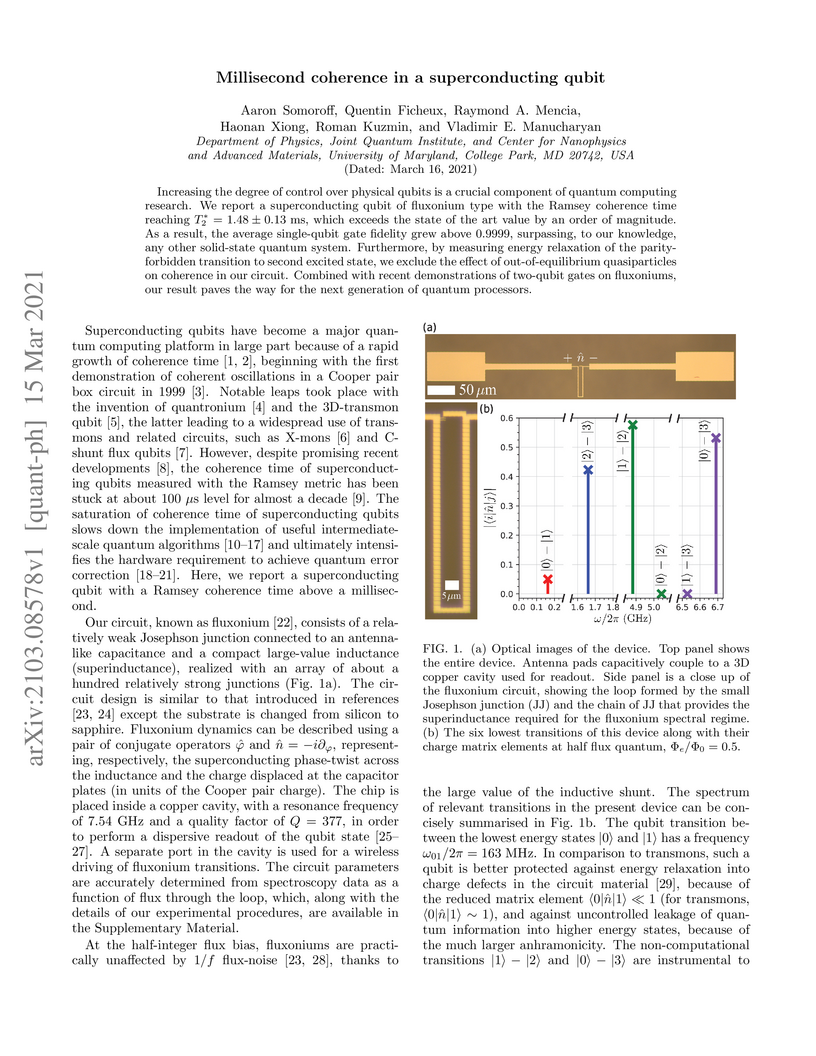
Increasing the degree of control over physical qubits is a crucial component of quantum computing research. We report a superconducting qubit of fluxonium type with the Ramsey coherence time reaching T2∗=1.48±0.13 ms, which exceeds the state of the art value by an order of magnitude. As a result, the average single-qubit gate fidelity grew above 0.9999, surpassing, to our knowledge, any other solid-state quantum system. Furthermore, by measuring energy relaxation of the parity-forbidden transition to second excited state, we exclude the effect of out-of-equilibrium quasiparticles on coherence in our circuit. Combined with recent demonstrations of two-qubit gates on fluxoniums, our result paves the way for the next generation of quantum processors.
30 Aug 2024
We report the 2022 self-consistent values of constants and conversion factors of physics and chemistry recommended by the Committee on Data of the International Science Council (CODATA). The recommended values can also be found at this http URL. The values are based on a least-squares adjustment that takes into account all theoretical and experimental data available through 31 December 2022. A discussion of the major improvements as well as inconsistencies within the data is given.
25 Oct 2018
We report superconducting fluxonium qubits with coherence times largely
limited by energy relaxation and reproducibly satisfying T2 > 100 microseconds
(T2 > 300 microseconds in one device). Moreover, given the state of the art
values of the surface loss tangent and the 1/f flux noise amplitude, coherence
can be further improved beyond 1 millisecond. Our results violate a common
viewpoint that the number of Josephson junctions in a superconducting circuit
-- over 100 here -- must be minimized for best qubit coherence. We outline how
the unique to fluxonium combination of long coherence time and large
anharmonicity can benefit both gate-based and adiabatic quantum computing.
There are no more papers matching your filters at the moment.