The driving forces of chiral active particles and deformations of cells are often modeled by spatially inhomogeneous but temporally periodic driving forces. Such inhomogeneous oscillatory driving forces have only recently been proposed in the context of active matter, and their effects on the systems are not yet fully understood. In this work, we theoretically study the impact of spatially inhomogeneous oscillatory driving forces on continuous symmetry breaking. We first analyze the linear model for the soft modes in the ordered phase to derive the lower critical dimension of the model, and then analyze the spherical model to investigate more detailed phase behaviors. Interestingly, our analysis reveals that symmetry breaking occurs even in one and two dimensions, where the Hohenberg--Mermin--Wagner theorem prohibits continuous symmetry breaking in equilibrium. Furthermore, fluctuations of conserved quantities, such as density, are anomalously suppressed in the long-wavelength, {\it i.e.}, show hyperuniformity.

We study an attractive Hubbard model on bipartite lattices. In the grand canonical formalism,we prove the existence of superconducting long-range order in the ground state with the chemical potential corresponding to half filling. We also study the low-energy excitations above several ground states for the translationally invariant Hamiltonian. We prove the following: (i) The pairing excitations are gapless above the ground states when the number of fermions deviates from that of the half filling by the order of the volume. (ii) A certain class of single-fermion excitations shows a non-vanishing spectral gap above the ground state with an even number of fermions in a strong coupling and low-density regime.

The uncertainty principle guarantees a non-zero value for the positional uncertainty, $\left\langle\Delta x^2\right\rangle > 0$, even without thermal fluctuations. This implies that quantum fluctuations inherently enhance positional uncertainty at zero temperature. A natural question then arises: what happens at finite temperatures, where the interplay between quantum and thermal fluctuations may give rise to complex and intriguing behaviors? To address this question, we systematically investigate the positional uncertainty, $\left\langle\Delta x^2\right\rangle$, of a particle in equilibrium confined within a nonlinear potential of the form $V(x) \propto x^a$, where$a = 2, 4, 6, \dots$ represents an even exponent. Using path integral Monte Carlo simulations, we calculate $\left\langle\Delta x^2\right\rangle$ in equilibrium as a function of the thermal de Broglie wavelength $\Lambda$. Interestingly, for large values of $a$, $\left\langle\Delta x^2\right\rangle$ exhibits a non-monotonic dependence on $\Lambda$: it initially decreases with increasing $\Lambda$ at small $\Lambda$ but increases at larger $\Lambda$. To further understand this behavior, we employ a semiclassical approximation, which reveals that quantum fluctuations can reduce positional uncertainty for small $\Lambda$ when the nonlinearity of the potential is sufficiently strong. Finally, we discuss the potential implications of this result for many-body phenomena driven by strong nonlinear interactions, such as glass transitions, where the transition densities exhibit a similar non-monotonic dependence on $\Lambda$.

Transformers exhibit in-context learning (ICL): the ability to use novel information presented in the context without additional weight updates. Recent work shows that ICL emerges when models are trained on a sufficiently diverse set of tasks and the transition from memorization to generalization is sharp with increasing task diversity. One interpretation is that a network's limited capacity to memorize favors generalization. Here, we examine the mechanistic underpinnings of this transition using a small transformer applied to a synthetic ICL task. Using theory and experiment, we show that the sub-circuits that memorize and generalize can be viewed as largely independent. The relative rates at which these sub-circuits learn explains the transition from memorization to generalization, rather than capacity constraints. We uncover a memorization scaling law, which determines the task diversity threshold at which the network generalizes. The theory quantitatively explains a variety of other ICL-related phenomena, including the long-tailed distribution of when ICL is acquired, the bimodal behavior of solutions close to the task diversity threshold, the influence of contextual and data distributional statistics on ICL, and the transient nature of ICL.

We review the Lieb-Schultz-Mattis theorem and its variants, which are no-go theorems that state that a quantum many-body system with certain conditions cannot have a locally-unique gapped ground state. We restrict ourselves to one-dimensional quantum spin systems and discuss both the generalized Lieb-Schultz-Mattis theorem for models with U(1) symmetry and the extended Lieb-Schultz-Mattis theorem for models with discrete symmetry. We also discuss the implication of the same arguments to systems on the infinite cylinder, both with the periodic boundary conditions and with the spiral boundary conditions. For models with U(1) symmetry, we here present a rearranged version of the original proof of Lieb, Schultz, and Mattis based on the twist operator. As the title suggests we take a modern topological point of view and prove the generalized Lieb-Schultz-Mattis theorem by making use of a topological index (which coincides with the filling factor). By a topological index, we mean an index that characterizes a locally-unique gapped ground state and is invariant under continuous (or smooth) modification of the ground state. For models with discrete symmetry, we describe the basic idea of the most general proof based on the topological index introduced in the context of symmetry-protected topological phases. We start from background materials such as the classification of projective representations of the symmetry group. We also review the notion that we call a locally-unique gapped ground state of a quantum spin system on an infinite lattice and present basic theorems. This notion turns out to be natural and useful from the physicists' point of view. We have tried to make the present article readable and almost self-contained. We only assume basic knowledge about quantum spin systems.

We study the critical behavior of the $O(n)$ model under steady shear flow using a dynamical renormalization group (RG) method. Incorporating the strong anisotropy in scaling ansatz, which has been neglected in earlier RG analyses, we identify a new stable Gaussian fixed point. This fixed point reproduces the anisotropic scaling of static and dynamical critical exponents for both non-conserved (Model A) and conserved (Model B) order parameters. Notably, the upper critical dimensions are $d_{\text{up}} = 2$ for the non-conserved order parameter (Model A) and $d_{\text{up}} = 0$ for the conserved order parameter (Model B), implying that the mean-field critical exponents are observed even in both $d=2$ and $3$ dimensions. Furthermore, the scaling exponent of the order parameter is negative for all dimensions $d \geq 2$, indicating that shear flow stabilizes the long-range order associated with continuous symmetry breaking even in $d = 2$. In other words, the lower critical dimensions are d_{\rm low} < 2 for both types of order parameters. This contrasts with equilibrium systems, where the Hohenberg -- Mermin -- Wagner theorem prohibits continuous symmetry breaking in $d = 2$.

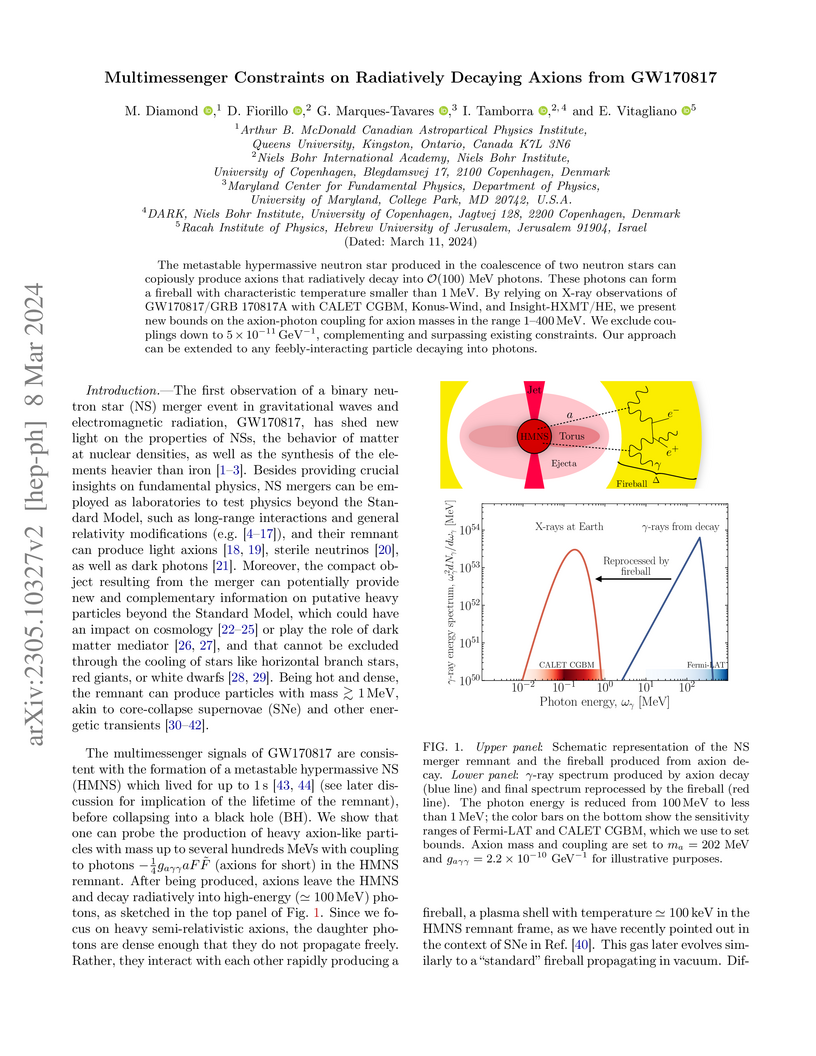
The metastable hypermassive neutron star produced in the coalescence of two neutron stars can copiously produce axions that radiatively decay into $\mathcal{O}(100)$~MeV photons. These photons can form a fireball with characteristic temperature smaller than $1\rm\, MeV$. By relying on X-ray observations of GW170817/GRB 170817A with CALET CGBM, Konus-Wind, and Insight-HXMT/HE, we present new bounds on the axion-photon coupling for axion masses in the range $1$-$400\,\rm MeV$. We exclude couplings down to $5\times 10^{-11}\,\rm GeV^{-1}$, complementing and surpassing existing constraints. Our approach can be extended to any feebly-interacting particle decaying into photons.

Causal additive models provide a tractable yet expressive framework for causal discovery in the presence of hidden variables. However, when unobserved backdoor or causal paths exist between two variables, their causal relationship is often unidentifiable under existing theories. We establish sufficient conditions under which causal directions can be identified in many such cases. In particular, we derive conditions that enable identification of the parent-child relationship in a bow, an adjacent pair of observed variables sharing a hidden common parent. This represents a notoriously difficult case in causal discovery, and, to our knowledge, no prior work has established such identifiability in any causal model without imposing assumptions on the hidden variables. Our conditions rely on new characterizations of regression sets and a hybrid approach that combines independence among regression residuals with conditional independencies among observed variables. We further provide a sound and complete algorithm that incorporates these insights, and empirical evaluations demonstrate competitive performance with state-of-the-art methods.

We study the $S=\frac{1}{2}$ quantum spin system on the $d$-dimensional hypercubic lattice with $d\ge2$ with uniform nearest-neighbor interaction of the XY or XYZ type and arbitrary uniform magnetic field. By extending the method recently developed for quantum spin chains, we prove that the model possesses no local conserved quantities except for the trivial ones, such as the Hamiltonian. This result strongly suggests that the model is non-integrable. We note that our result applies to the XX model without a magnetic field, which is one of the easiest solvable models in one dimension.

We compute the Azumaya loci of Kauffman-bracket skein algebras of closed surfaces at odd roots of unity and provide partial results for open surfaces as well. As applications, we give an alternative definition of the projective representations of the Torelli groups derived from non-semisimple TQFTs and we strengthen a result by Frohman-Kania Bartoszynska-Lê about the dimensions of some quotients of the skein modules of closed 3-manifolds.

The density matrix renormalization group (DMRG) is a celebrated tensor network algorithm, which computes the ground states of one-dimensional quantum many-body systems very efficiently. Here we propose an improved formulation of continuous tensor network algorithms, which we name a matrix product renormalization group (MPRG). MPRG is a universal quantum many-body solver, which potentially works at both zero and finite temperatures, in two and higher dimensions, and is even applicable to open quantum systems. Furthermore, MPRG does not rely on any variational principles and thus supports any kind of non-Hermitian systems in any dimension. As a demonstration, we present critical properties of the Yang-Lee edge singularity in one dimension as a representative non-Hermitian system.

Fractional excitations provide a key to identifying sought-after topological quantum spin liquid states in realistic materials. Their single-particle dynamics already presents a challenging many-body problem on account of the coupling to their emergent gauge field. Here, we study the spinon excitations of kagome ice, realized at the $2/3$ magnetization plateau of spin ice, by combining up-to-$63$-site exact diagonalization with an analytical state graph mapping. We find a macroscopically degenerate mode in the spinon spectrum. It originates from the destructive interference due to the interaction with surrounding gauge fields, a form of many-body caging. We explicitly construct, and count, the concomitant many-body wave functions. Finally, we discuss the possible role of these flat modes in the magnetization process of kagome antiferromagnets, in particular with regard to the asymmetric termination of the kagome ice magnetisation plateau.

In this work, we discuss how the linear and non-linear advection terms modify the scaling behavior of the continuous symmetry breaking and stabilize the long-range order, even in $d=2$ far from equilibrium, by means of simple scaling arguments. For an example of the liner advection, we consider the $O(n)$ model in the steady shear. Our scaling analysis reveals that the model can undergo the continuous symmetry breaking even in $d=2$ and, moreover, predicts the upper critical dimension $d_{\rm up}=2$. These results are fully consistent with a recent numerical simulation of the $O(2)$ model, where the mean-field critical exponents are observed even in $d=2$. For an example of the non-linear advection, we consider the Toner-Tu hydrodynamic theory, which was introduced to explain polar-ordered flocks, such as the Vicsek model. Our simple scaling argument reproduces the previous results by the dynamical renormalization theory. Furthermore, we discuss the effects of the additional non-linear terms discovered by the recent re-analysis of the hydrodynamic equation. Our scaling argument predicts that the additional non-linear terms modify the scaling exponents and, in particular, recover the isotropic scaling reported in a previous numerical simulation of the Vicsek model. We discuss that the critical exponents predicted by the naive scaling theory become exact in $d=2$ by using a symmetry consideration and similar argument proposed by Toner and Tu.

In a recent paper [1], Sasa, Hiura, Nakagawa, and Yoshida showed that a natural extension of the minimum work principle to small systems uniquely determines the factor $N!$ that arrises in relations connecting statistical mechanical functions (such as the partition function) and thermodynamic functions (such as the free energy). We believe that this provides us with the clearest answer to the "puzzle" in classical statistical mechanics that goes back to Gibbs. Here we attempt at explaining the theory of Sasa, Hiura, Nakagawa, and Yoshida [1] by using a process discussed by Horowitz and Parrondo [2] in a different context. Although the content of the present note should be obvious to anybody familiar with both [1] and [2], we believe it is useful to have a commentary that presents the same theory from a slightly different perspective. The present note is written in a self-contained manner. We only assume basic knowledge of classical statistical mechanics and thermodynamics. We nevertheless invite the reader to refer to the original paper [2] for background, references, and related discussions, as well as the original thoughts.

We investigate the tightness and optimality of thermodynamic-uncertainty-relation (TUR)-type inequalities from two aspects, the choice of the Fisher information and the class of possible observables. We show that there exists the best choice of the Fisher information, given by the pseudo entropy production, and all other TUR-type inequalities in a certain class can be reproduced by this tightest inequality. We also demonstrate that if we observe not only generalized currents but generalized empirical measures, the TUR-type inequality becomes optimal in the sense that it achieves its equality in general nonequilibrium stationary systems. Combining these results, we can draw a hierarchical structure of TUR-type inequalities.

We derive quantum analogues of Jarzynski's relations, and discuss two applications, namely, a derivation of the law of entropy increase for general compound systems, and a preliminary analysis of heat transfer between two quantum systems at different temperatures. We believe that the derivation of the law of entropy increase is new and of importance.

Higher rank gauge theories are generalizations of electromagnetism where, in addition to overall charge conservation, there is also conservation of higher rank multipoles such as the total dipole moment. In this work we study a four dimensional lattice tensor gauge theory coupled to bosonic matter which has second rank tensor electric and magnetic fields and charge conservation on individual planes. Starting from the Hamiltonian, we derive the lattice action for the gauge fields coupled to $q=1,2$ charged scalars. We use the action formulation to carry out Monte Carlo simulations to map the phase diagram as a function of the gauge ($\beta$) and matter ($\kappa$) couplings. We compute the nature of correlators at strong and weak coupling in the pure gauge theory and compare the results to numerical simulations. Simulations show that the naive weak coupling regime (small $\kappa$, large $\beta$) does not survive in the thermodynamic limit. Instead, the strong coupling confined phase, spans the whole phase diagram. It is a proliferation of instantons that destroys the weak coupling phase and we show, via a duality transformation, that the expected strong confinement is present in the analog of Wilson line correlators. For finite matter coupling at $q=1$ we find a single thermodynamic phase albeit with a first order phase transition terminating in a critical this http URL $q=2$ it is known that the the X-cube model with $\mathbb{Z}_2$ fractonic topological order is recovered deep in the Higgs regime. The simulations indeed reveal a distinct Higgs phase in this case.