Recent progress in observing and manipulating mechanical oscillators at quantum regime provides new opportunities of studying fundamental physics, for example, to search for low energy signatures of quantum gravity. For example, it was recently proposed that such devices can be used to test quantum gravity effects, by detecting the change in the [x,p] commutation relation that could result from quantum gravity corrections. We show that such a correction results in a dependence of a resonant frequency of a mechanical oscillator on its amplitude, which is known as amplitude-frequency effect. By implementing this new method we measure amplitude-frequency effect for 0.3 kg ultra high-Q sapphire split-bar mechanical resonator and for 10 mg quartz bulk acoustic wave resonator. Our experiments with sapphire resonator have established the upper limit on quantum gravity correction constant for \beta_0<5 \times10^6 which is a factor of 6 better than previously detected. The reasonable estimates of $\beta_0$ from experiments with quartz resonators yield an even more stringent limit of $4\times10^4$. The data sets of 1936 measurement of physical pendulum period by Atkinson results in significantly stronger limitations on $\beta_0 \ll 1$. Yet, due to the lack of proper pendulum frequency stability measurement in these experiments, the exact upper bound on $\beta_0$ can not be reliably established. Moreover, pendulum based systems only allow testing a specific form of the modified commutator that depends on the mean value of momentum. The electro-mechanical oscillators to the contrary enable testing of any form of generalized uncertainty principle directly due to much higher stability and a higher degree of control.

We analyze the phase-noise measurement methods in which correlation and averaging is used to reject the background noise of the instrument. All the known methods make use of a mixer, used either as a saturated phase detector or as a linear synchronous detector. Unfortunately, AM noise is taken in through the power-to-dc-offset conversion mechanism that results from the mixer asymmetry. The measurement of some mixers indicates that the unwanted amplitude-to-voltage gain is of the order of 5-50 mV, which is 12-35 dB lower than the phase-to-voltage gain of the mixer. In addition, the trick of setting the mixer at a sweet point -- off the quadrature condition -- where the sensitivity to AM nulls, works only with microwave mixers. The HF-VHF mixers have not this sweet point. Moreover, we prove that if the AM noise comes from the oscillator under test, it can not be rejected by correlation. At least not with the schemes currently used. An example shows that at some critical frequencies the unwanted effect of AM noise is of the same order -- if not greater -- than the phase noise. Thus, experimental mistakes are around the corner.

This paper introduces the multi-freq-ldpy Python package for multiple frequency estimation under Local Differential Privacy (LDP) guarantees. LDP is a gold standard for achieving local privacy with several real-world implementations by big tech companies such as Google, Apple, and Microsoft. The primary application of LDP is frequency (or histogram) estimation, in which the aggregator estimates the number of times each value has been reported. The presented package provides an easy-to-use and fast implementation of state-of-the-art solutions and LDP protocols for frequency estimation of: single attribute (i.e., the building blocks), multiple attributes (i.e., multidimensional data), multiple collections (i.e., longitudinal data), and both multiple attributes/collections. Multi-freq-ldpy is built on the well-established Numpy package -- a de facto standard for scientific computing in Python -- and the Numba package for fast execution. These features are described and illustrated in this paper with four worked examples. This package is open-source and publicly available under an MIT license via GitHub (this https URL) and can be installed via PyPI (this https URL).

The model of a non-autonomous memristor-based oscillator with a line of equilibria is studied. A numerical simulation of the system driven by a periodical force is combined with a theoretical analysis by means of the quasi-harmonic reduction. Both two mechanisms of synchronization are demonstrated: capture of the phase and frequency of oscillations and suppression by an external signal. Classification of undamped oscillations in an autonomous system with a line of equilibria as a special kind of self-sustained oscillations is concluded due to the possibility to observe the effect of frequency-phase locking in the same system in the presence of an external influence. It is established that the occurrence of phase locking in the considered system continuously depends both on parameter values and initial conditions. The simultaneous dependence of synchronization area boundaries on the initial conditions and the parameter values is also shown.

We present a stability analysis of the Lugiato-Lefever model for Kerr optical frequency combs in whispering gallery mode resonators pumped in the anomalous dispersion regime. This article is the second part of a research work whose first part was devoted to the regime of normal dispersion, and was presented in ref. \cite{Part_I}. The case of anomalous dispersion is indeed the most interesting from the theoretical point of view, because of the considerable variety of dynamical behaviors that can be observed. From a technological point of view, it is also the most relevant because it corresponds to the regime where Kerr combs are predominantly generated, studied, and used for different applications. In this article, we analyze the connection between the spatial patterns and the bifurcation structure of the eigenvalues associated to the various equilibria of the system. The bifurcation map evidences a considerable richness from a dynamical standpoint. We study in detail the emergence of super- and sub-critical Turing patterns in the system. We determine the areas were bright isolated cavity solitons emerge, and we show that soliton molecules can emerge as well. Very complex temporal patterns can actually be observed in the system, where solitons (or soliton complexes) co-exist with or without mutual interactions. Our investigations also unveil the mechanism leading to the phenomenon of breathing solitons. Two routes to chaos in the system are identified, namely a route via the so called secondary combs, and another via soliton breathers. The Kerr combs corresponding to all these temporal patterns are analyzed in detail, and a discussion is led about the possibility to gain synthetic comprehension of the observed spectra out of the dynamical complexity of the system.

Compute the coarsest simulation preorder included in an initial preorder is used to reduce the resources needed to analyze a given transition system. This technique is applied on many models like Kripke structures, labeled graphs, labeled transition systems or even word and tree automata. Let (Q, $\rightarrow$) be a given transition system and Rinit be an initial preorder over Q. Until now, algorithms to compute Rsim , the coarsest simulation included in Rinit , are either memory efficient or time efficient but not both. In this paper we propose the foundation for a series of efficient simulation algorithms with the introduction of the notion of maximal transitions and the notion of stability of a preorder with respect to a coarser one. As an illustration we solve an open problem by providing the first algorithm with the best published time complexity, O(|Psim |.|$\rightarrow$|), and a bit space complexity in O(|Psim |^2. log(|Psim |) + |Q|. log(|Q|)), with Psim the partition induced by Rsim.

We investigate the electromechanical properties of quartz bulk acoustic wave resonators at extreme cryogenic temperatures. By applying a DC bias voltage, we demonstrate broad frequency tuning of high-Q phonon modes in a quartz bulk acoustic wave cavity at cryogenic temperatures of 4 K and 20 mK. More than 100 line-widths of tuning of the resonance peak without any degradation in loaded quality factor, which are as high as $1.73\times 10^9$, is seen for high order overtone modes. For all modes and temperatures the observed coefficient of frequency tuning is $\approx$ 3.5 mHz/V per overtone number $n$ corresponding to a maximum of 255.5 mHz/V for the $n = 73$ overtone mode. No degradation in the quality factor is observed for any value of applied biasing field.

Photonic integration of thick holograms in waveguiding structures could be considered the chimera of photonics; multi-faceted and hard to tame. It is the fundamental, and hence indispensable, concept behind compact and monolithically integrated linear optical transformation1. The true relevance of this becomes apparent in the high-dimensional context of unconventional optical computing, that is, in optical neural networks. Yet, integrating such holographic connections is very challenging. It demands high fabrication accuracy, and numerical design of the circuit is often non-tractable for large architectures. Both challenges are intrinsically linked to the usually large refractive index differences between sections of such holographic optical waveguides when using standard techniques of silicon photonics.

The frequency flicker of an oscillator, which appears as a 1/f^3 line in the phase noise spectral density, and as a floor on the Allan variance plot, originates from two basic phenomena, namely: (1) the 1/f phase noise turned into 1/f frequency noise via the Leeson effect, and (2) the 1/f fluctuation of the resonator natural frequency. The discussion on which is the dominant effect, thus on how to improve the stability of the oscillator, has been going on for years without giving a clear answer. This article tackles the question by analyzing the phase noise spectrum of several commercial oscillators and laboratory prototypes, and demonstrates that the fluctuation of the resonator natural frequency is the dominant effect. The investigation method starts from reverse engineering the oscillator phase noise in order to show that if the Leeson effect was dominant, the resonator merit factor Q would be too low as compared to the available technology.

While the use of social robots for language teaching has been explored, there remains limited work on a task-specific synthesized voices for language teaching robots. Given that language is a verbal task, this gap may have severe consequences for the effectiveness of robots for language teaching tasks. We address this lack of L2 teaching robot voices through three contributions: 1. We address the need for a lightweight and expressive robot voice. Using a fine-tuned version of Matcha-TTS, we use emoji prompting to create an expressive voice that shows a range of expressivity over time. The voice can run in real time with limited compute resources. Through case studies, we found this voice more expressive, socially appropriate, and suitable for long periods of expressive speech, such as storytelling. 2. We explore how to adapt a robot's voice to physical and social ambient environments to deploy our voices in various locations. We found that increasing pitch and pitch rate in noisy and high-energy environments makes the robot's voice appear more appropriate and makes it seem more aware of its current environment. 3. We create an English TTS system with improved clarity for L2 listeners using known linguistic properties of vowels that are difficult for these listeners. We used a data-driven, perception-based approach to understand how L2 speakers use duration cues to interpret challenging words with minimal tense (long) and lax (short) vowels in English. We found that the duration of vowels strongly influences the perception for L2 listeners and created an "L2 clarity mode" for Matcha-TTS that applies a lengthening to tense vowels while leaving lax vowels unchanged. Our clarity mode was found to be more respectful, intelligible, and encouraging than base Matcha-TTS while reducing transcription errors in these challenging tense/lax minimal pairs.

For the past few years, in the race between image steganography and steganalysis, deep learning has emerged as a very promising alternative to steganalyzer approaches based on rich image models combined with ensemble classifiers. A key knowledge of image steganalyzer, which combines relevant image features and innovative classification procedures, can be deduced by a deep learning approach called Convolutional Neural Networks (CNN). These kind of deep learning networks is so well-suited for classification tasks based on the detection of variations in 2D shapes that it is the state-of-the-art in many image recognition problems. In this article, we design a CNN-based steganalyzer for images obtained by applying steganography with a unique embedding key. This one is quite different from the previous study of {\em Qian et al.} and its successor, namely {\em Pibre et al.} The proposed architecture embeds less convolutions, with much larger filters in the final convolutional layer, and is more general: it is able to deal with larger images and lower payloads. For the "same embedding key" scenario, our proposal outperforms all other steganalyzers, in particular the existing CNN-based ones, and defeats many state-of-the-art image steganography schemes.

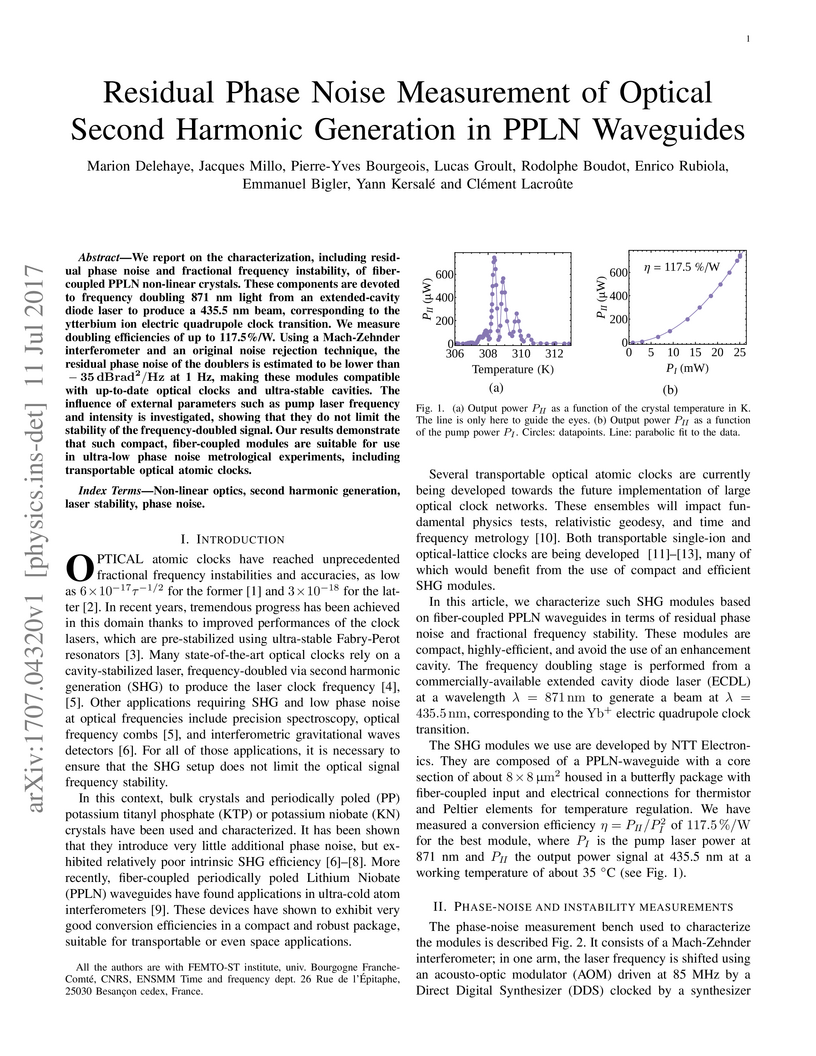
We report on the characterization, including residual phase noise and fractional frequency instability, of fiber-coupled PPLN non-linear crystals. These components are devoted to frequency doubling 871 nm light from an extended-cavity diode laser to produce a 435.5 nm beam, corresponding to the ytterbium ion electric quadrupole clock transition. We measure doubling efficiencies of up to 117.5 %/W. Using a Mach-Zehnder interferometer and an original noise rejection technique, the residual phase noise of the doublers is estimated to be lower than ${\rm -35\, dBrad^2/Hz}$ at 1 Hz, making these modules compatible with up-to-date optical clocks and ultra-stable cavities. The influence of external parameters such as pump laser frequency and intensity is investigated, showing that they do not limit the stability of the frequency-doubled signal. Our results demonstrate that such compact, fiber-coupled modules are suitable for use in ultra-low phase noise metrological experiments, including transportable optical atomic clocks.

The private collection of multiple statistics from a population is a fundamental statistical problem. One possible approach to realize this is to rely on the local model of differential privacy (LDP). Numerous LDP protocols have been developed for the task of frequency estimation of single and multiple attributes. These studies mainly focused on improving the utility of the algorithms to ensure the server performs the estimations accurately. In this paper, we investigate privacy threats (re-identification and attribute inference attacks) against LDP protocols for multidimensional data following two state-of-the-art solutions for frequency estimation of multiple attributes. To broaden the scope of our study, we have also experimentally assessed five widely used LDP protocols, namely, generalized randomized response, optimal local hashing, subset selection, RAPPOR and optimal unary encoding. Finally, we also proposed a countermeasure that improves both utility and robustness against the identified threats. Our contributions can help practitioners aiming to collect users' statistics privately to decide which LDP mechanism best fits their needs.

Polarization plays crucial role in light-matter interactions; hence its overall manipulation is an essential key to unlock the versatility of light manufacturing, especially in femtosecond laser direct writing. Existing polarization-shaping techniques, however, only focus on the manipulation in transverse plane of a light beam, namely a two-dimensional control. In this paper, we propose a novel passive strategy that exploits a class of femtosecond laser written space varying birefringent elements, to shape the polarization state along the optical path. As a demonstration, we generate a three-dimensional structured Bessel beam whose linear polarization state is slowly evolving along the focus (typ. 90 degrees within 60 lightwave periods). Such a "helical polarized" Bessel beam allows imprinting "twisted nanogratings" in SiO2 resulting in an extrinsic optical chirality at a micrometric scale, which owns a high optical rotation. Our work brings new perspectives for three-dimensional polarization manipulations and would find applications in structured light, light-matter interaction and chiral device fabrication.

Given a gene expression data array of a list of bladder cancer patients with their tumor states, it may be difficult to determine which genes can operate as disease markers when the array is large and possibly contains outliers and missing data. An additional difficulty is that observations (tumor states) in the regression problem are discrete ones. In this article, we solve these problems on concrete data using first a clustering approach, followed by Least Absolute Shrinkage and Selection Operator (LASSO) estimators in a nonlinear regression problem involving discrete variables, as described in the brand-new research work of Plan and Vershynin. Gene markers of the most severe tumor state are finally provided using the proposed approach.

Recent extensive numerical experiments in high scale machine learning have allowed to uncover a quite counterintuitive phase transition, as a function of the ratio between the sample size and the number of parameters in the model. As the number of parameters $p$ approaches the sample size $n$, the generalisation error increases, but surprisingly, it starts decreasing again past the threshold $p=n$. This phenomenon, brought to the theoretical community attention in \cite{belkin2019reconciling}, has been thoroughly investigated lately, more specifically for simpler models than deep neural networks, such as the linear model when the parameter is taken to be the minimum norm solution to the least-squares problem, firstly in the asymptotic regime when $p$ and $n$ tend to infinity, see e.g. \cite{hastie2019surprises}, and recently in the finite dimensional regime and more specifically for linear models \cite{bartlett2020benign}, \cite{tsigler2020benign}, \cite{lecue2022geometrical}. In the present paper, we propose a finite sample analysis of non-linear models of \textit{ridge} type, where we investigate the \textit{overparametrised regime} of the double descent phenomenon for both the \textit{estimation problem} and the \textit{prediction} problem. Our results provide a precise analysis of the distance of the best estimator from the true parameter as well as a generalisation bound which complements recent works of \cite{bartlett2020benign} and \cite{chinot2020benign}. Our analysis is based on tools closely related to the continuous Newton method \cite{neuberger2007continuous} and a refined quantitative analysis of the performance in prediction of the minimum $\ell_2$-norm solution.

Optical whispering gallery mode (WGM) resonators have been very attracting platforms for versatile Kerr frequency comb generations. We report a systematic study on the material dispersion of various optical materials that are capable of supporting quality factors above $10^9$. Using an analytical approximation of WGM resonant frequencies in disk resonators, we investigate the effect of the geometry and transverse mode order on the total group-velocity dispersion ($GVD$). We demonstrate that the major radii and the radial mode indices play an important role in tailoring the $GVD$ of WGM resonators. In particular, our study shows that in WGM disk-resonators, the polar families of modes have very similar $GVD$, while the radial families of modes feature dispersion values that can differ by up to several orders of magnitude. The effect of these giant dispersion shifts are experimentally evidenced in Kerr comb generation with magnesium fluoride. From a more general perspective, this critical feature enables to push the zero-dispersion wavelength of fluorite crystals towards the mid-infrared (mid-IR) range, thereby allowing for efficient Kerr comb generation in that spectral range. We show that barium fluoride is the most interesting crystal in this regard, due to its zero dispersion wavelength ($ZDW$) at $1.93 \rm{\mu m}$ and an optimal dispersion profile in the mid-IR regime. We expect our results to facilitate the design of different platforms for Kerr frequency comb generations in both telecommunication and mid-IR spectral ranges.

In this article, we use quantum Langevin equations to provide a theoretical understanding of the non-classical behavior of Kerr optical frequency combs when pumped below and above threshold. In the configuration where the system is under threshold, the pump field is the unique oscillating mode inside the resonator, and triggers the phenomenon of spontaneous four-wave mixing, where two photons from the pump are symmetrically up- and down-converted in the Fourier domain. This phenomenon can only be understood and analyzed from a fully quantum perspective as a consequence of the coupling between the field of the central (pumped) mode and the vacuum fluctuations of the various sidemodes. We analytically calculate the power spectra of the spontaneous emission noise, and we show that these spectra can be either single- or double peaked depending on the parameters of the system. We also calculate as well the overall spontaneous noise power per sidemode, and propose simplified analytical expressions for some particular cases. In the configuration where the system is pumped above threshold, we investigate the phenomena of quantum correlations and multimode squeezed states of light that can occur in the Kerr frequency combs originating from stimulated four-wave mixing. We show that for all stationary spatio-temporal patterns, the side-modes that are symmetrical relatively to the pumped mode in the frequency domain display quantum correlations that can lead to squeezed states of light. We also explicitly determine the phase quadratures leading to photon entanglement, and analytically calculate their quantum noise spectra. We finally discuss the relevance of Kerr combs for quantum information systems at optical telecommunication wavelengths, below and above threshold.

Phase noise and frequency (in)stability both describe the fluctuation of stable periodic signals, from somewhat different standpoints. Frequency is unique compared to other domains of metrology, in that its fluctuations of interest span at least 14 orders of magnitude, from $10^{-4}$ in a mechanical watch to $10^{-18}$ in atomic clocks. The frequency span of interest is some 12-15 orders of magnitude, from $\mu$Hz to GHz Fourier frequency for phase noise, while the time span over which the fluctuations occur ranges from sub-$\mu$s to years integration time for variances. Because this domain is ubiquitous in science and technology, a common language and tools suitable to the variety mentioned are a challenge. This article is at once (1) a tutorial, (2) a review covering the most important facts about phase noise, frequency noise and two-sample (Allan and Allan-like) variances, and (3) a user guide to "Enrico's Chart of Phase Noise and Two-Sample Variances." In turn, the Chart is a reference card collecting the most useful concepts, formulas and plots in a single A4/A-size sheet, intended to be a staple on the desk of whoever works with these topics. The Chart is available under Creative Commons 4.0 CC-BY-NC-ND license from Zenodo, DOI 10.5281/zenodo.4399218. A wealth of auxiliary material is available for free on the Enrico's home page this http URL

We report on the development of an ultrafast beam shaper capable of generating Bessel beams of high cone angle that maintain a high-intensity hot spot with subwavelength diameter over a propagation distance in excess of 8~mm. This generates a high-intensity focal region with extremely high aspect ratio exceeding 10~000:1. The absence of intermediate focusing in the shaper allows for shaping very high energies, up to Joule levels. We demonstrate proof of principle application of the Bessel beam shaper for stealth dicing of thick glass, up to 1~cm. We expect this high energy Bessel beam shaper will have applications in several areas of high intensity laser physics.