By classifying infinite-width neural networks and identifying the *optimal* limit, Tensor Programs IV and V demonstrated a universal way, called $\mu$P, for *widthwise hyperparameter transfer*, i.e., predicting optimal hyperparameters of wide neural networks from narrow ones. Here we investigate the analogous classification for *depthwise parametrizations* of deep residual networks (resnets). We classify depthwise parametrizations of block multiplier and learning rate by their infinite-width-then-depth limits. In resnets where each block has only one layer, we identify a unique optimal parametrization, called Depth-$\mu$P that extends $\mu$P and show empirically it admits depthwise hyperparameter transfer. We identify *feature diversity* as a crucial factor in deep networks, and Depth-$\mu$P can be characterized as maximizing both feature learning and feature diversity. Exploiting this, we find that absolute value, among all homogeneous nonlinearities, maximizes feature diversity and indeed empirically leads to significantly better performance. However, if each block is deeper (such as modern transformers), then we find fundamental limitations in all possible infinite-depth limits of such parametrizations, which we illustrate both theoretically and empirically on simple networks as well as Megatron transformer trained on Common Crawl.

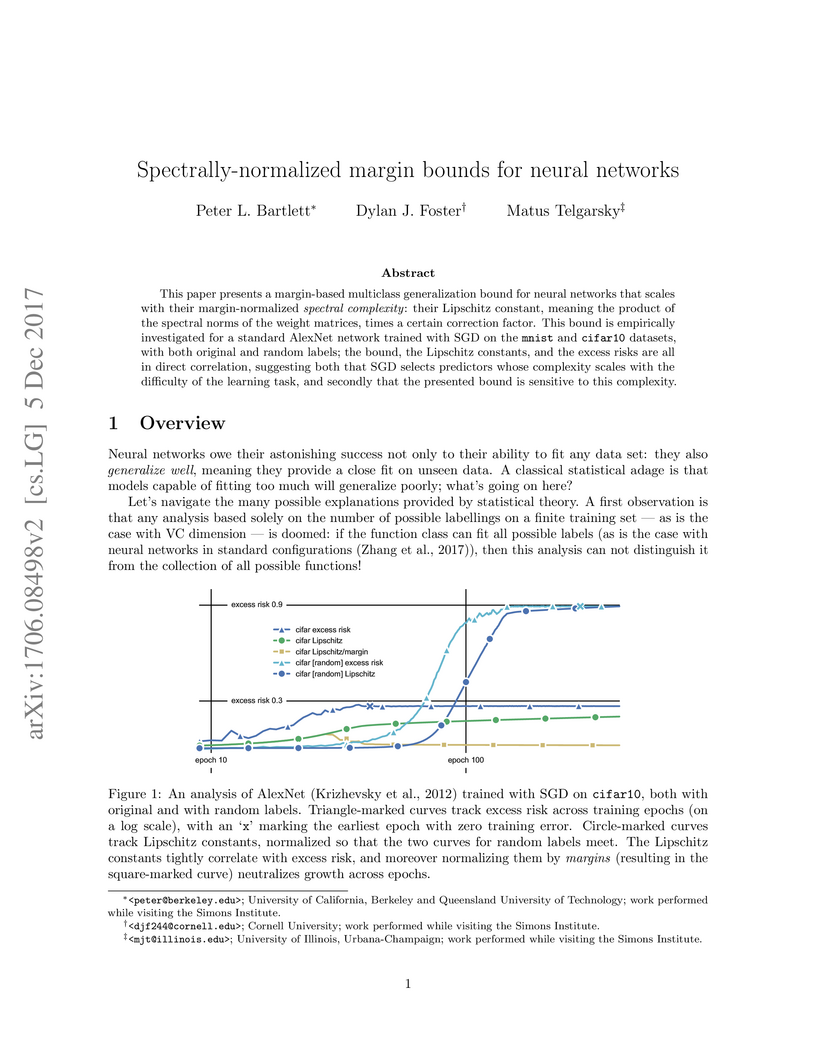
This paper presents a margin-based multiclass generalization bound for neural networks that scales with their margin-normalized "spectral complexity": their Lipschitz constant, meaning the product of the spectral norms of the weight matrices, times a certain correction factor. This bound is empirically investigated for a standard AlexNet network trained with SGD on the mnist and cifar10 datasets, with both original and random labels; the bound, the Lipschitz constants, and the excess risks are all in direct correlation, suggesting both that SGD selects predictors whose complexity scales with the difficulty of the learning task, and secondly that the presented bound is sensitive to this complexity.

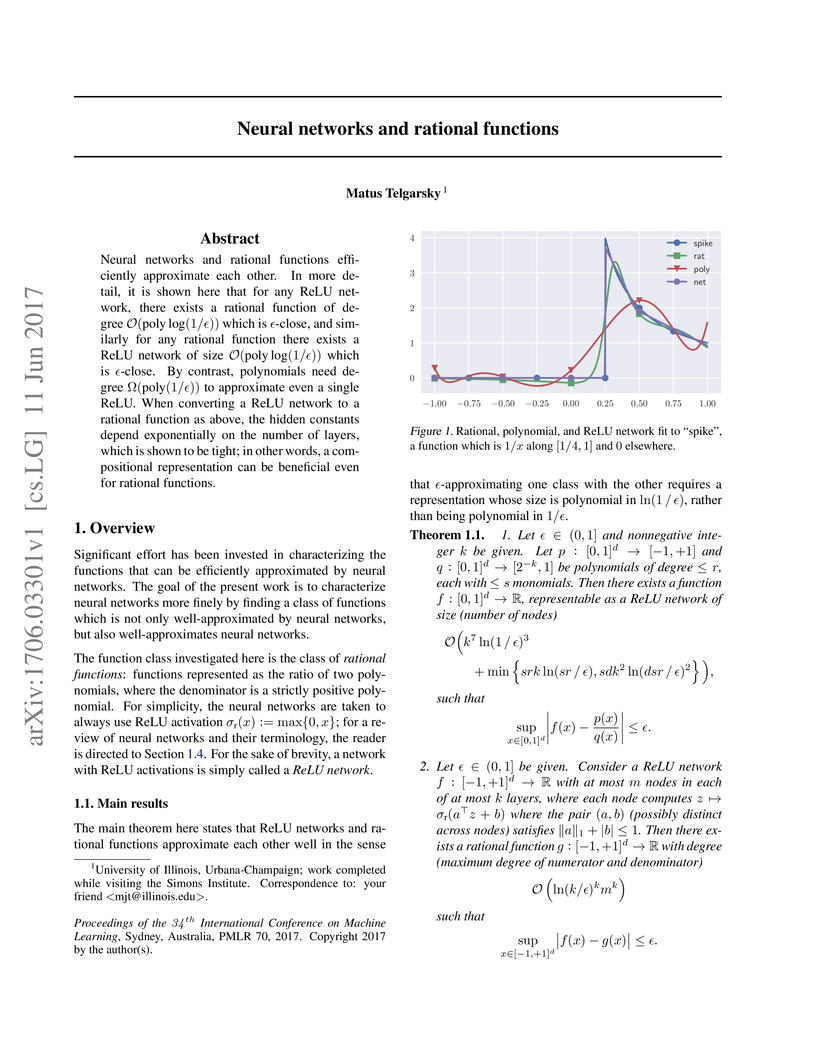
Neural networks and rational functions efficiently approximate each other. In more detail, it is shown here that for any ReLU network, there exists a rational function of degree $O(\text{polylog}(1/\epsilon))$ which is $\epsilon$-close, and similarly for any rational function there exists a ReLU network of size $O(\text{polylog}(1/\epsilon))$ which is $\epsilon$-close. By contrast, polynomials need degree $\Omega(\text{poly}(1/\epsilon))$ to approximate even a single ReLU. When converting a ReLU network to a rational function as above, the hidden constants depend exponentially on the number of layers, which is shown to be tight; in other words, a compositional representation can be beneficial even for rational functions.

We study the error correcting properties of Haar random codes, in which a $K$-dimensional code space $\boldsymbol{C} \subseteq \mathbb{C}^N$ is chosen at random from the Haar distribution. Our main result is that Haar random codes can approximately correct errors up to the quantum Hamming bound, meaning that a set of $m$ Pauli errors can be approximately corrected so long as $mK \ll N$. This is the strongest bound known for any family of quantum error correcting codes (QECs), and continues a line of work showing that approximate QECs can significantly outperform exact QECs [LNCY97, CGS05, BGG24]. Our proof relies on a recent matrix concentration result of Bandeira, Boedihardjo, and van Handel.

Transformers are a class of autoregressive deep learning architectures which have recently achieved state-of-the-art performance in various vision, language, and robotics tasks. We revisit the problem of Kalman Filtering in linear dynamical systems and show that Transformers can approximate the Kalman Filter in a strong sense. Specifically, for any observable LTI system we construct an explicit causally-masked Transformer which implements the Kalman Filter, up to a small additive error which is bounded uniformly in time; we call our construction the Transformer Filter. Our construction is based on a two-step reduction. We first show that a softmax self-attention block can exactly represent a Nadaraya-Watson kernel smoothing estimator with a Gaussian kernel. We then show that this estimator closely approximates the Kalman Filter. We also investigate how the Transformer Filter can be used for measurement-feedback control and prove that the resulting nonlinear controllers closely approximate the performance of standard optimal control policies such as the LQG controller.

The Unitary Synthesis Problem (Aaronson-Kuperberg 2007) asks whether any $n$-qubit unitary $U$ can be implemented by an efficient quantum algorithm $A$ augmented with an oracle that computes an arbitrary Boolean function $f$. In other words, can the task of implementing any unitary be efficiently reduced to the task of implementing any Boolean function? In this work, we prove a one-query lower bound for unitary synthesis. We show that there exist unitaries $U$ such that no quantum polynomial-time oracle algorithm $A^f$ can implement $U$, even approximately, if it only makes one (quantum) query to $f$. Our approach also has implications for quantum cryptography: we prove (relative to a random oracle) the existence of quantum cryptographic primitives that remain secure against all one-query adversaries $A^{f}$. Since such one-query algorithms can decide any language, solve any classical search problem, and even prepare any quantum state, our result suggests that implementing random unitaries and breaking quantum cryptography may be harder than all of these tasks. To prove this result, we formulate unitary synthesis as an efficient challenger-adversary game, which enables proving lower bounds by analyzing the maximum success probability of an adversary $A^f$. Our main technical insight is to identify a natural spectral relaxation of the one-query optimization problem, which we bound using tools from random matrix theory. We view our framework as a potential avenue to rule out polynomial-query unitary synthesis, and we state conjectures in this direction.

The existence of pseudorandom unitaries (PRUs) -- efficient quantum circuits that are computationally indistinguishable from Haar-random unitaries -- has been a central open question, with significant implications for cryptography, complexity theory, and fundamental physics. In this work, we close this question by proving that PRUs exist, assuming that any quantum-secure one-way function exists. We establish this result for both (1) the standard notion of PRUs, which are secure against any efficient adversary that makes queries to the unitary $U$, and (2) a stronger notion of PRUs, which are secure even against adversaries that can query both the unitary $U$ and its inverse $U^\dagger$. In the process, we prove that any algorithm that makes queries to a Haar-random unitary can be efficiently simulated on a quantum computer, up to inverse-exponential trace distance.

The complexity of matrix multiplication is a central topic in computer science. While the focus has traditionally been on exact algorithms, a long line of literature also considers randomized algorithms, which return an approximate solution in faster time. In this work, we adopt a unifying perspective that frames these randomized algorithms in terms of mean estimation. Using it, we first give refined analyses of classical algorithms based on random walks by Cohen-Lewis (`99), and based on sketching by Sarlós (`06) and Drineas-Kannan-Mahoney (`06). We then propose an improvement on Cohen-Lewis that yields a single classical algorithm that is faster than all the other approaches, if we assume no use of (exact) fast matrix multiplication as a subroutine. Second, we demonstrate a quantum speedup on top of these algorithms by using the recent quantum multivariate mean estimation algorithm by Cornelissen-Hamoudi-Jerbi (`22).

We study the linear convergence of variants of the Frank-Wolfe algorithms for some classes of strongly convex problems, using only affine-invariant quantities. As in Guelat & Marcotte (1986), we show the linear convergence of the standard Frank-Wolfe algorithm when the solution is in the interior of the domain, but with affine invariant constants. We also show the linear convergence of the away-steps variant of the Frank-Wolfe algorithm, but with constants which only depend on the geometry of the domain, and not any property of the location of the optimal solution. Running these algorithms does not require knowing any problem specific parameters.

We make several advances broadly related to the maintenance of electrical flows in weighted graphs undergoing dynamic resistance updates, including: 1. More efficient dynamic spectral vertex sparsification, achieved by faster length estimation of random walks in weighted graphs using Morris counters [Morris 1978, Nelson-Yu 2020]. 2. A direct reduction from detecting edges with large energy in dynamic electric flows to dynamic spectral vertex sparsifiers. 3. A procedure for turning algorithms for estimating a sequence of vectors under updates from an oblivious adversary to one that tolerates adaptive adversaries via the Gaussian-mechanism from differential privacy. Combining these pieces with modifications to prior robust interior point frameworks gives an algorithm that on graphs with $m$ edges computes a mincost flow with edge costs and capacities in $[1, U]$ in time $\widetilde{O}(m^{3/2-1/58} \log^2 U)$. In prior and independent work, [Axiotis-Mądry-Vladu FOCS 2021] also obtained an improved algorithm for sparse mincost flows on capacitated graphs. Our algorithm implies a $\widetilde{O}(m^{3/2-1/58} \log U)$ time maxflow algorithm, improving over the $\widetilde{O}(m^{3/2-1/328}\log U)$ time maxflow algorithm of [Gao-Liu-Peng FOCS 2021].

The Aaronson-Ambainis conjecture (Theory of Computing '14) says that every low-degree bounded polynomial on the Boolean hypercube has an influential variable. This conjecture, if true, would imply that the acceptance probability of every $d$-query quantum algorithm can be well-approximated almost everywhere (i.e., on almost all inputs) by a $\mathrm{poly}(d)$-query classical algorithm. We prove a special case of the conjecture: in every completely bounded degree-$d$ block-multilinear form with constant variance, there always exists a variable with influence at least $1/\mathrm{poly}(d)$. In a certain sense, such polynomials characterize the acceptance probability of quantum query algorithms, as shown by Arunachalam, Briët and Palazuelos (SICOMP '19). As a corollary we obtain efficient classical almost-everywhere simulation for a particular class of quantum algorithms that includes for instance $k$-fold Forrelation. Our main technical result relies on connections to free probability theory.

Low-rank approximation and column subset selection are two fundamental and related problems that are applied across a wealth of machine learning applications. In this paper, we study the question of socially fair low-rank approximation and socially fair column subset selection, where the goal is to minimize the loss over all sub-populations of the data. We show that surprisingly, even constant-factor approximation to fair low-rank approximation requires exponential time under certain standard complexity hypotheses. On the positive side, we give an algorithm for fair low-rank approximation that, for a constant number of groups and constant-factor accuracy, runs in $2^{\text{poly}(k)}$ time rather than the naïve $n^{\text{poly}(k)}$, which is a substantial improvement when the dataset has a large number $n$ of observations. We then show that there exist bicriteria approximation algorithms for fair low-rank approximation and fair column subset selection that run in polynomial time.

Stochastic Gradient Langevin Dynamics (SGLD) is a popular variant of Stochastic Gradient Descent, where properly scaled isotropic Gaussian noise is added to an unbiased estimate of the gradient at each iteration. This modest change allows SGLD to escape local minima and suffices to guarantee asymptotic convergence to global minimizers for sufficiently regular non-convex objectives (Gelfand and Mitter, 1991). The present work provides a nonasymptotic analysis in the context of non-convex learning problems, giving finite-time guarantees for SGLD to find approximate minimizers of both empirical and population risks. As in the asymptotic setting, our analysis relates the discrete-time SGLD Markov chain to a continuous-time diffusion process. A new tool that drives the results is the use of weighted transportation cost inequalities to quantify the rate of convergence of SGLD to a stationary distribution in the Euclidean $2$-Wasserstein distance.

Synthetic data has gained attention for training large language models, but poor-quality data can harm performance (see, e.g., Shumailov et al. (2023); Seddik et al. (2024)). A potential solution is data pruning, which retains only high-quality data based on a score function (human or machine feedback). Previous work Feng et al. (2024) analyzed models trained on synthetic data as sample size increases. We extend this by using random matrix theory to derive the performance of a binary classifier trained on a mix of real and pruned synthetic data in a high dimensional setting. Our findings identify conditions where synthetic data could improve performance, focusing on the quality of the generative model and verification strategy. We also show a smooth phase transition in synthetic label noise, contrasting with prior sharp behavior in infinite sample limits. Experiments with toy models and large language models validate our theoretical results.

Given a non-negative $n \times n$ matrix viewed as a set of distances between $n$ points, we consider the property testing problem of deciding if it is a metric. We also consider the same problem for two special classes of metrics, tree metrics and ultrametrics. For general metrics, our paper is the first to consider these questions. We prove an upper bound of $O(n^{2/3}/\epsilon^{4/3})$ on the query complexity for this problem. Our algorithm is simple, but the analysis requires great care in bounding the variance on the number of violating triangles in a sample. When $\epsilon$ is a slowly decreasing function of $n$ (rather than a constant, as is standard), we prove a lower bound of matching dependence on $n$ of $\Omega (n^{2/3})$, ruling out any property testers with $o(n^{2/3})$ query complexity unless their dependence on $1/\epsilon$ is super-polynomial. Next, we turn to tree metrics and ultrametrics. While there were known upper and lower bounds, we considerably improve these bounds showing essentially tight bounds of $\tilde{O}(1/\epsilon )$ on the sample complexity. We also show a lower bound of $\Omega ( 1/\epsilon^{4/3} )$ on the query complexity. Our upper bounds are derived by doing a more careful analysis of a natural, simple algorithm. For the lower bounds, we construct distributions on NO instances, where it is hard to find a witness showing that these are not ultrametrics.