data-structures-and-algorithms
We study the following distribution clustering problem: Given a hidden partition of k distributions into two groups, such that the distributions within each group are the same, and the two distributions associated with the two clusters are ε-far in total variation, the goal is to recover the partition. We establish upper and lower bounds on the sample complexity for two fundamental cases: (1) when one of the cluster's distributions is known, and (2) when both are unknown. Our upper and lower bounds characterize the sample complexity's dependence on the domain size n, number of distributions k, size r of one of the clusters, and distance ε. In particular, we achieve tightness with respect to (n,k,r,ε) (up to an O(logk) factor) for all regimes.
In 2021, Gupta and Suzumura proposed a novel algorithm for enumerating all bounded-length simple cycles in directed graphs. In this work, we present concrete examples demonstrating that the proposed algorithm fails to enumerate certain valid cycles. Via these examples, we perform a detailed analysis pinpointing the specific points at which the proofs exhibit logical gaps. Furthermore, we propose a corrected formulation that resolves these issues while preserving the desirable property that the algorithm's computational complexity remains O((c+1)⋅k⋅(n+e)) where c is the number of simple cycles of a specified maximum length k, and n and e the number of graph nodes and edges respectively.
While modern language models and their inner workings are incredibly complex, recent work (Golowich, Liu & Shetty; 2025) has proposed a simple and potentially tractable abstraction for them through the observation that empirically, these language models all seem to have approximately low logit rank. Roughly, this means that a matrix formed by the model's log probabilities of various tokens conditioned on certain sequences of tokens is well approximated by a low rank matrix.
In this paper, our focus is on understanding how this structure can be exploited algorithmically for obtaining provable learning guarantees. Since low logit rank models can encode hard-to-learn distributions such as noisy parities, we study a query learning model with logit queries that reflects the access model for common APIs. Our main result is an efficient algorithm for learning any approximately low logit rank model from queries. We emphasize that our structural assumption closely reflects the behavior that is empirically observed in modern language models. Thus, our result gives what we believe is the first end-to-end learning guarantee for a generative model that plausibly captures modern language models.
We study the classic problem of prediction with expert advice under the constraint of local differential privacy (LDP). In this context, we first show that a classical algorithm naturally satisfies LDP and then design two new algorithms that improve it: RW-AdaBatch and RW-Meta. For RW-AdaBatch, we exploit the limited-switching behavior induced by LDP to provide a novel form of privacy amplification that grows stronger on easier data, analogous to the shuffle model in offline learning. Drawing on the theory of random walks, we prove that this improvement carries essentially no utility cost. For RW-Meta, we develop a general method for privately selecting between experts that are themselves non-trivial learning algorithms, and we show that in the context of LDP this carries no extra privacy cost. In contrast, prior work has only considered data-independent experts. We also derive formal regret bounds that scale inversely with the degree of independence between experts. Our analysis is supplemented by evaluation on real-world data reported by hospitals during the COVID-19 pandemic; RW-Meta outperforms both the classical baseline and a state-of-the-art \textit{central} DP algorithm by 1.5-3× on the task of predicting which hospital will report the highest density of COVID patients each week.
Fast exact algorithms are known for Hamiltonian paths in undirected and directed bipartite graphs through elegant though involved algorithms that are quite different from each other. We devise algorithms that are simple and similar to each other while having the same upper bounds. The common features of these algorithms is the use of the Matrix-Tree theorem and sieving using roots of unity.
Next, we use the framework to provide alternative algorithms to count perfect matchings in bipartite graphs on n vertices, i.e., computing the {0,1}-permanent of a square n/2×n/2 matrix which runs in a time similar to Ryser.
We demonstrate the flexibility of our method by counting the number of ways to vertex partition the graph into k-stars (a k-star consist of a tree with a root having k−1 children that are all leaves). Interestingly, our running time improves to O∗((1+ϵk)n) with ϵk→0 as k→∞.
As an aside, making use of Björklund's algorithm for exact counting perfect matchings in general graphs, we show that the count of maximum matchings can be computed in time O∗(2ν) where ν is the size of a maximum matching. The crucial ingredient here is the famous Gallai-Edmonds decomposition theorem.
All our algorithms run in polynomial space.
We study the problem of certifying local Hamiltonians from real-time access to their dynamics. Given oracle access to e−itH for an unknown k-local Hamiltonian H and a fully specified target Hamiltonian H0, the goal is to decide whether H is exactly equal to H0 or differs from H0 by at least ε in normalized Frobenius norm, while minimizing the total evolution time. We introduce the first intolerant Hamiltonian certification protocol that achieves optimal performance for all constant-locality Hamiltonians. For general n-qubit, k-local, traceless Hamiltonians, our procedure uses O(ck/ε) total evolution time for a universal constant c, and succeeds with high probability. In particular, for O(1)-local Hamiltonians, the total evolution time becomes Θ(1/ε), matching the known Ω(1/ε) lower bounds and achieving the gold-standard Heisenberg-limit scaling. Prior certification methods either relied on implementing inverse evolution of H, required controlled access to e−itH, or achieved near-optimal guarantees only in restricted settings such as the Ising case (k=2). In contrast, our algorithm requires neither inverse evolution nor controlled operations: it uses only forward real-time dynamics and achieves optimal intolerant certification for all constant-locality Hamiltonians.
We present a data structure that we call a Dynamic Representative Set. In its most basic form, it is given two parameters 0< k < n and allows us to maintain a representation of a family F of subsets of {1,…,n}. It supports basic update operations (unioning of two families, element convolution) and a query operation that determines for a set B⊆{1,…,n} whether there is a set A∈F of size at most k−∣B∣ such that A and B are disjoint. After 2k+O(klog2k)nlogn preprocessing time, all operations use 2k+O(klog2k)logn time.
Our data structure has many algorithmic consequences that improve over previous works. One application is a deterministic algorithm for the Weighted Directed k-Path problem, one of the central problems in parameterized complexity. Our algorithm takes as input an n-vertex directed graph G=(V,E) with edge lengths and an integer k, and it outputs the minimum edge length of a path on k vertices in 2k+O(klog2k)(n+m)logn time (in the word RAM model where weights fit into a single word). Modulo the lower order term 2O(klog2k), this answers a question that has been repeatedly posed as a major open problem in the field.
We consider the fundamental problem of balanced k-means clustering. In particular, we introduce an optimal transport approach to alternating minimization called BalLOT, and we show that it delivers a fast and effective solution to this problem. We establish this with a variety of numerical experiments before proving several theoretical guarantees. First, we prove that for generic data, BalLOT produces integral couplings at each step. Next, we perform a landscape analysis to provide theoretical guarantees for both exact and partial recoveries of planted clusters under the stochastic ball model. Finally, we propose initialization schemes that achieve one-step recovery of planted clusters.
Researchers from Nanjing University and MIT's CSAIL developed a unified FPT-time approximation framework, yielding a (3 + ",")-approximation for minimum-norm capacitated k-clustering and a tight 3-approximation for capacitated k-center. The framework also delivered a tight (min{3, 1 + 2/ec} + "," )-approximation for uncapacitated top-cn norm k-clustering, significantly advancing theoretical guarantees for these problems.
Snarls and superbubbles are fundamental pangenome decompositions capturing variant sites. These bubble-like structures underpin key tasks in computational pangenomics, including structural-variant genotyping, distance indexing, haplotype sampling, and variant annotation. Snarls can be quadratically-many in the size of the graph, and since their introduction in 2018 with the vg toolkit, there has been no work on identifying all snarls in linear time. Moreover, while it is known how to find superbubbles in linear time, this result is a highly specialized solution only achieved after a long series of papers.
We present the first algorithm identifying all snarls in linear time. This is based on a new representation of all snarls, of size linear in the input graph size, and which can be computed in linear time. Our algorithm is based on a unified framework that also provides a new linear-time algorithm for finding superbubbles. An observation behind our results is that all such structures are separated from the rest of the graph by two vertices (except for cases which are trivially computable), i.e. their endpoints are a 2-separator of the underlying undirected graph. Based on this, we employ the well-known SPQR tree decomposition, which encodes all 2-separators, to guide a traversal that finds the bubble-like structures efficiently.
We implemented our algorithms in C++ (available at this https URL) and evaluated them on various pangenomic datasets. Our algorithms outcompete or they are on the same level of existing methods. For snarls, we are up to two times faster than vg, while identifying all snarls. When computing superbubbles, we are up to 50 times faster than BubbleGun. Our SPQR tree framework provides a unifying perspective on bubble-like structures in pangenomics, together with a template for finding other bubble-like structures efficiently.
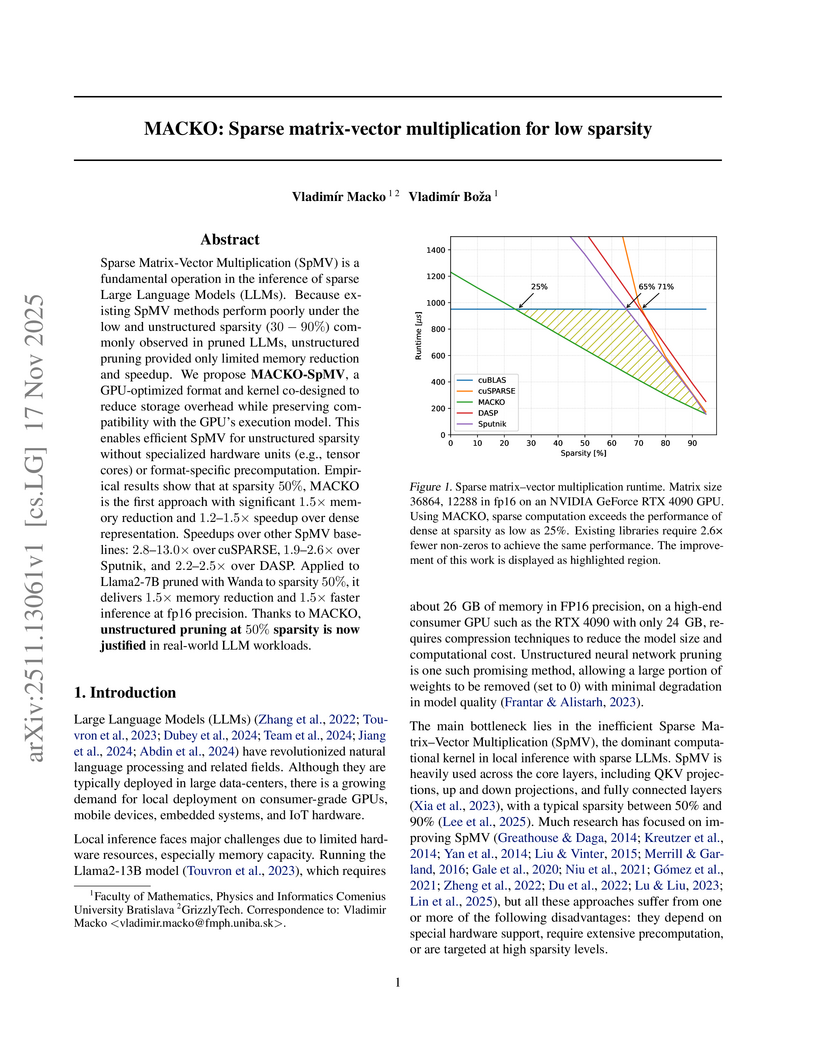
MACKO introduces a novel sparse matrix-vector multiplication (SpMV) method and storage format tailored for low and unstructured sparsity in Large Language Models (LLMs) on GPUs. This approach enables practical deployment of pruned LLMs, achieving up to 1.5x speedup and 1.5x memory reduction for Llama2-7B at 50% sparsity compared to dense computation.
Researchers from Columbia, Harvard, MIT, and Waterloo establish sample complexity bounds for learning and testing high-dimensional, real-valued Lipschitz convex functions under a standard Gaussian measure. Their work introduces algorithms achieving polynomial sample complexity in dimension for agnostic learning and two-sided testing, and derives a correlational statistical query lower bound for agnostic learning.
A graph G is a circle graph if it is an intersection graph of chords of a unit circle. We give an algorithm that takes as input an n vertex circle graph G, runs in time at most nO(logn) and finds a proper 3-coloring of G, if one exists. As a consequence we obtain an algorithm with the same running time to determine whether a given ordered graph (G,≺) has a 3-page book embedding. This gives a partial resolution to the well known open problem of Dujmović and Wood [Discret. Math. Theor. Comput. Sci. 2004], Eppstein [2014], and Bachmann, Rutter and Stumpf [J. Graph Algorithms Appl. 2024] of whether 3-Coloring on circle graphs admits a polynomial time algorithm.
Given a graph and a pair of terminals s, t, the next-to-shortest path problem asks for an s→t (simple) path that is shortest among all not shortest s→t paths (if one exists). This problem was introduced in 1996, and soon after was shown to be NP-complete for directed graphs with non-negative edge weights, leaving open the case of positive edge weights. Subsequent work investigated this open question, and developed polynomial-time algorithms for the cases of undirected graphs and planar directed graphs. In this work, we resolve this nearly 30-year-old open problem by providing an algorithm for the next-to-shortest path problem on directed graphs with positive edge weights.
The torrential influx of floating-point data from domains like IoT and HPC necessitates high-performance lossless compression to mitigate storage costs while preserving absolute data fidelity. Leveraging GPU parallelism for this task presents significant challenges, including bottlenecks in heterogeneous data movement, complexities in executing precision-preserving conversions, and performance degradation due to anomaly-induced sparsity. To address these challenges, this paper introduces a novel GPU-based framework for floating-point adaptive lossless compression. The proposed solution employs three key innovations: a lightweight asynchronous pipeline that effectively hides I/O latency during CPU-GPU data transfer; a fast and theoretically guaranteed float-to-integer conversion method that eliminates errors inherent in floating-point arithmetic; and an adaptive sparse bit-plane encoding strategy that mitigates the sparsity caused by outliers. Extensive experiments on 12 diverse datasets demonstrate that the proposed framework significantly outperforms state-of-the-art competitors, achieving an average compression ratio of 0.299 (a 9.1% relative improvement over the best competitor), an average compression throughput of 10.82 GB/s (2.4x higher), and an average decompression throughput of 12.32 GB/s (2.4x higher).
Analysis of entire programs as a single unit, or whole-program analysis, involves propagation of large amounts of information through the control flow of the program. This is especially true for pointer analysis, where, unless significant compromises are made in the precision of the analysis, there is a combinatorial blowup of information. One of the key problems we observed in our own efforts to this end is that a lot of duplicate data was being propagated, and many low-level data structure operations were repeated a large number of times.
We present what we consider to be a novel and generic data structure, LatticeHashForest (LHF), to store and operate on such data in a manner that eliminates a majority of redundant computations and duplicate data in scenarios similar to those encountered in compilers and program optimization. LHF differs from similar work in this vein, such as hash-consing, ZDDs, and BDDs, by not only providing a way to efficiently operate on large, aggregate structures, but also modifying the elements of such structures in a manner that they can be deduplicated immediately. LHF also provides a way to perform a nested construction of elements such that they can be deduplicated at multiple levels, cutting down the need for additional, nested computations.
We provide a detailed structural description, along with an abstract model of this data structure. An entire C++ implementation of LHF is provided as an artifact along with evaluations of LHF using examples and benchmark programs. We also supply API documentation and a user manual for users to make independent applications of LHF. Our main use case in the realm of pointer analysis shows memory usage reduction to an almost negligible fraction, and speedups beyond 4x for input sizes approaching 10 million when compared to other implementations.
Vizing's theorem states that any n-vertex m-edge graph of maximum degree Δ can be edge colored using at most Δ+1 different colors. Vizing's original proof is easily translated into a deterministic O(mn) time algorithm. This deterministic time bound was subsequently improved to O~(mn) time, independently by [Arjomandi, 1982] and by [Gabow et al., 1985].
A series of recent papers improved the time bound of O~(mn) using randomization, culminating in the randomized near-linear time (Δ+1)-coloring algorithm by [Assadi, Behnezhad, Bhattacharya, Costa, Solomon, and Zhang, 2025]. At the heart of all of these recent improvements, there is some form of a sublinear time algorithm. Unfortunately, sublinear time algorithms as a whole almost always require randomization. This raises a natural question: can the deterministic time complexity of the problem be reduced below the O~(mn) barrier?
In this paper, we answer this question in the affirmative. We present a deterministic almost-linear time (Δ+1)-coloring algorithm, namely, an algorithm running in m⋅2O(logΔ)⋅logn=m1+o(1) time. Our main technical contribution is to entirely forego sublinear time algorithms. We do so by presenting a new deterministic color-type sparsification approach that runs in almost-linear (instead of sublinear) time, but can be used to color a much larger set of edges.
Test-time algorithms that combine the generative power of language models with process verifiers that assess the quality of partial generations offer a promising lever for eliciting new reasoning capabilities, but the algorithmic design space and computational scaling properties of such approaches are still opaque, and their benefits are far from apparent when one accounts for the cost of learning a high-quality verifier. Our starting point is the observation that seemingly benign errors in a learned verifier can lead to catastrophic failures for standard decoding techniques due to error amplification during the course of generation. We then ask: can this be improved with more sophisticated decoding strategies?
We introduce a new process-guided test-time sampling algorithm, VGB, which uses theoretically grounded backtracking to achieve provably better robustness to verifier errors. VGB interprets autoregressive generation as a random walk on a tree of partial generations, with transition probabilities guided by the process verifier and base model; crucially, backtracking occurs probabilistically. This process generalizes the seminal Sinclair-Jerrum random walk (Sinclair & Jerrum, 1989) from the literature on approximate counting and sampling in theoretical computer science, and a conceptual contribution of our work is to highlight parallels with this literature. Empirically, we demonstrate on both synthetic and real language modeling tasks that VGB outperforms baselines on a variety of metrics.
We survey different perspectives on the stochastic localization process of [Eld13], a powerful construction that has had many exciting recent applications in high-dimensional probability and algorithm design. Unlike prior surveys on this topic, our focus is on giving a self-contained presentation of all known alternative constructions of Eldan's stochastic localization, with an emphasis on connections between different constructions. Our hope is that by collecting these perspectives, some of which had primarily arisen within a particular community (e.g., probability theory, theoretical computer science, information theory, or machine learning), we can broaden the accessibility of stochastic localization, and ease its future use.
Random matrix theory has played a major role in several areas of pure and applied mathematics, as well as statistics, physics, and computer science. This lecture aims to describe the intrinsic freeness phenomenon and how it provides new easy-to-use sharp non-asymptotic bounds on the spectrum of general random matrices. We will also present a couple of illustrative applications in high dimensional statistical inference. This article accompanies a lecture that will be given by the author at the International Congress of Mathematicians in Philadelphia in the Summer of 2026.
There are no more papers matching your filters at the moment.