Automated driving has the potential to revolutionize personal, public, and freight mobility. Beside accurately perceiving the environment, automated vehicles must plan a safe, comfortable, and efficient motion trajectory. To promote safety and progress, many works rely on modules that predict the future motion of surrounding traffic. Modular automated driving systems commonly handle prediction and planning as sequential, separate tasks. While this accounts for the influence of surrounding traffic on the ego vehicle, it fails to anticipate the reactions of traffic participants to the ego vehicle's behavior. Recent methods increasingly integrate prediction and planning in a joint or interdependent step to model bidirectional interactions. To date, a comprehensive overview of different integration principles is lacking. We systematically review state-of-the-art deep learning-based planning systems, and focus on how they integrate prediction. Different facets of the integration ranging from system architecture to high-level behavioral aspects are considered and related to each other. Moreover, we discuss the implications, strengths, and limitations of different integration principles. By pointing out research gaps, describing relevant future challenges, and highlighting trends in the research field, we identify promising directions for future research.

We propose a practical benchmarking suite inspired by physical dynamics to challenge both quantum and classical computers. Using a parallel in time encoding, we convert the real-time propagator of an $n$-qubit, possibly non-Hermitian, Hamiltonian into a quadratic-unconstrained binary optimisation (QUBO) problem. The resulting QUBO instances are executed on D-Wave quantum annealers as well as using two classical solvers, Simulated Annealing and VeloxQ, a state-of-the-art classical heuristic solver. This enables a direct comparison. To stress-test the workflow, we use eight representative models, divided into three groups: (i)~single-qubit rotations, (ii)~multi-qubit entangling gates (Bell, GHZ, cluster), and (iii)~$\text{PT}$-symmetric, parity-conserving and other non-Hermitian generators. Across this diverse suite we track the success probability and time to solution, which are well established measures in the realm of heuristic combinatorial optimisation. Our results show that D-Wave Advantage2 consistently surpasses its predecessor, while VeloxQ presently retains the overall lead, reflecting the maturity of classical optimisers. We highlight the rapid progress of analog quantum optimisation, and suggest a clear trajectory toward quantum competitive dynamics simulation, by establishing the parallel in time QUBO framework as a versatile test-bed for tracking and evaluating that progress.

The dynamical low-rank approximation of time-dependent matrices is a low-rank factorization updating technique. It leads to differential equations for factors of the matrices, which need to be solved numerically. We propose and analyze a fully ex- plicit, computationally inexpensive integrator that is based on splitting the orthogonal projector onto the tangent space of the low-rank manifold. As is shown by theory and illustrated by numerical experiments, the integrator enjoys robustness properties that are not shared by any standard numerical integrator. This robustness can be exploited to change the rank adaptively. Another application is in optimization algorithms for low-rank matrices where truncation back to the given low rank can be done efficiently by applying a step of the integrator proposed here.

The high-temperature series expansion for quantum spin models is a well-established tool to compute thermodynamic quantities and equal-time spin correlations, in particular for frustrated interactions. We extend the scope of this expansion to the dynamic Matsubara spin-spin correlator and develop a fully analytic algorithm to compute its expansion coefficients. We focus on Heisenberg models with a single coupling constant J and spin lengths S=1/2,1. The expansion coefficients up to 12th order in J/T are precomputed on all possible ~10^6 graphs embeddable in arbitrary lattices and are provided under this https URL. This enables calculation of static momentum-resolved susceptibilities for arbitrary site-pairs or wavevectors. We test our results for the S=1/2 Heisenberg chain and on the triangular lattice model. Moreover, the analytic frequency dependence in the expansion allows for stable analytic continuation to the real-frequency dynamic structure factor. This important application is discussed in a companion letter.

The developments over the last five decades concerning numerical discretisations of the incompressible Navier--Stokes equations have lead to reliable tools for their approximation: those include stable methods to properly address the incompressibility constraint, stable discretisations to account for convection dominated problems, efficient time (splitting) methods, and methods to tackle their nonlinear character. While these tools may successfully be applied to reliably simulate even more complex fluid flow PDE models, their understanding requires a fundamental revision in the case of stochastic fluid models, which are gaining increased importance nowadays. This work motivates and surveys optimally convergent numerical methods for the stochastic Stokes and Navier--Stokes equations that were obtained in the last decades. Furtheremore, we computationally illustrate the failure of some of those methods from the deterministic setting, if they are straight-forwardly applied to the stochastic case. In fact, we explain why some of these deterministic methods perform sub-optimally by highlighting crucial analytical differences between the deterministic and stochastic equations -- and how modifications of the deterministic methods restore their optimal performance if they properly address the probabilistic nature of the stochastic problem. Next to the numerical analysis of schemes, we propose a general benchmark of prototypic fluid flow problems driven by different types of noise to also compare new algorithms by simulations in terms of complexities, efficiencies, and possible limitations. The driving motivation is to reach a better comparison of simulations for new schemes in terms of accuracy and complexities, and to also complement theoretical performance studies for restricted settings of data by more realistic ones.

This report documents the programme and the outcomes of Dagstuhl Seminar 22382 "Machine Learning for Science: Bridging Data-Driven and Mechanistic Modelling". Today's scientific challenges are characterised by complexity. Interconnected natural, technological, and human systems are influenced by forces acting across time- and spatial-scales, resulting in complex interactions and emergent behaviours. Understanding these phenomena -- and leveraging scientific advances to deliver innovative solutions to improve society's health, wealth, and well-being -- requires new ways of analysing complex systems. The transformative potential of AI stems from its widespread applicability across disciplines, and will only be achieved through integration across research domains. AI for science is a rendezvous point. It brings together expertise from $\mathrm{AI}$ and application domains; combines modelling knowledge with engineering know-how; and relies on collaboration across disciplines and between humans and machines. Alongside technical advances, the next wave of progress in the field will come from building a community of machine learning researchers, domain experts, citizen scientists, and engineers working together to design and deploy effective AI tools. This report summarises the discussions from the seminar and provides a roadmap to suggest how different communities can collaborate to deliver a new wave of progress in AI and its application for scientific discovery.

In the vicinity of a phase transition ergodicity can be broken. Here, different initial many-body configurations evolve towards one of several fixed points, which are macroscopically distinguishable through an order parameter. This mechanism enables state classification in quantum cellular automata and feed-forward quantum neural networks. We demonstrate that this capability can be efficiently learned from training data even in extremely high-dimensional state spaces. We illustrate this using a quantum cellular automaton that allows binary classification, which is closely connected to the dynamics of a $\mathbb{Z}_2$-symmetric Ising model with local interactions and dissipation. This approach can be generalized beyond binary classification and offers a natural framework for exploring the link between emergent many-body phenomena and the interpretation of data processing capabilities in the context of quantum machine learning.

Axion-like particles (ALPs) are compelling candidates for dark matter and potential portals to new physics beyond the Standard Model. Photons traversing magnetized regions can convert into ALPs, producing characteristic, energy-dependent absorption features in astrophysical spectra. The probability of such conversions depends sensitively on both the photon energy and the properties of the intervening magnetic fields. Most existing searches have focused on individual astrophysical sources, but uncertainties in the structure and strength of cosmic magnetic fields have limited their reach. Recently, we have demonstrated that active galactic nuclei (AGNs) observed through galaxy clusters provide especially promising targets for ALP searches. By stacking multiple AGN-cluster sightlines, one can average over poorly known magnetic field configurations in galaxy clusters and recover a distinctive ALP-induced spectral suppression, thereby significantly enhancing sensitivity. In this work, we investigate a possible systematic uncertainty in such analyses: the intrinsic time-variability of AGN spectra. We demonstrate that AGN flux variability is correlated with spectral hardness, and that time-averaging over flaring and quiescent states can potentially mimic the suppression features imprinted by ALP-photon mixing. Our findings imply that the recent constraints remain conservative, and that incorporating detailed spectral variability into stacking analyses can further sharpen the search for axion-like particles.

Bayesian networks and causal models provide frameworks for handling queries about external interventions and counterfactuals, enabling tasks that go beyond what probability distributions alone can address. While these formalisms are often informally described as capturing causal knowledge, there is a lack of a formal theory characterizing the type of knowledge required to predict the effects of external interventions. This work introduces the theoretical framework of causal systems to clarify Aristotle's distinction between knowledge that and knowledge why within artificial intelligence. By interpreting existing artificial intelligence technologies as causal systems, it investigates the corresponding types of knowledge. Furthermore, it argues that predicting the effects of external interventions is feasible only with knowledge why, providing a more precise understanding of the knowledge necessary for such tasks.

Computing the numerical solution to high-dimensional tensor differential equations can lead to prohibitive computational costs and memory requirements. To reduce the memory and computational footprint, dynamical low-rank approximation (DLRA) has proven to be a promising approach. DLRA represents the solution as a low-rank tensor factorization and evolves the resulting low-rank factors in time. A central challenge in DLRA is to find time integration schemes that are robust to the arising small singular values. A robust parallel basis update & Galerkin integrator, which simultaneously evolves all low-rank factors, has recently been derived for matrix differential equations. This work extends the parallel low-rank matrix integrator to Tucker tensors and general tree tensor networks, yielding an algorithm in which all bases and connecting tensors are evolved in parallel over a time step. We formulate the algorithm, provide a robust error bound, and demonstrate the efficiency of the new integrators for problems in quantum many-body physics, uncertainty quantification, and radiative transfer.

Recent techniques for real-time view synthesis have rapidly advanced in fidelity and speed, and modern methods are capable of rendering near-photorealistic scenes at interactive frame rates. At the same time, a tension has arisen between explicit scene representations amenable to rasterization and neural fields built on ray marching, with state-of-the-art instances of the latter surpassing the former in quality while being prohibitively expensive for real-time applications. In this work, we introduce SMERF, a view synthesis approach that achieves state-of-the-art accuracy among real-time methods on large scenes with footprints up to 300 m$^2$ at a volumetric resolution of 3.5 mm$^3$. Our method is built upon two primary contributions: a hierarchical model partitioning scheme, which increases model capacity while constraining compute and memory consumption, and a distillation training strategy that simultaneously yields high fidelity and internal consistency. Our approach enables full six degrees of freedom (6DOF) navigation within a web browser and renders in real-time on commodity smartphones and laptops. Extensive experiments show that our method exceeds the current state-of-the-art in real-time novel view synthesis by 0.78 dB on standard benchmarks and 1.78 dB on large scenes, renders frames three orders of magnitude faster than state-of-the-art radiance field models, and achieves real-time performance across a wide variety of commodity devices, including smartphones. We encourage readers to explore these models interactively at our project website: this https URL.

Distributionally robust optimization tackles out-of-sample issues like overfitting and distribution shifts by adopting an adversarial approach over a range of possible data distributions, known as the ambiguity set. To balance conservatism and accuracy, these sets must include realistic probability distributions by leveraging information from the nominal distribution. Assuming that nominal distributions arise from a structural causal model with a directed acyclic graph $\mathcal{G}$ and structural equations, previous methods such as adapted and $\mathcal{G}$-causal optimal transport have only utilized causal graph information in designing ambiguity sets. In this work, we propose incorporating structural equations, which include causal graph information, to enhance ambiguity sets, resulting in more realistic distributions. We introduce structural causal optimal transport and its associated ambiguity set, demonstrating their advantages and connections to previous methods. A key benefit of our approach is a relaxed version, where a regularization term replaces the complex causal constraints, enabling an efficient algorithm via difference-of-convex programming to solve structural causal optimal transport. We also show that when structural information is absent and must be estimated, our approach remains effective and provides finite sample guarantees. Lastly, we address the radius of ambiguity sets, illustrating how our method overcomes the curse of dimensionality in optimal transport problems, achieving faster shrinkage with dimension-free order.

We consider the locality and spectral properties of the smearing $$\tau_f(A) = \int_{-\infty}^\infty dt \, f(t) \, \tau_t(A)$$ when applied to the dynamics $\tau_t$ of quantum spin systems. While recent applications of this map have used superpolynomially but not exponentially decaying functions $f$ to ensure exact spectral properties, we use here Gaussian filters. This improves the locality at the expense of errors on the spectral side. We propose a number of concrete applications, from quasi-adiabatic continuation to correlation decay, and exponential stability away from impurities. Finally, we discuss an application to the quantum Hall effect.

Magic trapping of ground and Rydberg states, which equalizes the AC Stark shifts of these two levels, enables increased ground-to-Rydberg state coherence times. We measure via photon storage and retrieval how the ground-to-Rydberg state coherence depends on trap wavelength for two different traps and find different optimal wavelengths for a one-dimensional optical lattice trap and a running wave optical dipole trap. Comparison to theory reveals that this is caused by the Rydberg electron sampling different potential landscapes. The observed difference increases for higher principal quantum numbers, where the extent of the Rydberg electron wave function becomes larger than the optical lattice period. Our analysis shows that optimal magic trapping conditions depend on the trap geometry, in particular for optical lattices and tweezers.

We investigate the energy-energy correlator (EEC) of hadrons produced on the same side in $e^+e^-$ annihilation or in leading jets in $pp$ collisions. We observe a remarkable universality of the correlator. Using a non-perturbative transverse momentum dependent (TMD) fragmentation function to model the transition from the ``free-hadron" region to the perturbative collinear region, we are able to describe the near-side shapes and peaks over a wide range of energy for both the $e^+e^-$ annihilation and the $pp$ jet substructure measurements in terms of just two parameters. We present further predictions for the ratio of the projected three-point energy correlator to the EEC. The excellent agreement between our calculations and the experimental data may provide new insights into the role of non-perturbative physics for EECs, and suggests the possibility of exploring non-perturbative TMDs using theoretical tools developed for the energy correlators.

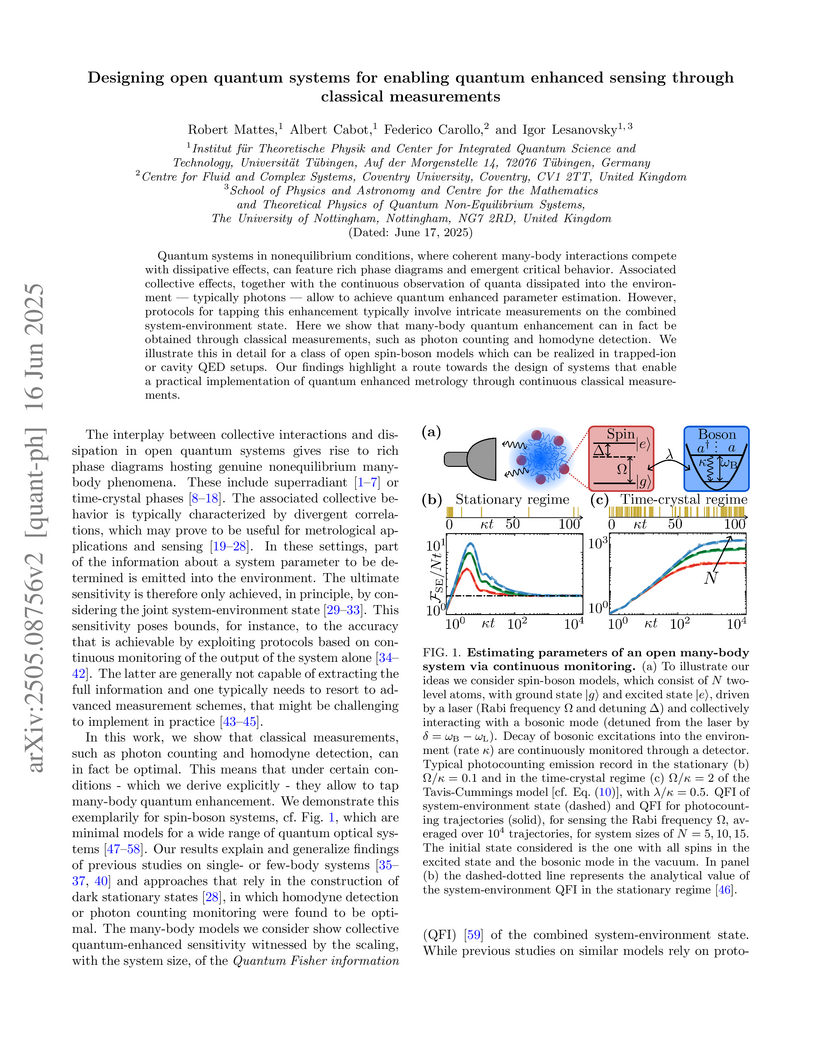
Quantum systems in nonequilibrium conditions, where coherent many-body interactions compete with dissipative effects, can feature rich phase diagrams and emergent critical behavior. Associated collective effects, together with the continuous observation of quanta dissipated into the environment -- typically photons -- allow to achieve quantum enhanced parameter estimation. However, protocols for tapping this enhancement typically involve intricate measurements on the combined system-environment state. Here we show that many-body quantum enhancement can in fact be obtained through classical measurements, such as photon counting and homodyne detection. We illustrate this in detail for a class of open spin-boson models which can be realized in trapped-ion or cavity QED setups. Our findings highlight a route towards the design of systems that enable a practical implementation of quantum enhanced metrology through continuous classical measurements.

We introduce a notion of a \emph{local gap} for interacting many-body quantum lattice systems and prove the validity of response theory and Kubo's formula for localized perturbations in such settings. On a high level, our result shows that the usual spectral gap condition, concerning the system as a whole, is not a necessary condition for understanding local properties of the system. More precisely, we say that an equilibrium state $\rho_0$ of a Hamiltonian $H_0$ is locally gapped in $\Lambda^{\mathrm{gap}} \subset \Lambda$, whenever the Liouvillian $- \mathrm{i} \, [H_0, \, \cdot \, ]$ is almost invertible on local observables supported in $\Lambda^{\mathrm{gap}}$ when tested in $\rho_0$. To put this into context, we provide other alternative notions of a local gap and discuss their relations. The validity of response theory is based on the construction of \emph{non-equilibrium almost stationary states} (NEASSs). By controlling locality properties of the NEASS construction, we show that response theory holds to any order, whenever the perturbation $\epsilon V$ acts in a region which is further than $|\log \epsilon|$ away from the non-gapped region $\Lambda \setminus \Lambda^{\mathrm{gap}}$.

Trapped ions are among the most advanced platforms for quantum simulation and computation. Their capabilities can be further augmented by making use of electronically highly excited Rydberg states, which enable the realization of long-ranged electric dipolar interactions. Most experimental and theoretical studies so far focus on the excitation of ionic Rydberg states in linear Paul traps, which generate confinement by a combination of static and oscillating electric fields. These two fields need to be carefully aligned to minimize so-called micromotion, caused by the time-dependent electric field. The purpose of this work is to systematically understand the qualitative impact of micromotion on the Rydberg excitation spectrum, when the symmetry axes of the two electric fields do not coincide. Considering this scenario is not only important in the case of possible field misalignment, but becomes inevitable for Rydberg excitations in 2D and 3D ion crystals. We develop a minimal model describing a single trapped Rydberg ion, which we solve numerically via Floquet theory and analytically using a perturbative approach. We calculate the excitation spectra and analyze in which parameter regimes addressable and energetically isolated Rydberg lines persist, which are an important requirement for conducting coherent manipulations.

Open many-body quantum systems can exhibit intriguing nonequilibrium phases of matter, such as time crystals. In these phases, the state of the system spontaneously breaks the time-translation symmetry of the dynamical generator, which typically manifests through persistent oscillations of an order parameter. A paradigmatic model displaying such a symmetry breaking is the boundary time crystal, which has been extensively analyzed experimentally and theoretically. Despite the broad interest in these nonequilibrium phases, their thermodynamics and their fluctuating behavior remain largely unexplored, in particular for the case of coupled time crystals. In this work, we consider two interacting boundary time crystals and derive a consistent interpretation of their thermodynamic behavior. We fully characterize their average dynamics and the behavior of their quantum fluctuations, which allows us to demonstrate the presence of quantum and classical correlations in both the stationary and the time-crystal phases displayed by the system. We furthermore exploit our theoretical derivation to explore possible applications of time crystals as quantum batteries, demonstrating their ability to efficiently store energy.