Computer Vision (CV)-based continuous, automated and precise salmon welfare monitoring is a key step toward reduced salmon mortality and improved salmon welfare in industrial aquaculture net pens. Available CV methods for determining welfare indicators focus on single indicators and rely on object detectors and trackers from other application areas to aid their welfare indicator calculation algorithm. This comes with a high resource demand for real-world applications, since each indicator must be calculated separately. In addition, the methods are vulnerable to difficulties in underwater salmon scenes, such as object occlusion, similar object appearance, and similar object motion. To address these challenges, we propose a flexible tracking framework that uses a pose estimation network to extract bounding boxes around salmon and their corresponding body parts, and exploits information about the body parts, through specialized modules, to tackle challenges specific to underwater salmon scenes. Subsequently, the high-detail body part tracks are employed to calculate welfare indicators. We construct two novel datasets assessing two salmon tracking challenges: salmon ID transfers in crowded scenes and salmon ID switches during turning. Our method outperforms the current state-of-the-art pedestrian tracker, BoostTrack, for both salmon tracking challenges. Additionally, we create a dataset for calculating salmon tail beat wavelength, demonstrating that our body part tracking method is well-suited for automated welfare monitoring based on tail beat analysis. Datasets and code are available at this https URL.

This paper presents a dataset gathered with an underwater robot in a sea-based aquaculture setting. Data was gathered from an operational fish farm and includes data from sensors such as the Waterlinked A50 DVL, the Nortek Nucleus 1000 DVL, Sonardyne Micro Ranger 2 USBL, Sonoptix Mulitbeam Sonar, mono and stereo cameras, and vehicle sensor data such as power usage, IMU, pressure, temperature, and more. Data acquisition is performed during both manual and autonomous traversal of the net pen structure. The collected vision data is of undamaged nets with some fish and marine growth presence, and it is expected that both the research community and the aquaculture industry will benefit greatly from the utilization of the proposed SOLAQUA dataset.

Small lightweight wave buoys, SFYs, designed to operate near the coast, have been developed. The buoys are designed to record and transmit the full time series of surface acceleration at $52$ Hz. The buoy uses the cellular network to transfer data and position (up to $80$ km from the base station). This reduces costs and increases band-width. The low cost and low weight permits the buoys to be deployed easily, and in arrays in areas where satellite and wave models struggle to resolve wave and current interaction. The buoys are tested in a wave-flume, the open water and in the breaking waves of the surf. The conditions range from calm to significant wave heights exceeding $7$ m and crashing breakers with accelerations exceeding $10$ g. The high sample rate captures the impulse of breaking waves, and allows them to be studied in detail. Breaking waves are measured and quantified in the open water. We measure breaking waves in the surf and recover the trajectory of waves breaking in the field to a higher degree than previously done. The time series of surface elevation, and accurate positioning, permits the signal of adjacent buoys to be correlated in a coherent phase-resolved way. Finally, we offer an explanation and solution for the ubiquitous low-frequency noise in IMU-based buoys and discuss necessary sampling and design to measure in areas of breaking waves.

Autonomous navigation in 3D is a fundamental problem for autonomy. Despite major advancements in terrestrial and aerial settings due to improved range sensors including LiDAR, compact sensors with similar capabilities for underwater robots have only recently become available, in the form of 3D sonars. This paper introduces a novel underwater 3D navigation pipeline, called SHRUMS (Sensor Hallucination for Robust Underwater Motion planning with 3D Sonar). To the best of the authors' knowledge, SHRUMS is the first underwater autonomous navigation stack to integrate a 3D sonar. The proposed pipeline exhibits strong robustness while operating in complex 3D environments in spite of extremely poor visibility conditions. To accommodate the intricacies of the novel sensor data stream while achieving real-time locally optimal performance, SHRUMS introduces the concept of hallucinating sensor measurements from non-existent sensors with convenient arbitrary parameters, tailored to application specific requirements. The proposed concepts are validated with real 3D sonar sensor data, utilizing real inputs in challenging settings and local maps constructed in real-time. Field deployments validating the proposed approach in full are planned in the very near future.

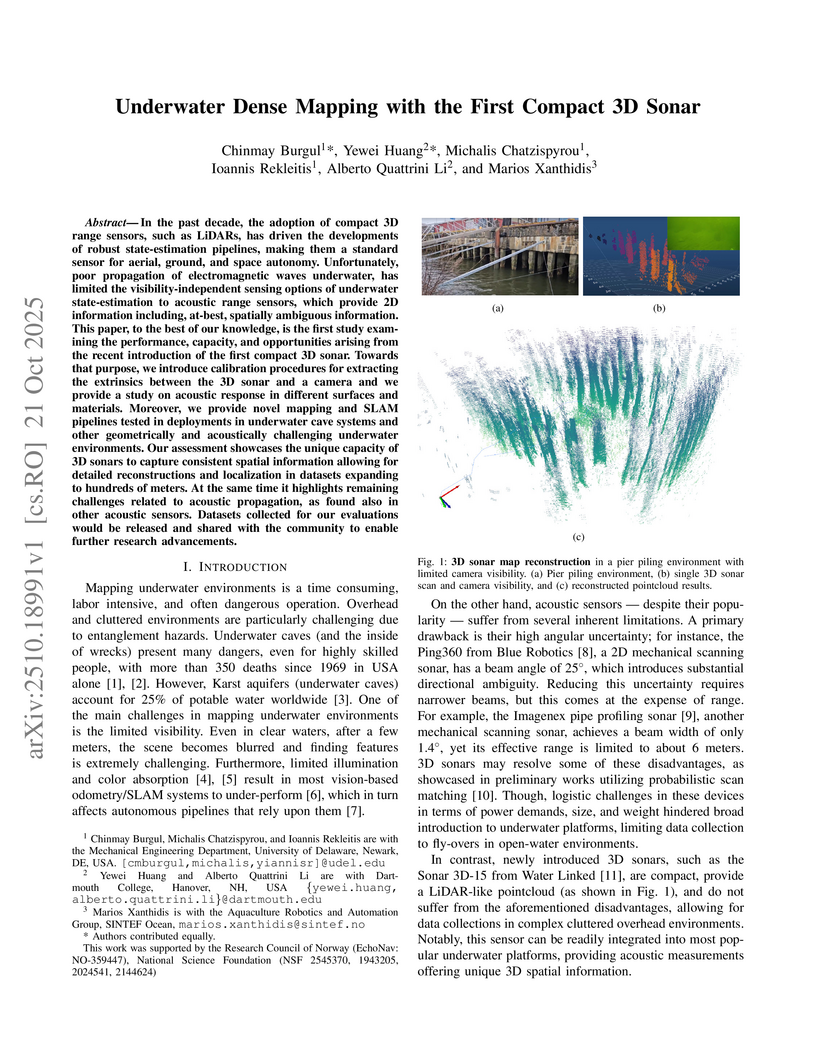
In the past decade, the adoption of compact 3D range sensors, such as LiDARs, has driven the developments of robust state-estimation pipelines, making them a standard sensor for aerial, ground, and space autonomy. Unfortunately, poor propagation of electromagnetic waves underwater, has limited the visibility-independent sensing options of underwater state-estimation to acoustic range sensors, which provide 2D information including, at-best, spatially ambiguous information. This paper, to the best of our knowledge, is the first study examining the performance, capacity, and opportunities arising from the recent introduction of the first compact 3D sonar. Towards that purpose, we introduce calibration procedures for extracting the extrinsics between the 3D sonar and a camera and we provide a study on acoustic response in different surfaces and materials. Moreover, we provide novel mapping and SLAM pipelines tested in deployments in underwater cave systems and other geometrically and acoustically challenging underwater environments. Our assessment showcases the unique capacity of 3D sonars to capture consistent spatial information allowing for detailed reconstructions and localization in datasets expanding to hundreds of meters. At the same time it highlights remaining challenges related to acoustic propagation, as found also in other acoustic sensors. Datasets collected for our evaluations would be released and shared with the community to enable further research advancements.

As the global population grows and climate change intensifies, sustainable food production is critical. Marine aquaculture offers a viable solution, providing a sustainable protein source. However, the industry's expansion requires novel technologies for remote management and autonomous operations. Digital twin technology can advance the aquaculture industry, but its adoption has been limited. Fish net cages, which are flexible floating structures, are critical yet vulnerable components of aquaculture farms. Exposed to harsh and dynamic marine environments, the cages experience significant loads and risk damage, leading to fish escapes, environmental impacts, and financial losses. We propose a multifidelity surrogate modeling framework for integration into a digital twin for real-time monitoring of aquaculture net cage structural dynamics under stochastic marine conditions. Central to this framework is the nonlinear autoregressive Gaussian process method, which learns complex, nonlinear cross-correlations between models of varying fidelity. It combines low-fidelity simulation data with a small set of high-fidelity field sensor measurements, which offer the real dynamics but are costly and spatially sparse. Validated at the SINTEF ACE fish farm in Norway, our digital twin receives online metocean data and accurately predicts net cage displacements and mooring line loads, aligning closely with field measurements. The proposed framework is beneficial where application-specific data are scarce, offering rapid predictions and real-time system representation. The developed digital twin prevents potential damages by assessing structural integrity and facilitates remote operations with unmanned underwater vehicles. Our work also compares GP and GCNs for predicting net cage deformation, highlighting the latter's effectiveness in complex structural applications.

Here, we present the concept of an open virtual prototyping framework for maritime systems and operations that enables its users to develop re-usable component or subsystem models, and combine them in full-system simulations for prototyping, verification, training, and performance studies. This framework consists of a set of guidelines for model coupling, high-level and low-level coupling interfaces to guarantee interoperability, a full-system simulation software, and example models and demonstrators. We discuss the requirements for such a framework, address the challenges and the possibilities in fulfilling them, and aim to give a list of best practices for modular and efficient virtual prototyping and full-system simulation. The context of our work is within maritime systems and operations, but the issues and solutions we present here are general enough to be of interest to a much broader audience, both industrial and scientific.

Slender marine structures such as deep-water riser systems are continuously exposed to currents leading to vortex-induced vibrations (VIV) of the structure. This may result in amplified drag loads and fast accumulation of fatigue damage. Consequently, accurate prediction of VIV responses is of great importance for the safe design and operation of marine risers. Model tests with elastic pipes have shown that VIV responses are influenced by many structural and hydrodynamic parameters, which have not been fully modelled in present frequency domain VIV prediction tools. Traditionally, predictions have been computed using a single set of hydrodynamic parameters, often leading to inconsistent prediction accuracy when compared with observed field measurements and experimental data. Hence, it is necessary to implement a high safety factor of 10 - 20 in the riser design, which increases development cost and adds extra constraints in the field operation. One way to compensate for the simplifications in the mathematical prediction model is to apply adaptive parameters to describe different riser responses. The objective of this work is to demonstrate a new method to improve the prediction consistency and accuracy by applying adaptive hydrodynamic parameters. In the present work, a four-step approach has been proposed: First, the measured VIV response will be analysed to identify key parameters to represent the response characteristics. These parameters will be grouped using data clustering algorithms. Secondly, optimal hydrodynamic parameters will be identified for each data group by optimisation against measured data. Thirdly, the VIV response using the obtained parameters will be calculated and the prediction accuracy evaluated. The correct hydrodynamic parameters to be used for new cases can be obtained from the clustering. This concept has been demonstrated with examples from experimental data.

Simulating oil transport in the ocean can be done successfully provided that accurate ocean currents and surface winds are available -- this is often too big of a challenge. Deficient ocean currents can sometimes be remediated by parameterizing missing physics -- this is often not enough. In this chapter, we focus on some of the main problems oil-spill modelers face, which is determining accurate trajectories when the velocity may be missing important physics, or when the velocity has localized errors that result in large trajectory errors. A foundation of physical mechanisms driving motion in the ocean may help identify currents lacking certain types of physics, and the remedy. Recent progress in our understanding of motion in the upper centimeters of the ocean supports unconventional parameterizations; we present as an example the 2003 Point Wells oil spill which had remained unexplained until recently. When the velocity realistically represents trajectory forcing mechanisms, advanced Lagrangian techniques that build on the theory of Lagrangian Coherent Structures can bypass localized velocity errors by identifying regions of attraction likely to dictate fluid deformation. The usefulness of Objective Eulerian Coherent Structures is demonstrated to the oil-spill modeling community by revisiting the 2010 Deepwater Horizon accident in the Gulf of Mexico and predicting a prominent transport pattern from an imperfect altimetry velocity eight days in advance.

We present direct numerical simulation of a mechanism for creating longitudinal vortices in pipe flow, compared with a simple model theory. By furnishing the pipe wall with a pattern of crossing waves secondary flow in the form of spanwise vortex pairs is created. The mechanism `CL1' is kinematic and known from oceanography as a driver of Langmuir circulation. CL1 is strongest when the `wall wave' vectors make an accute angle with the axis, $\varphi=10^\circ$ - $20^\circ$ (a `contracted eggcarton'), changes sign near $45^\circ$ and is weak and opposite beyond this angle. A competing, dynamic mechanism driving secondary flow in the opposite sense is also observed created by the azimuthally varying friction. Whereas at smaller angles `CL1' prevails, the dynamic effect dominates when $\varphi\gtrsim 45^\circ$ reversing the flow. Curiously, circulation strength is a faster-than-linearly increasing function of Reynolds number for the contracted case. We explore an analogy with Prandtl's secondary motion of the second kind in turbulence. A transport equation for average streamwise vorticity is derived, and we analyse it for three different crossing angles, $\varphi=18.6^\circ, 45^\circ$and$60^\circ$. Mean-vorticity production is organised in a ring-like structure with the two rings contributing to rotating flow in opposite senses. For the larger $\varphi$ the inner ring decides the main swirling motion, whereas for $\varphi=18.6^\circ$ outer-ring production dominates. For the larger angles the outer ring is mainly driven by advection of vorticity and the inner by deformation (stretching) whereas for $\varphi=18.6^\circ$ both contribute approximately equally to production in the outer ring.

Air-sea exchange processes have been identified as essential for both short- and long-term atmospheric and ocean forecasts. The two phases of the fluid layer covering our planet interact across a vast range of scales that we need to explore to achieve a better understanding of the exchange processes. While satellites provide a distributed large-scale view of the sea surface situation, highly detailed measurements, e.g., from oceanographic towers, are necessarily local. The required intermediate solution (i.e., data that are both accurate and distributed) can be provided by swarms of miniature surface buoys. As size, weight, and cost are reduced, these can be deployed in large numbers to investigate specific processes that are at present only crudely parameterized in our models as a result of scarcity of good measurements. Perhaps the most crucial process is white-capping in stormy conditions, where air-sea exchanges are enhanced by one or two orders of magnitude. Other applications include wave-current interactions, wave-ice interactions, and plunging breakers in the coastal zone. Following a dedicated workshop, we summarize here the main findings and possibilities derived from the different approaches, and summarize the state of the art for a selection of miniature buoys. We list the solutions presented at the workshop, as well as other similar buoys, with their main characteristics and range of application. We describe the various possibilities of practical use and the scientific and engineering problems to be solved. Looking to the future, we also point out where the present technological improvements are leading to.

Offshore slender marine structures experience complex and combined load conditions from waves, current and vessel motions that may result in both wave frequency and vortex shedding response patterns. Field measurements often consist of records of environmental conditions and riser responses, typically with 30-minute intervals. These data can be represented in a high-dimensional parameter space. However, it is difficult to visualize and understand the structural responses, as they are affected by many of these parameters. It becomes easier to identify trends and key parameters if the measurements with the same characteristics can be grouped together. Cluster analysis is an unsupervised learning method, which groups the data based on their relative distance, density of the data space, intervals, or statistical distributions. In the present study, a Gaussian mixture model guided by domain knowledge has been applied to analyze field measurements. Using the 242 measurement events of the Helland-Hansen riser, it is demonstrated that riser responses can be grouped into 12 clusters by the identification of key environmental parameters. This results in an improved understanding of complex structure responses. Furthermore, the cluster results are valuable for evaluating the riser response prediction accuracy.

Aquaculture is a big marine industry and contributes to securing global food demands. Underwater vehicles such as remotely operated vehicles (ROVs) are commonly used for inspection, maintenance, and intervention (IMR) tasks in fish farms. However, underwater vehicle operations in aquaculture face several unique and demanding challenges, such as navigation in dynamically changing environments with time-varying sealoads and poor hydroacoustic sensor capabilities, challenges yet to be properly addressed in research. This paper will present various endeavors to address these questions and improve the overall autonomy level in aquaculture robotics, with a focus on field experiments. We will also discuss lessons learned during field trials and potential future prospects in aquaculture robotics.

Offshore wave studies often assume Gaussian processes and homogeneous wave fields. However, as waves approach the shoreline, complex coastal topo-bathymetry induces transformations such as shoaling, refraction, diffraction, reflection, and breaking, leading to increased nonlinearity and site-specific wave characteristics. This complexity necessitates detailed site-specific studies for coastal infrastructure design and blue economy planning. This work presents a downscaling procedure for analyzing wave-structure interactions from offshore metocean conditions. The open-access NORA3 and NORA10EI hindcast databases define offshore sea states, which are propagated to nearshore regions using the phase-averaged wave model SWAN. The outputs inform phase-resolving simulations with the fully nonlinear potential flow solver REEF3D::FNPF, incorporating an Arbitrary Eulerian-Lagrangian (ALE) method to compute wave forces via Morisons formulation and to screen for extreme events. Extreme wave loads are further examined using the fully viscous Navier-Stokes solver REEF3D::CFD. A one-way hydrodynamic coupling (HDC) between the potential flow and viscous solvers ensures accurate information transfer. The proposed NORA-SARAH framework, integrating NORA databases with SWAN, REEF3D, ALE, and HDC, offers a robust approach for complex coastal environments. A case study in Southern Norway demonstrates its advantages over traditional significant wave height (Hs)-based or phase-averaged modeling practices, highlighting the necessity of this downscaling method.

A two-dimensional water wave model based on conformal mapping is presented. The model is exact in the sense that it does not rely on truncated series expansions, nor suffer any numerical diffusion. Additionally, it is computationally highly efficient as it numerically evaluates only the surface line while using a fixed number of FFT operations per time step. A double layered mapping enforces prescribed outer boundaries without iteration. The model also supports transient boundaries, including walls. Mapping models are presented that support smooth bathymetries and angled overhanging geometries. An exact piston-type wavemaker model demonstrates the method's potential as a numerical wave tank. The model is tested and validated through a number of examples covering shallow water waves, wavemaker generation, rising bathymetry shelves, and wave reflection from slanting structures. A paddle-type wavemaker model, developed from the present theory, will be detailed in a forthcoming paper.

The second-order directional wavemaker theory for regular and irregular waves is extended to multi-hinged wavemakers and combined piston--flap wavemaker systems. Derived expressions enable second-order signal correction, common in single-hinged wavemakers, to be applied to multi-hinged systems. Multi-hinged wavemakers offer additional degrees of freedom, with different combinations of paddle motion producing the same progressive wave. This is here exploited to better understand wavemaker behaviour. Single-harmonic signals are computed for double-hinged wavemakers that suppress spurious waves without introducing double-harmonic motions. Surprisingly, these flap motions are almost always in opposite phase, with the larger draft found underneath the water surface. %contradicting to assumptions from earlier studies. Due to the opposing paddle phase, the double-hinged wavemaker draft is usually smaller than the corresponding single-hinged draft. The ability of thsee systems to suppress spurious waves with single-harmonic motion is verified experimentally. The wavemaker theory further supports an arbitrary number of flap hinges, enabling the approximation of a fully flexible wavemaker through piecewise-linear segments. This is demonstrated with an exponential wavemaker profile that does not generate any evanescent waves at linear order. Such a wavemaker is likely to limit wave breaking and cross-modes, but is found to produce spurious second-order waves of a magnitude comparable to a single flap. The presented solution is complete, intrinsically including return flow through the second-order zero mode. This return flow is found to precisely match the Stokes drift.

In this work, we present a boundary and hole detection approach that traverses all the boundaries of an edge-manifold triangular mesh, irrespectively of the presence of singular vertices, and subsequently determines and labels all holes of the mesh. The proposed automated hole-detection method is valuable to the computer-aided design (CAD) community as all half-edges within the mesh are utilized and for each half-edge the algorithm guarantees both the existence and the uniqueness of the boundary associated to it. As existing hole-detection approaches assume that singular vertices are absent or may require mesh modification, these methods are ill-equipped to detect boundaries/holes in real-world meshes that contain singular vertices. We demonstrate the method in an underwater autonomous robotic application, exploiting surface reconstruction methods based on point cloud data. In such a scenario the determined holes can be interpreted as information gaps, enabling timely corrective action during the data acquisition. However, the scope of our method is not confined to these two sectors alone; it is versatile enough to be applied on any edge-manifold triangle mesh. An evaluation of the method is performed on both synthetic and real-world data (including a triangle mesh from a point cloud obtained by a multibeam sonar). The source code of our reference implementation is available: this https URL

We report experimental evidence of an Eulerian-mean flow, $\overline{u}(z)$, created by the interaction of surface waves and tailored ambient sub-surface turbulence, which partly cancels the Stokes drift, $u_s(z)$, and present supporting theory. Water-side turbulent velocity fields and Eulerian-mean flows were measured with particle image velocimetry before vs after the passage of a wave group, and with vs without the presence of regular waves. We compare different wavelengths, steepnesses and turbulent intensities. In all cases, a significant change in the Eulerian-mean current is observed, strongly focused near the surface, where it opposes the Stokes drift. The observations support the picture that when waves encounter ambient sub-surface turbulence, the flow undergoes a transition during which Eulerian-mean momentum is redistributed vertically (without changing the depth-integrated mass transport) until a new equilibrium state is reached, wherein the near-surface ratio between $\mathrm{d}\overline{u}/\mathrm{d}z$ and $|\mathrm{d}u_s/\mathrm{d} z|$ approximately equals the ratio between the streamwise and vertical Reynolds normal stresses. This accords with a simple statistical theory derived here and holds regardless of the absolute turbulence level, whereas stronger turbulence means faster growth of the Eulerian-mean current. We present a model based on Rapid Distortion Theory which describes the generation of the Eulerian-mean flow as a consequence of the action of the Stokes drift on the background turbulence. Predictions are in qualitative, and reasonable quantitative, agreement with experiments on wave groups, where equilibrium has not yet been reached. Our results could have substantial consequences for predicting the transport of water-borne material in the oceans.

Subsea umbilical and power cables contain a large number of contact interfaces between different geometries and materials. These complex interactions rise significant challenges for accurately considering contact surface properties by using traditional analytical solutions or finite element methods. These properties have been identified as the most sensitive parameters when performing the numerical simulation for stress analysis. Therefore, it is essential to apply a novel approach for contact analysis which improves the accuracy and efficiency for predicting contact properties. This paper presents an isogeometric analysis (IGA) approach addressing contact problems in dynamic umbilicals and power cables. Firstly, this isogeometric contact algorithm is formulated in MATLAB as a tool including the geometry description, contact detection and penalty function. Secondly, the contact interface between a steel tube and an outer sheath in an dynamic umbilical is established by this IGA contact algorithm and validated against that in ABAQUS for proving the accuracy and efficiency of IGA. Finally, the effects of element refinement, geometrical description, penalty factor on the accuracy, efficiency and stability of IGA are discussed.

We review error estimation methods for co-simulation, in particular methods that are applicable when the subsystems provide minimal interfaces. By this, we mean that subsystems do not support rollback of time steps, do not output derivatives, and do not provide any other information about their internals other than the output variables that are required for coupling with other subsystems. Such "black-box" subsystems are quite common in industrial applications, and the ability to couple them and run large-system simulations is one of the major attractions of the co-simulation paradigm. We also describe how the resulting error indicators may be used to automatically control macro time step sizes in order to strike a good balance between simulation speed and accuracy. The various elements of the step size control algorithm are presented in pseudocode so that readers may implement them and test them in their own applications. We provide practicable advice on how to use error indicators to judge the quality of a co-simulation, how to avoid common pitfalls, and how to configure the step size control algorithm.