Autoregressive models are typically applied to sequences of discrete tokens, but recent research indicates that generating sequences of continuous embeddings in an autoregressive manner is also feasible. However, such Continuous Autoregressive Models (CAMs) can suffer from a decline in generation quality over extended sequences due to error accumulation during inference. We introduce a novel method to address this issue by injecting random noise into the input embeddings during training. This procedure makes the model robust against varying error levels at inference. We further reduce error accumulation through an inference procedure that introduces low-level noise. Experiments on musical audio generation show that CAM substantially outperforms existing autoregressive and non-autoregressive approaches while preserving audio quality over extended sequences. This work paves the way for generating continuous embeddings in a purely autoregressive setting, opening new possibilities for real-time and interactive generative applications.

Proximity-based cities have attracted much attention in recent years. The 15-minute city, in particular, heralded a new vision for cities where essential services must be easily accessible. Despite its undoubted merit in stimulating discussion on new organisations of cities, the 15-minute city cannot be applicable everywhere, and its very definition raises a few concerns. Here, we tackle the feasibility and practicability of the '15-minute city' model in many cities worldwide. We provide a worldwide quantification of how close cities are to the ideal of the 15-minute city. To this end, we measure the accessibility times to resources and services, and we reveal strong heterogeneity of accessibility within and across cities, with a significant role played by local population densities. We provide an online platform (\href{whatif.sonycsl.it/15mincity}{whatif.sonycsl.it/15mincity}) to access and visualise accessibility scores for virtually all cities worldwide. The heterogeneity of accessibility within cities is one of the sources of inequality. We thus simulate how much a better redistribution of resources and services could heal inequity by keeping the same resources and services or by allowing for virtually infinite resources. We highlight pronounced discrepancies among cities in the minimum number of additional services needed to comply with the 15-minute city concept. We conclude that the proximity-based paradigm must be generalised to work on a wide range of local population densities. Finally, socio-economic and cultural factors should be included to shift from time-based to value-based cities.

Luminescence imaging is invaluable for studying biological and material systems, particularly when advanced protocols that exploit temporal dynamics are employed. However, implementing such protocols often requires custom instrumentation, either modified commercial systems or fully bespoke setups, which poses a barrier for researchers without expertise in optics, electronics, or software. To address this, we present a versatile macroscopic fluorescence imaging system capable of supporting a wide range of protocols, and provide detailed build instructions along with open-source software to enable replication with minimal prior experience. We demonstrate its broad utility through applications to plants, reversibly photoswitchable fluorescent proteins, and optoelectronic devices.

Recent advancements in deep generative models present new opportunities for music production but also pose challenges, such as high computational demands and limited audio quality. Moreover, current systems frequently rely solely on text input and typically focus on producing complete musical pieces, which is incompatible with existing workflows in music production. To address these issues, we introduce "Diff-A-Riff," a Latent Diffusion Model designed to generate high-quality instrumental accompaniments adaptable to any musical context. This model offers control through either audio references, text prompts, or both, and produces 48kHz pseudo-stereo audio while significantly reducing inference time and memory usage. We demonstrate the model's capabilities through objective metrics and subjective listening tests, with extensive examples available on the accompanying website: sonycslparis.github.io/diffariff-companion/

This work studies the Geometric Jensen-Shannon divergence, based on the notion of geometric mean of probability measures, in the setting of Gaussian measures on an infinite-dimensional Hilbert space. On the set of all Gaussian measures equivalent to a fixed one, we present a closed form expression for this divergence that directly generalizes the finite-dimensional version. Using the notion of Log-Determinant divergences between positive definite unitized trace class operators, we then define a Regularized Geometric Jensen-Shannon divergence that is valid for any pair of Gaussian measures and that recovers the exact Geometric Jensen-Shannon divergence between two equivalent Gaussian measures when the regularization parameter tends to zero.

We describe a framework to build distances by measuring the tightness of inequalities, and introduce the notion of proper statistical divergences and improper pseudo-divergences. We then consider the Hölder ordinary and reverse inequalities, and present two novel classes of Hölder divergences and pseudo-divergences that both encapsulate the special case of the Cauchy-Schwarz divergence. We report closed-form formulas for those statistical dissimilarities when considering distributions belonging to the same exponential family provided that the natural parameter space is a cone (e.g., multivariate Gaussians), or affine (e.g., categorical distributions). Those new classes of Hölder distances are invariant to rescaling, and thus do not require distributions to be normalized. Finally, we show how to compute statistical Hölder centroids with respect to those divergences, and carry out center-based clustering toy experiments on a set of Gaussian distributions that demonstrate empirically that symmetrized Hölder divergences outperform the symmetric Cauchy-Schwarz divergence.

Taking long-term spectral and temporal dependencies into account is essential for automatic piano transcription. This is especially helpful when determining the precise onset and offset for each note in the polyphonic piano content. In this case, we may rely on the capability of self-attention mechanism in Transformers to capture these long-term dependencies in the frequency and time axes. In this work, we propose hFT-Transformer, which is an automatic music transcription method that uses a two-level hierarchical frequency-time Transformer architecture. The first hierarchy includes a convolutional block in the time axis, a Transformer encoder in the frequency axis, and a Transformer decoder that converts the dimension in the frequency axis. The output is then fed into the second hierarchy which consists of another Transformer encoder in the time axis. We evaluated our method with the widely used MAPS and MAESTRO v3.0.0 datasets, and it demonstrated state-of-the-art performance on all the F1-scores of the metrics among Frame, Note, Note with Offset, and Note with Offset and Velocity estimations.

Social dialogue, the foundation of our democracies, is currently threatened by disinformation and partisanship, with their disrupting role on individual and collective awareness and detrimental effects on decision-making processes. Despite a great deal of attention to the news sphere itself, little is known about the subtle interplay between the offer and the demand for information. Still, a broader perspective on the news ecosystem, including both the producers and the consumers of information, is needed to build new tools to assess the health of the infosphere. Here, we combine in the same framework news supply, as mirrored by a fairly complete Italian news database - partially annotated for fake news, and news demand, as captured through the Google Trends data for Italy. Our investigation focuses on the temporal and semantic interplay of news, fake news, and searches in several domains, including the virus SARS-CoV-2 pandemic. Two main results emerge. First, disinformation is extremely reactive to people's interests and tends to thrive, especially when there is a mismatch between what people are interested in and what news outlets provide. Second, a suitably defined index can assess the level of disinformation only based on the available volumes of news and searches. Although our results mainly concern the Coronavirus subject, we provide hints that the same findings can have more general applications. We contend these results can be a powerful asset in informing campaigns against disinformation and providing news outlets and institutions with potentially relevant strategies.

As for many motile micro-algae, the freshwater species Chlamydomonas reinhardtii can detect light sources and adapt its motile behavior in response. Here, we show that suspensions of photophobic cells can be unstable to density fluctuations, as a consequence of shading interactions mediated by light absorption. In a circular illumination geometry this mechanism leads to the complete phase separation of the system into transient branching patterns, providing the first experimental evidence of finite wavelength selection in an active phase-separating system without birth and death processes. The finite wavelength selection, that can be captured in a simple drift-diffusion framework, is a consequence of a vision-based interaction length scale set by the illumination geometry and depends on global cell density, light intensity and medium viscosity. Finally we show that this active phase separation shields individual cells from the deleterious effects of high light intensity, demonstrating that phototaxis can efficiently contribute to photoprotection through collective behaviors on short timescales.

In traditional supervised learning, the cross-entropy loss treats all incorrect predictions equally, ignoring the relevance or proximity of wrong labels to the correct answer. By leveraging a tree hierarchy for fine-grained labels, we investigate hybrid losses, such as generalised triplet and cross-entropy losses, to enforce similarity between labels within a multi-task learning framework. We propose metrics to evaluate the embedding space structure and assess the model's ability to generalise to unseen classes, that is, to infer similar classes for data belonging to unseen categories. Our experiments on OrchideaSOL, a four-level hierarchical instrument sound dataset with nearly 200 detailed categories, demonstrate that the proposed hybrid losses outperform previous works in classification, retrieval, embedding space structure, and generalisation.

The distribution of urban services reveals critical patterns of human activity and accessibility. Proximity to amenities like restaurants, banks, and hospitals can reduce access barriers, but these services are often unevenly distributed, exacerbating spatial inequalities and socioeconomic disparities. In this study, we present a novel accessibility measure based on the spatial distribution of Points of Interest (POIs) within cities. Using the radial distribution function from statistical physics, we analyze the dispersion of services across different urban zones, combining local and remote access to services. This approach allows us to identify a city's central core, intermediate areas or secondary cores, and its periphery. Comparing the areas that we find with the resident population distribution highlights clusters of urban services and helps uncover disparities in access to opportunities.

Psychoacoustical so-called "timbre spaces" map perceptual similarity ratings of instrument sounds onto low-dimensional embeddings via multidimensional scaling, but suffer from scalability issues and are incapable of generalization. Recent results from audio (music and speech) quality assessment as well as image similarity have shown that deep learning is able to produce embeddings that align well with human perception while being largely free from these constraints. Although the existing human-rated timbre similarity data is not large enough to train deep neural networks (2,614 pairwise ratings on 334 audio samples), it can serve as test-only data for audio models. In this paper, we introduce metrics to assess the alignment of diverse audio representations with human judgments of timbre similarity by comparing both the absolute values and the rankings of embedding distances to human similarity ratings. Our evaluation involves three signal-processing-based representations, twelve representations extracted from pre-trained models, and three representations extracted from a novel sound matching model. Among them, the style embeddings inspired by image style transfer, extracted from the CLAP model and the sound matching model, remarkably outperform the others, showing their potential in modeling timbre similarity.

Autoregressive models are now capable of generating high-quality minute-long expressive MIDI piano performances. Even though this progress suggests new tools to assist music composition, we observe that generative algorithms are still not widely used by artists due to the limited control they offer, prohibitive inference times or the lack of integration within musicians' workflows. In this work, we present the Piano Inpainting Application (PIA), a generative model focused on inpainting piano performances, as we believe that this elementary operation (restoring missing parts of a piano performance) encourages human-machine interaction and opens up new ways to approach music composition. Our approach relies on an encoder-decoder Linear Transformer architecture trained on a novel representation for MIDI piano performances termed Structured MIDI Encoding. By uncovering an interesting synergy between Linear Transformers and our inpainting task, we are able to efficiently inpaint contiguous regions of a piano performance, which makes our model suitable for interactive and responsive A.I.-assisted composition. Finally, we introduce our freely-available Ableton Live PIA plugin, which allows musicians to smoothly generate or modify any MIDI clip using PIA within a widely-used professional Digital Audio Workstation.

Recent MIDI-to-audio synthesis methods using deep neural networks have successfully generated high-quality, expressive instrumental tracks. However, these methods require MIDI annotations for supervised training, limiting the diversity of instrument timbres and expression styles in the output. We propose CoSaRef, a MIDI-to-audio synthesis method that does not require MIDI-audio paired datasets. CoSaRef first generates a synthetic audio track using concatenative synthesis based on MIDI input, then refines it with a diffusion-based deep generative model trained on datasets without MIDI annotations. This approach improves the diversity of timbres and expression styles. Additionally, it allows detailed control over timbres and expression through audio sample selection and extra MIDI design, similar to traditional functions in digital audio workstations. Experiments showed that CoSaRef could generate realistic tracks while preserving fine-grained timbre control via one-shot samples. Moreover, despite not being supervised on MIDI annotation, CoSaRef outperformed the state-of-the-art timbre-controllable method based on MIDI supervision in both objective and subjective evaluation.

The $k$-nearest neighbor ($k$-NN) algorithm is one of the most popular methods for nonparametric classification. However, a relevant limitation concerns the definition of the number of neighbors $k$. This parameter exerts a direct impact on several properties of the classifier, such as the bias-variance tradeoff, smoothness of decision boundaries, robustness to noise, and class imbalance handling. In the present paper, we introduce a new adaptive $k$-nearest neighbours ($kK$-NN) algorithm that explores the local curvature at a sample to adaptively defining the neighborhood size. The rationale is that points with low curvature could have larger neighborhoods (locally, the tangent space approximates well the underlying data shape), whereas points with high curvature could have smaller neighborhoods (locally, the tangent space is a loose approximation). We estimate the local Gaussian curvature by computing an approximation to the local shape operator in terms of the local covariance matrix as well as the local Hessian matrix. Results on many real-world datasets indicate that the new $kK$-NN algorithm yields superior balanced accuracy compared to the established $k$-NN method and also another adaptive $k$-NN algorithm. This is particularly evident when the number of samples in the training data is limited, suggesting that the $kK$-NN is capable of learning more discriminant functions with less data considering many relevant cases.

The 15-minute city concept, advocating for cities where essential services are accessible within 15 minutes on foot and by bike, has gained significant attention in recent years. However, despite being celebrated for promoting sustainability, there is an ongoing debate regarding its effectiveness in reducing car usage and, subsequently, emissions in cities. In particular, large-scale evaluations of the effectiveness of the 15-minute concept in reducing emissions are lacking. To address this gap, we investigate whether cities with better walking accessibility, like 15-minute cities, are associated with lower transportation emissions. Comparing 700 cities worldwide, we find that cities with better walking accessibility to services emit less CO$_2$ per capita for transport. Moreover, we observe that among cities with similar average accessibility, cities spreading over larger areas tend to emit more. Our findings highlight the effectiveness of decentralised urban planning, especially the proximity-based 15-minute city, in promoting sustainable mobility. However, they also emphasise the need to integrate local accessibility with urban compactness and efficient public transit, which are vital in large cities.

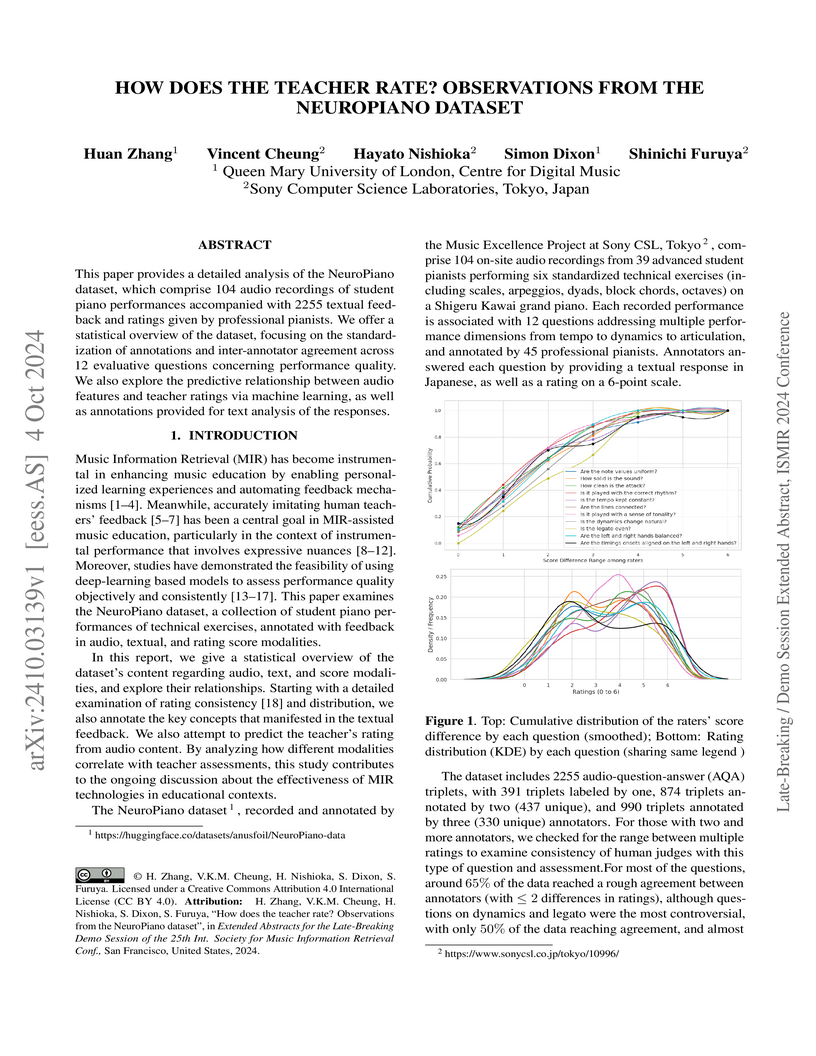
This paper provides a detailed analysis of the NeuroPiano dataset, which comprise 104 audio recordings of student piano performances accompanied with 2255 textual feedback and ratings given by professional pianists. We offer a statistical overview of the dataset, focusing on the standardization of annotations and inter-annotator agreement across 12 evaluative questions concerning performance quality. We also explore the predictive relationship between audio features and teacher ratings via machine learning, as well as annotations provided for text analysis of the responses.