Universite de Toulon
Researchers from Apple and Universit
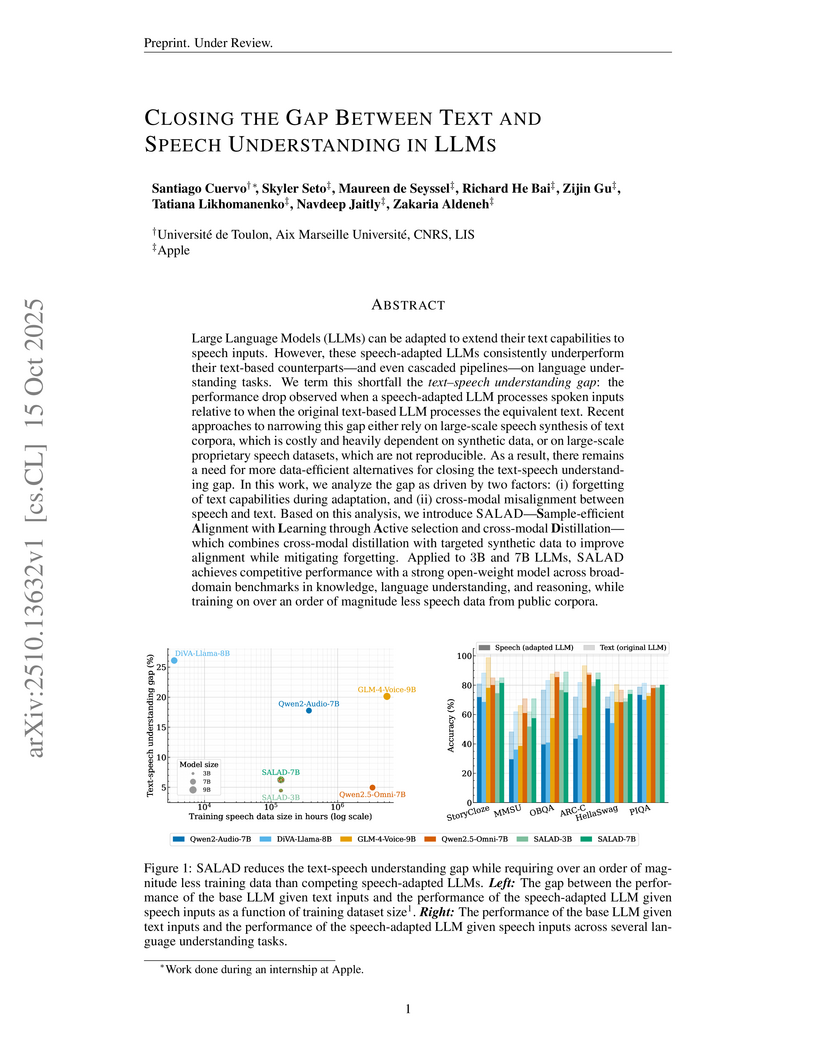
de Toulon introduced SALAD, a sample-efficient method that significantly reduces the performance gap between text and speech understanding in large language models. This approach leverages cross-modal distillation and active selection, achieving competitive results on broad-domain tasks with over an order of magnitude less public speech data than comparable models while preserving text capabilities.
I investigate spacetime singularities from the point of view of the wavefunction of the universe. In order to extend the classical notion of geodesic incompleteness one has to include the proper time of an observer as a degree of freedom in the Wheeler DeWitt equation. This leads to a Schrödinger equation along the observer worldline. Near the singularity, as in the classical BLK treatment, I ignore spatial gradients and effectively describe the spacetime around the worldline in the mini-superspace approximation. Then the problem proves identical to a spherically symmetric scattering of a quantum particle off a central potential and singularity avoidance is tantamount to unitary evolution for this system. Standard types of matter (dust, radiation) correspond to regular potentials and thus lead to a bounce. The most singular component, spatial anisotropy, is associated to a conserved charge and yields a negative inverse-square potential -- like standard angular momentum, but with opposite sign. This potential is critical, in that the unitarity of the evolution depends on the actual numerical factor in front of it, i.e., on the anisotropy charge.
31 Jan 2019
The Adapted Modular Number System (AMNS) is a sytem of representation of integers to speed up arithmetic operations modulo a prime p. Such a system can be defined by a tuple (p, n, {\gamma}, {\rho}, E) where E is in Z[X]. In [13] conditions are given to build AMNS with E(X) = {X^n +1}. In this paper, we generalize their results and show how to generate multiple AMNS for a given prime p with E(X)={X^n-\lambda} and {\lambda} in Z. Moreover, we propose a complete set of algorithms without conditional branching to perform arithmetic and conversion operations in the AMNS, using a Montgomery-like method described in [15].
We perform a detailed, fully-correlated study of the chiral behavior of the pion mass and decay constant, based on 2+1 flavor lattice QCD simulations. These calculations are implemented using tree-level, O(a)-improved Wilson fermions, at four values of the lattice spacing down to 0.054 fm and all the way down to below the physical value of the pion mass. They allow a sharp comparison with the predictions of SU(2) chiral perturbation theory (\chi PT) and a determination of some of its low energy constants. In particular, we systematically explore the range of applicability of NLO SU(2) \chi PT in two different expansions: the first in quark mass (x-expansion), and the second in pion mass (\xi-expansion). We find that these expansions begin showing signs of failure around M_\pi=300 MeV for the typical percent-level precision of our N_f=2+1 lattice results. We further determine the LO low energy constants (LECs), F=88.0 \pm 1.3\pm 0.3 and B^\msbar(2 GeV)=2.58 \pm 0.07 \pm 0.02 GeV, and the related quark condensate, \Sigma^\msbar(2 GeV)=(271\pm 4\pm 1 MeV)^3, as well as the NLO ones, l_3=2.5 \pm 0.5 \pm 0.4 and l_4=3.8 \pm 0.4 \pm 0.2, with fully controlled uncertainties. We also explore the NNLO expansions and the values of NNLO LECs. In addition, we show that the lattice results favor the presence of chiral logarithms. We further demonstrate how the absence of lattice results with pion masses below 200 MeV can lead to misleading results and conclusions. Our calculations allow a fully controlled, ab initio determination of the pion decay constant with a total 1% error, which is in excellent agreement with experiment.
10 Oct 2025
For the family of the orthogonal quantum matrix algebras we investigate the structure of their characteristic subalgebras -- special commutative subalgebras, which for the subfamily of the reflection equation algebras appear to be central. In [OP1] we described three generating sets of the characteristic subalgebras of the symplectic and orthogonal quantum matrix algebras. One of these -- the set of the elementary sums -- is finite. In the symplectic case the elementary sums are in general algebraically independent. On the contrary, in the orthogonal case the elementary sums turn out to be dependent. We obtain a set of quadratic reciprocal relations for these generators. Next, we resolve the reciprocal relations for the quantum orthogonal matrix algebra extended by the inverse of the quantum matrix. As an auxiliary result, we derive the commutation relations between the q-determinant of the quantum orthogonal matrix and the generators of the quantum matrix algebra, that is, the components of the quantum matrix.
08 May 2017
We study simple effective models of fermionic WIMP dark matter, where the dark matter candidate is a mixture of a Standard Model singlet and an n-plet of SU(2) with n >= 3, stabilized by a discrete symmetry. The dark matter mass is assumed to be around the electroweak scale, and the mixing is generated by higher-dimensional operators, with a cutoff scale > 1 TeV. For appropriate values of the mass parameters and the mixing we find that the observed dark matter relic density can be generated by coannihilation. Direct detection experiments have already excluded large parts of the parameter space, and the next-generation experiments will further constrain these models.
02 Sep 2024
We simulate Nf=2+1 QCD at the physical point combining open and periodic boundary conditions in a parallel tempering framework, following the original proposal by M. Hasenbusch for 2d CPN−1 models, which has been recently implemented and widely employed in 4d SU(N) pure Yang-Mills theories too. We show that using this algorithm it is possible to achieve a sizable reduction of the auto-correlation time of the topological charge in dynamical fermions simulations both at zero and finite temperature, allowing to avoid topology freezing down to lattice spacings as fine as a∼0.02 fm. Therefore, this implementation of the Parallel Tempering on Boundary Conditions algorithm has the potential to substantially push forward the investigation of the QCD vacuum properties by means of lattice simulations.
 CNRSUniversity of OsloSLAC National Accelerator Laboratory
CNRSUniversity of OsloSLAC National Accelerator Laboratory Chinese Academy of Sciences
Chinese Academy of Sciences UC Berkeley
UC Berkeley University College London
University College London the University of Tokyo
the University of Tokyo Stanford University
Stanford University University of MichiganUniversity of Edinburgh
University of MichiganUniversity of Edinburgh Boston UniversitySouthern Methodist UniversityUniversidad de GranadaUniversity of Innsbruck
Boston UniversitySouthern Methodist UniversityUniversidad de GranadaUniversity of Innsbruck Johns Hopkins UniversityThe University of Texas at DallasUniversity of Colorado
Johns Hopkins UniversityThe University of Texas at DallasUniversity of Colorado Lawrence Berkeley National Laboratory
Lawrence Berkeley National Laboratory CEA
CEA The Ohio State University
The Ohio State University Durham UniversitySejong UniversitySharif University of TechnologySwinburne University of TechnologyUniversidad de Los AndesThe Barcelona Institute of Science and TechnologyUniversidad Nacional de ColombiaCIEMATInstituto de Astrofísica de Andalucía, IAA-CSICInstitut de Física d’Altes Energies (IFAE)Observatoire de la Cˆote d’AzurCenter for Cosmology and AstroParticle PhysicsNSF’s National Optical-Infrared Astronomy Research LaboratorySiena CollegeOhio UniversityKavli Institute for Particle Astrophysics and CosmologyUniversite de ToulonUniversidad Nacional Autonoma de MexicoAIMUniversit\'e C\^ote d'AzurKavli Institute for the Physics and Mathematics of the Universe (WPI),Aix-Marseille Universit\'eInstitut de Ci`encies de L’Espai (IEEC-CSIC)Port d’Informaci´o Cient´ıficaUniversit´e Paris Cit´eInstituto de F́ısica Téorica UAM/CSICUniversité Paris-SaclayINAF
Osservatorio Astrofisico di ArcetriInstituciò Catalana de Recerca i Estudis AvancatsINAF
Osservatorio Astronomico di Brera
Durham UniversitySejong UniversitySharif University of TechnologySwinburne University of TechnologyUniversidad de Los AndesThe Barcelona Institute of Science and TechnologyUniversidad Nacional de ColombiaCIEMATInstituto de Astrofísica de Andalucía, IAA-CSICInstitut de Física d’Altes Energies (IFAE)Observatoire de la Cˆote d’AzurCenter for Cosmology and AstroParticle PhysicsNSF’s National Optical-Infrared Astronomy Research LaboratorySiena CollegeOhio UniversityKavli Institute for Particle Astrophysics and CosmologyUniversite de ToulonUniversidad Nacional Autonoma de MexicoAIMUniversit\'e C\^ote d'AzurKavli Institute for the Physics and Mathematics of the Universe (WPI),Aix-Marseille Universit\'eInstitut de Ci`encies de L’Espai (IEEC-CSIC)Port d’Informaci´o Cient´ıficaUniversit´e Paris Cit´eInstituto de F́ısica Téorica UAM/CSICUniversité Paris-SaclayINAF
Osservatorio Astrofisico di ArcetriInstituciò Catalana de Recerca i Estudis AvancatsINAF
Osservatorio Astronomico di BreraThe Dark Energy Spectroscopic Instrument (DESI) survey will measure spectroscopic redshifts for millions of galaxies across roughly 14,000deg2 of the sky. Cross-correlating targets in the DESI survey with complementary imaging surveys allows us to measure and analyze shear distortions caused by gravitational lensing in unprecedented detail. In this work, we analyze a series of mock catalogs with ray-traced gravitational lensing and increasing sophistication to estimate systematic effects on galaxy-galaxy lensing estimators such as the tangential shear γt and the excess surface density ΔΣ. We employ mock catalogs tailored to the specific imaging surveys overlapping with the DESI survey: the Dark Energy Survey (DES), the Hyper Suprime-Cam (HSC) survey, and the Kilo-Degree Survey (KiDS). Among others, we find that fiber incompleteness can have significant effects on galaxy-galaxy lensing estimators but can be corrected effectively by up-weighting DESI targets with fibers by the inverse of the fiber assignment probability. Similarly, we show that intrinsic alignment and lens magnification are expected to be statistically significant given the precision forecasted for the DESI year-1 data set. Our study informs several analysis choices for upcoming cross-correlation studies of DESI with DES, HSC, and KiDS.
31 Jan 2019
The Adapted Modular Number System (AMNS) is a sytem of representation of integers to speed up arithmetic operations modulo a prime p. Such a system can be defined by a tuple (p, n, {\gamma}, {\rho}, E) where E is in Z[X]. In [13] conditions are given to build AMNS with E(X) = {X^n +1}. In this paper, we generalize their results and show how to generate multiple AMNS for a given prime p with E(X)={X^n-\lambda} and {\lambda} in Z. Moreover, we propose a complete set of algorithms without conditional branching to perform arithmetic and conversion operations in the AMNS, using a Montgomery-like method described in [15].
We present a detailed analysis of the kinetic and mass terms associated with the Landau gauge gluon propagator in the presence of dynamical quarks, and a comprehensive dynamical study of certain special kinematic limits of the three-gluon vertex. Our approach capitalizes on results from recent lattice simulations with (2+1) domain wall fermions, a novel nonlinear treatment of the gluon mass equation, and the nonperturbative reconstruction of the longitudinal three-gluon vertex from its fundamental Slavnov-Taylor identities. Particular emphasis is placed on the persistence of the suppression displayed by certain combinations of the vertex form factors at intermediate and low momenta, already known from numerous pure Yang-Mills studies. One of our central findings is that the inclusion of dynamical quarks moderates the intensity of this phenomenon only mildly, leaving the asymptotic low-momentum behavior unaltered, but displaces the characteristic "zero crossing" deeper into the infrared region. In addition, the effect of the three-gluon vertex is explored at the level of the renormalization-group invariant combination corresponding to the effective gauge coupling, whose size is considerably reduced with respect to its counterpart obtained from the ghost-gluon vertex. The main upshot of the above considerations is the further confirmation of the tightly interwoven dynamics between the two- and three-point sectors of QCD.
The well-known 5-parameter isometry group of plane gravitational waves in 4 dimensions is identified as Levy-Leblond's Carroll group in 2+1 dimensions with no rotations. Our clue is that plane waves are Bargmann spaces into which Carroll manifolds can be embedded. We also comment on the scattering of light by a gravitational wave and calculate its electric permittivity considered as an impedance-matched metamaterial.
03 May 2016
 CNRSNikhef
CNRSNikhef INFNUniversità di GenovaUniversiteit LeidenObservatoire de ParisIRDUniversitat Polit`ecnica de Val`enciaErlangen Centre for Astroparticle PhysicsObservatoire de la Cˆote d’AzurUniv. Paris-SudUniversiteit van AmsterdamLAM (Laboratoire d’Astrophysique de Marseille)Universite de ToulonTechnical University of CataloniaINFN Laboratori Nazionali del SudUniversit\'e C\^ote d'AzurCEA/IrfuUniversity Mohammed IAPCSorbonne Paris CiteUniversit´e Paris DiderotLaboratoire de Physique CorpusculaireGeoazurAix-Marseille Universit\'eUniversitat WurzburgRoyal Netherlands Institute for Sea Research (NIOZ)LSISInstitute for Space ScienceUniversite Blaise PascalUniversite de Haute AlsaceDr. Remeis SternwarteClermont UniversiteIFIC (Instituto de F´ısica Corpuscular)GRPHEInstitut d’Investigaci´o per a la Gesti´o Integrada de les Zones Costaneres (IGIC)Universita’ ”La Sapienza”Friedrich-Alexander Universität, Erlangen-NürnbergUniversit
Di Bologna
INFNUniversità di GenovaUniversiteit LeidenObservatoire de ParisIRDUniversitat Polit`ecnica de Val`enciaErlangen Centre for Astroparticle PhysicsObservatoire de la Cˆote d’AzurUniv. Paris-SudUniversiteit van AmsterdamLAM (Laboratoire d’Astrophysique de Marseille)Universite de ToulonTechnical University of CataloniaINFN Laboratori Nazionali del SudUniversit\'e C\^ote d'AzurCEA/IrfuUniversity Mohammed IAPCSorbonne Paris CiteUniversit´e Paris DiderotLaboratoire de Physique CorpusculaireGeoazurAix-Marseille Universit\'eUniversitat WurzburgRoyal Netherlands Institute for Sea Research (NIOZ)LSISInstitute for Space ScienceUniversite Blaise PascalUniversite de Haute AlsaceDr. Remeis SternwarteClermont UniversiteIFIC (Instituto de F´ısica Corpuscular)GRPHEInstitut d’Investigaci´o per a la Gesti´o Integrada de les Zones Costaneres (IGIC)Universita’ ”La Sapienza”Friedrich-Alexander Universität, Erlangen-NürnbergUniversit
Di BolognaA search for Secluded Dark Matter annihilation in the Sun using 2007-2012 data of the ANTARES neutrino telescope is presented. Three different cases are considered: a) detection of dimuons that result from the decay of the mediator, or neutrino detection from: b) mediator that decays into a dimuon and, in turn, into neutrinos, and c) mediator that decays directly into neutrinos. As no significant excess over background is observed, constraints are derived on the dark matter mass and the lifetime of the mediator.
We study the exact square chromatic number of subcubic planar graphs. An exact square coloring of a graph G is a vertex-coloring in which any two vertices at distance exactly 2 receive distinct colors. The smallest number of colors used in such a coloring of G is its exact square chromatic number, denoted χ♯2(G). This notion is related to other types of distance-based colorings, as well as to injective coloring. Indeed, for triangle-free graphs, exact square coloring and injective coloring coincide. We prove tight bounds on special subclasses of planar graphs: subcubic bipartite planar graphs and subcubic K 4-minor-free graphs have exact square chromatic number at most 4. We then turn our attention to the class of fullerene graphs, which are cubic planar graphs with face sizes 5 and 6. We characterize fullerene graphs with exact square chromatic number 3. Furthermore, supporting a conjecture of Chen, Hahn, Raspaud and Wang (that all subcubic planar graphs are injectively 5-colorable) we prove that any induced subgraph of a fullerene graph has exact square chromatic number at most 5. This is done by first proving that a minimum counterexample has to be on at most 80 vertices and then computationally verifying the claim for all such graphs.
The MacWilliams Extension Theorem states that each linear Hamming isometry of a linear code extends to a monomial map. In this paper an analogue of the extension theorem for linear codes over a module alphabet is observed. A geometric approach to the extendability of isometries is described. For a matrix module alphabet we found the minimum length of a code for which an unextendable Hamming isometry exists. We also proved an extension theorem for MDS codes over a module alphabet.
14 Sep 2025
We develop an inductive approach to obtaining stochastic estimates for the φ24-equation when the coefficient field is correlated with the driving noise. Our method is based on (infinite-dimensional) Gaussian integration by parts with respect to Wick products of Gaussian random variables (more precisely, mollifications of space-time white noise)
Quantum tunneling of a black hole into a white hole provides a model for the full life cycle of a black hole. The white hole acts as a long-lived remnant, solving the black-hole information paradox. The remnant solution of the paradox has long been viewed with suspicion, mostly because remnants seemed to be such exotic objects. We point out that (i) established physics includes objects with precisely the required properties for remnants: white holes with small masses but large finite interiors; (ii) non-perturbative quantum-gravity indicates that a black hole tunnels precisely into such a white hole, at the end of its evaporation. We address the objections to the existence of white-hole remnants, discuss their stability, and show how the notions of entropy relevant in this context allow them to evade several no-go arguments. A black hole's formation, evaporation, tunneling to a white hole, and final slow decay, form a unitary process that does not violate any known physics.
19 Aug 2025
Consider a reference homogeneous and isotropic electromagnetic waveguide with a simply connected cross-section embedded in a perfect conductor. In this setting, when the waveguide is straight, the spectrum of the associated self-adjoint Maxwell operator with a constant twist (which may be zero) lies on the real line and is symmetric with respect to zero and exhibits a spectral gap around the origin. Moreover, the spectrum is purely essential, and contains 0 which is an eigenvalue of infinite multiplicity. In this work, we present new results on the effects of geometric deformations, specifically bending and twisting, on the spectrum of the Maxwell operator. More precisely, we provide, on the one hand, sufficient conditions on the asymptotic behavior of curvature and twist that ensure the preservation of the essential spectrum of the reference waveguide. Our approach relies on a Birman-Schwinger-type principle, which may be of independent interest and applicable in other contexts. On the other hand, we give sufficient conditions (involving in particular the geometrical shape of the cross-section of the waveguide) so that the geometrical deformation creates discrete spectrum (namely isolated eigenvalues of finite multiplicity) within the gap of the essential spectrum. In addition, we give some results on the localization of these discrete eigenvalues. The sufficient condition involving the cross-section is then studied both analytically and numerically. Finally, we examine its stability under shape deformations of the cross-section, focusing in particular on the case of a waveguide with a rectangular cross-section.
02 Jun 2025
Quantum transport anomalies in systems obeying Haldane-Wu fractional exclusion statistics, characterized by the statistical interactions parameter g are investigated. We identify particle-hole symmetry breaking of the Haldane-Wu distribution function via its deviations of the maximum entropy (Sgmax), evaluated at the chemical potential, from the value kBln2 (a value that holds only at the free fermion limit, g=1). A duality relation, gSgmax=S1/gmax, quantifying the degree of violation is obtained. This symmetry breaking manifests in transport phenomena as: significant violations of the Wiedemann-Franz law arising for g>1 (but remain absent for g≤1) across a broad temperature range. Moreover, the thermoelectric figure of merit ZT is substantially enhanced for g>1 and suppressed for g<1, indicating new routes to optimize energy conversion. These results deepen the understanding of the interplay between equilibrium statistics and transport, suggesting avenues for engineering advanced thermoelectric materials.
Vertex amplitudes are elementary contributions to the transition amplitudes in the spin foam models of quantum gravity. The purpose of this article is make the first step towards computing vertex amplitudes with the use of quantum algorithms. In our studies we are focused on a vertex amplitude of 3+1 D gravity, associated with a pentagram spin-network. Furthermore, all spin labels of the spin network are assumed to be equal j=1/2, which is crucial for the introduction of the \emph{intertwiner qubits}. A procedure of determining modulus squares of vertex amplitudes on universal quantum computers is proposed. Utility of the approach is tested with the use of: IBM's \emph{ibmqx4} 5-qubit quantum computer, simulator of quantum computer provided by the same company and QX quantum computer simulator. Finally, values of the vertex probability are determined employing both the QX and the IBM simulators with 20-qubit quantum register and compared with analytical predictions.
We perform a lattice QCD calculation of the hadronic light-by-light contribution to (g−2)μ at the SU(3) flavor-symmetric point mπ=mK≃420MeV. The representation used is based on coordinate-space perturbation theory, with all QED elements of the relevant Feynman diagrams implemented in continuum, infinite Euclidean space. As a consequence, the effect of using finite lattices to evaluate the QCD four-point function of the electromagnetic current is exponentially suppressed. Thanks to the SU(3)-flavor symmetry, only two topologies of diagrams contribute, the fully connected and the leading disconnected. We show the equivalence in the continuum limit of two methods of computing the connected contribution, and introduce a sparse-grid technique for computing the disconnected contribution. Thanks to our previous calculation of the pion transition form factor, we are able to correct for the residual finite-size effects and extend the tail of the integrand. We test our understanding of finite-size effects by using gauge ensembles differing only by their volume. After a continuum extrapolation based on four lattice spacings, we obtain aμhlbl=(65.4±4.9±6.6)×10−11, where the first error results from the uncertainties on the individual gauge ensembles and the second is the systematic error of the continuum extrapolation. Finally, we estimate how this value will change as the light-quark masses are lowered to their physical values.
There are no more papers matching your filters at the moment.