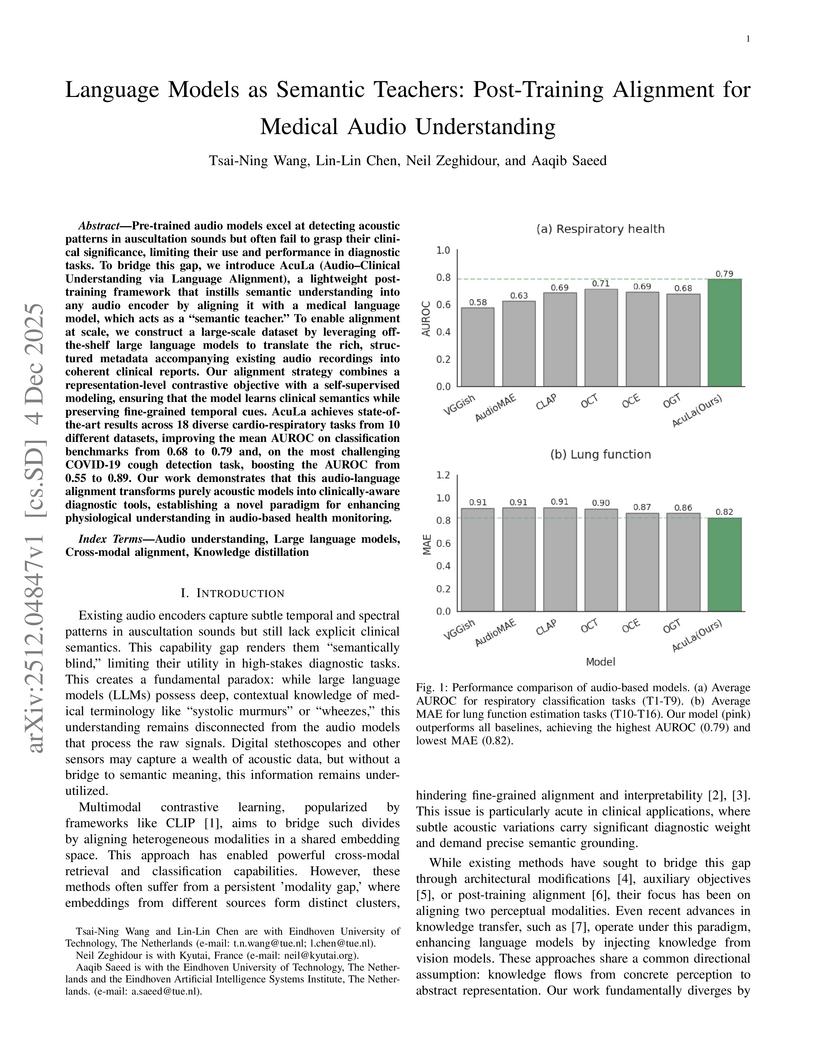
Pre-trained audio models excel at detecting acoustic patterns in auscultation sounds but often fail to grasp their clinical significance, limiting their use and performance in diagnostic tasks. To bridge this gap, we introduce AcuLa (Audio-Clinical Understanding via Language Alignment), a lightweight post-training framework that instills semantic understanding into any audio encoder by aligning it with a medical language model, which acts as a "semantic teacher." To enable alignment at scale, we construct a large-scale dataset by leveraging off-the-shelf large language models to translate the rich, structured metadata accompanying existing audio recordings into coherent clinical reports. Our alignment strategy combines a representation-level contrastive objective with a self-supervised modeling, ensuring that the model learns clinical semantics while preserving fine-grained temporal cues. AcuLa achieves state-of-the-art results across 18 diverse cardio-respiratory tasks from 10 different datasets, improving the mean AUROC on classification benchmarks from 0.68 to 0.79 and, on the most challenging COVID-19 cough detection task, boosting the AUROC from 0.55 to 0.89. Our work demonstrates that this audio-language alignment transforms purely acoustic models into clinically-aware diagnostic tools, establishing a novel paradigm for enhancing physiological understanding in audio-based health monitoring.

Automating the current bridge visual inspection practices using drones and image processing techniques is a prominent way to make these inspections more effective, robust, and less expensive. In this paper, we investigate the development of a novel deep-learning method for the detection of fatigue cracks in high-resolution images of steel bridges. First, we present a novel and challenging dataset comprising of images of cracks in steel bridges. Secondly, we integrate the ConvNext neural network with a previous state-of-the-art encoder-decoder network for crack segmentation. We study and report, the effects of the use of background patches on the network performance when applied to high-resolution images of cracks in steel bridges. Finally, we introduce a loss function that allows the use of more background patches for the training process, which yields a significant reduction in false positive rates.

Evaluating feature attribution methods represents a critical challenge in explainable AI (XAI), as researchers typically rely on perturbation-based metrics when ground truth is unavailable. However, recent work demonstrates that these evaluation metrics can show different performance across predicted classes within the same dataset. These "class-dependent evaluation effects" raise questions about whether perturbation analysis reliably measures attribution quality, with direct implications for XAI method development and the trustworthiness of evaluation techniques. We investigate under which conditions these class-dependent effects arise by conducting controlled experiments with synthetic time series data where ground truth feature locations are known. We systematically vary feature types and class contrasts across binary classification tasks, then compare perturbation-based degradation scores with ground truth-based precision-recall metrics using multiple attribution methods. Our experiments demonstrate that class-dependent effects emerge with both evaluation approaches even in simple scenarios with temporally localized features, triggered by basic variations in feature amplitude or temporal extent between classes. Most critically, we find that perturbation-based and ground truth metrics frequently yield contradictory assessments of attribution quality across classes, with weak correlations between evaluation approaches. These findings suggest that researchers should interpret perturbation-based metrics with care, as they may not always align with whether attributions correctly identify discriminating features. These findings reveal opportunities to reconsider what attribution evaluation actually measures and to develop more comprehensive evaluation frameworks that capture multiple dimensions of attribution quality.

Understanding the dynamics of pedestrian crowds is an outstanding challenge crucial for designing efficient urban infrastructure and ensuring safe crowd management. To this end, both small-scale laboratory and large-scale real-world measurements have been used. However, these approaches respectively lack statistical resolution and parametric controllability, both essential to discovering physical relationships underlying the complex stochastic dynamics of crowds. Here, we establish an investigation paradigm that offers laboratory-like controllability, while ensuring the statistical resolution of large-scale real-world datasets. Using our data-driven Neural Crowd Simulator (NeCS), which we train on large-scale data and validate against key statistical features of crowd dynamics, we show that we can perform effective surrogate crowd dynamics experiments without training on specific scenarios. We not only reproduce known experimental results on pairwise avoidance, but also uncover the vision-guided and topological nature of N-body interactions. These findings show how virtual experiments based on neural simulation enable data-driven scientific discovery.

In this paper, we demonstrate that controllers designed by artificial potential fields (APFs) can be derived from reciprocal control barrier function quadratic program (RCBF-QP) safety filters. By integrating APFs within the RCBF-QP framework, we explicitly establish the relationship between these two approaches. Specifically, we first introduce the concepts of tightened control Lyapunov functions (T-CLFs) and tightened reciprocal control barrier functions (T-RCBFs), each of which incorporates a flexible auxiliary function. We then utilize an attractive potential field as a T-CLF to guide the nominal controller design, and a repulsive potential field as a T-RCBF to formulate an RCBF-QP safety filter. With appropriately chosen auxiliary functions, we show that controllers designed by APFs and those derived by RCBF-QP safety filters are equivalent. Based on this insight, we further generalize the APF-based controllers (equivalently, RCBF-QP safety filter-based controllers) to more general scenarios without restricting the choice of auxiliary functions. Finally, we present a collision avoidance example to clearly illustrate the connection and equivalence between the two methods.

Dynamic task assignment involves assigning arriving tasks to a limited number of resources in order to minimize the overall cost of the assignments. To achieve optimal task assignment, it is necessary to model the assignment problem first. While there exist separate formalisms, specifically Markov Decision Processes and (Colored) Petri Nets, to model, execute, and solve different aspects of the problem, there is no integrated modeling technique. To address this gap, this paper proposes Action-Evolution Petri Nets (A-E PN) as a framework for modeling and solving dynamic task assignment problems. A-E PN provides a unified modeling technique that can represent all elements of dynamic task assignment problems. Moreover, A-E PN models are executable, which means they can be used to learn close-to-optimal assignment policies through Reinforcement Learning (RL) without additional modeling effort. To evaluate the framework, we define a taxonomy of archetypical assignment problems. We show for three cases that A-E PN can be used to learn close-to-optimal assignment policies. Our results suggest that A-E PN can be used to model and solve a broad range of dynamic task assignment problems.

The Dynamic Task Assignment Problem (DTAP) concerns matching resources to tasks in real time while minimizing some objectives, like resource costs or task cycle time. In this work, we consider a DTAP variant where every task is a case composed of a stochastic sequence of activities. The DTAP, in this case, involves the decision of which employee to assign to which activity to process requests as quickly as possible. In recent years, Deep Reinforcement Learning (DRL) has emerged as a promising tool for tackling this DTAP variant, but most research is limited to solving small-scale, synthetic problems, neglecting the challenges posed by real-world use cases. To bridge this gap, this work proposes a DRL-based Decision Support System (DSS) for real-world scale DTAPS. To this end, we introduce a DRL agent with two novel elements: a graph structure for observations and actions that can effectively represent any DTAP and a reward function that is provably equivalent to the objective of minimizing the average cycle time of tasks. The combination of these two novelties allows the agent to learn effective and generalizable assignment policies for real-world scale DTAPs. The proposed DSS is evaluated on five DTAP instances whose parameters are extracted from real-world logs through process mining. The experimental evaluation shows how the proposed DRL agent matches or outperforms the best baseline in all DTAP instances and generalizes on different time horizons and across instances.

Sontag's universal formula is a widely used technique for stabilizing control through control Lyapunov functions. Recently, it has been extended to address safety-critical control by incorporating control barrier functions (CBFs). However, deriving a universal formula that satisfies requirements on essential properties, including safety, smoothness, and robustness against input disturbances, is still an open problem. To address this challenge, this paper introduces a novel solution - a tunable universal formula - by incorporating a (state-dependent) tunable term into Sontag's formula. This tunable term enables the regulation of safety-critical control performances, allowing the attainment of desired properties through a proper selection of tunable terms. Generally, the tunable universal formula can be seen as a controller that improves the quadratic program (QP)-synthesized controllers in terms of robustness and smoothness, while also reducing the conservatism (corresponding to robustness) in Sontag's formula. Furthermore, we extend the tunable universal formula to address safety-critical control problems with norm-bounded input constraints, showcasing its applicability across diverse control scenarios. Finally, we demonstrate the efficacy of our method through a two-link manipulator safe tracking example, investigating the essential properties including safety, smoothness, and robustness against input disturbances under various tunable terms.

Dynamic task assignment concerns the optimal assignment of resources to tasks in a business process. Recently, Deep Reinforcement Learning (DRL) has been proposed as the state of the art for solving assignment problems. DRL methods usually employ a neural network (NN) as an approximator for the policy function, which ingests the state of the process and outputs a valuation of the possible assignments. However, representing the state and the possible assignments so that they can serve as inputs and outputs for a policy NN remains an open challenge, especially when tasks or resources have features with an infinite number of possible values. To solve this problem, this paper proposes a method for representing and solving assignment problems with infinite state and action spaces. In doing so, it provides three contributions: (I) A graph-based feature representation of assignment problems, which we call assignment graph; (II) A mapping from marked Colored Petri Nets to assignment graphs; (III) An adaptation of the Proximal Policy Optimization algorithm that can learn to solve assignment problems represented through assignment graphs. To evaluate the proposed representation method, we model three archetypal assignment problems ranging from finite to infinite state and action space dimensionalities. The experiments show that the method is suitable for representing and learning close-to-optimal task assignment policies regardless of the state and action space dimensionalities.

Distal myopathy represents a genetically heterogeneous group of skeletal muscle disorders with broad clinical manifestations, posing diagnostic challenges in radiology. To address this, we propose a novel multimodal attention-aware fusion architecture that combines features extracted from two distinct deep learning models, one capturing global contextual information and the other focusing on local details, representing complementary aspects of the input data. Uniquely, our approach integrates these features through an attention gate mechanism, enhancing both predictive performance and interpretability. Our method achieves a high classification accuracy on the BUSI benchmark and a proprietary distal myopathy dataset, while also generating clinically relevant saliency maps that support transparent decision-making in medical diagnosis. We rigorously evaluated interpretability through (1) functionally grounded metrics, coherence scoring against reference masks and incremental deletion analysis, and (2) application-grounded validation with seven expert radiologists. While our fusion strategy boosts predictive performance relative to single-stream and alternative fusion strategies, both quantitative and qualitative evaluations reveal persistent gaps in anatomical specificity and clinical usefulness of the interpretability. These findings highlight the need for richer, context-aware interpretability methods and human-in-the-loop feedback to meet clinicians' expectations in real-world diagnostic settings.

Distal myopathy represents a genetically heterogeneous group of skeletal muscle disorders with broad clinical manifestations, posing diagnostic challenges in radiology. To address this, we propose a novel multimodal attention-aware fusion architecture that combines features extracted from two distinct deep learning models, one capturing global contextual information and the other focusing on local details, representing complementary aspects of the input data. Uniquely, our approach integrates these features through an attention gate mechanism, enhancing both predictive performance and interpretability. Our method achieves a high classification accuracy on the BUSI benchmark and a proprietary distal myopathy dataset, while also generating clinically relevant saliency maps that support transparent decision-making in medical diagnosis. We rigorously evaluated interpretability through (1) functionally grounded metrics, coherence scoring against reference masks and incremental deletion analysis, and (2) application-grounded validation with seven expert radiologists. While our fusion strategy boosts predictive performance relative to single-stream and alternative fusion strategies, both quantitative and qualitative evaluations reveal persistent gaps in anatomical specificity and clinical usefulness of the interpretability. These findings highlight the need for richer, context-aware interpretability methods and human-in-the-loop feedback to meet clinicians' expectations in real-world diagnostic settings.

We consider the problem of estimating a temperature-dependent thermal conductivity model (curve) from temperature measurements. We apply a Bayesian estimation approach that takes into account measurement errors and limited prior information of system properties. The approach intertwines system simulation and Markov chain Monte Carlo (MCMC) sampling. We investigate the impact of assuming different model classes - cubic polynomials and piecewise linear functions - their parametrization, and different types of prior information - ranging from uninformative to informative. Piecewise linear functions require more parameters (conductivity values) to be estimated than the four parameters (coefficients or conductivity values) needed for cubic polynomials. The former model class is more flexible, but the latter requires less MCMC samples. While parametrizing polynomials with coefficients may feel more natural, it turns out that parametrizing them using conductivity values is far more natural for the specification of prior information. Robust estimation is possible for all model classes and parametrizations, as long as the prior information is accurate or not too informative. Gaussian Markov random field priors are especially well-suited for piecewise linear functions.

Safe stabilization is a significant challenge for quadrotors, which involves reaching a goal position while avoiding obstacles. Most of the existing solutions for this problem rely on optimization-based methods, demanding substantial onboard computational resources. This paper introduces a novel approach to address this issue and provides a solution that offers fast computational capabilities tailored for onboard execution. Drawing inspiration from Sontag's universal formula, we propose an analytical control strategy that incorporates the conditions of control Lyapunov functions (CLFs) and control barrier functions (CBFs), effectively avoiding the need for solving optimization problems onboard. Moreover, we extend our approach by incorporating the concepts of input-to-state stability (ISS) and input-to-state safety (ISSf), enhancing the universal formula's capacity to effectively manage disturbances. Furthermore, we present a projection-based approach to ensure that the universal formula remains effective even when faced with control input constraints. The basic idea of this approach is to project the control input derived from the universal formula onto the closest point within the control input domain. Through comprehensive simulations and experimental results, we validate the efficacy and highlight the advantages of our methodology.