Toyota Technological Institute
The four-dimensional Chern-Simons (CS) theory provides a systematic procedure for realizing two-dimensional integrable field theories. It is therefore a natural question to ask whether integrable deformations of the theories can be realized in the four-dimensional CS theory. In this work, we study TTˉ and root-TTˉ deformations of two-dimensional integrable field theories, formulated in terms of dynamical coordinate transformations, within the framework of four-dimensional CS theory coupled to disorder defects. We illustrate our procedure in detail for the degenerate E-model, a specific construction that captures and unifies a broad range of integrable systems, including the principal chiral model.
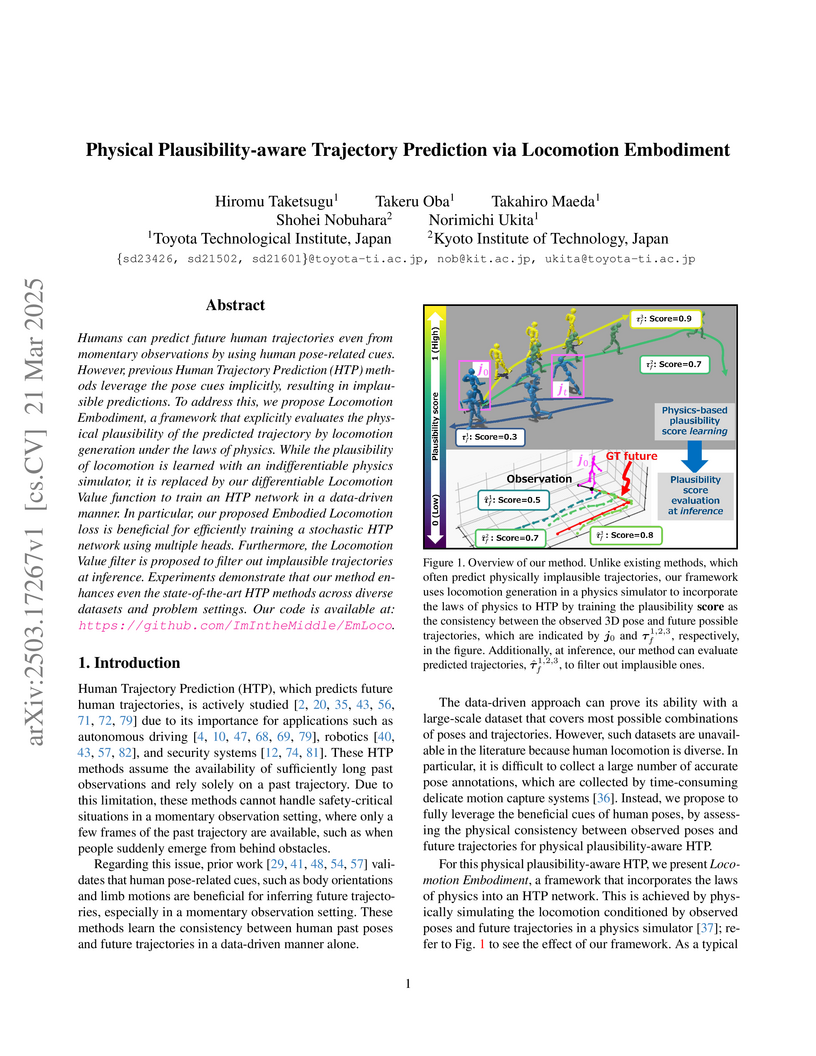
This paper presents a Locomotion Embodiment framework that integrates physics-based constraints into human trajectory prediction, addressing the challenge of generating physically plausible movements from limited observation data. The framework introduces a differentiable LocoVal function to approximate physical plausibility and an EmLoco loss for training, resulting in predictions with enhanced physical realism and improved accuracy (lower ADE/FDE) on JTA and JRDB datasets compared to existing methods.
This paper proposes Group Activity Feature (GAF) learning in which features of multi-person activity are learned as a compact latent vector. Unlike prior work in which the manual annotation of group activities is required for supervised learning, our method learns the GAF through person attribute prediction without group activity annotations. By learning the whole network in an end-to-end manner so that the GAF is required for predicting the person attributes of people in a group, the GAF is trained as the features of multi-person activity. As a person attribute, we propose to use a person's action class and appearance features because the former is easy to annotate due to its simpleness, and the latter requires no manual annotation. In addition, we introduce a location-guided attribute prediction to disentangle the complex GAF for extracting the features of each target person properly. Various experimental results validate that our method outperforms SOTA methods quantitatively and qualitatively on two public datasets. Visualization of our GAF also demonstrates that our method learns the GAF representing fined-grained group activity classes. Code: this https URL.
We investigate the solution-generating technique based on the Breitenlohner-Maison (BM) linear system, for asymptotically flat, stationary, bi-axisymmetric black hole solutions with various horizon topologies in five-dimensional vacuum Einstein theory. We construct the monodromy matrix associated with the BM linear system, which provides a unified framework for describing three distinct asymptotically flat, vacuum black hole solutions with a single angular momentum in five dimensions, each with a different horizon topology: (i) the singly rotating Myers-Perry black hole, (ii) the Emparan-Reall black ring, and (iii) the Chen-Teo rotating black lens. Conversely, by solving the corresponding Riemann-Hilbert problem using the procedure developed by Katsimpouri et al., we demonstrate that factorization of the monodromy matrix exactly reproduces these vacuum solutions, thereby reconstructing the three geometries. These constitute the first explicit examples in which the factorization procedure has been carried out for black holes with non-spherical horizon topologies. In addition, we discuss how the asymptotic behavior of five-dimensional vacuum solutions at spatial infinity is reflected in the asymptotic structure of the monodromy matrix in the spectral parameter space.
 University of Science and Technology of ChinaNational Taiwan University
University of Science and Technology of ChinaNational Taiwan University Nanjing UniversityNational Cheng Kung UniversityNational Tsing-Hua UniversityToyota Motor CorporationToyota Technological InstituteAxelspace CorporationNational Institute of Technology, Oita collegeIwate Prefecture Coastal Regional Development BureauNational Yang Ming-Chiao Tung University
Nanjing UniversityNational Cheng Kung UniversityNational Tsing-Hua UniversityToyota Motor CorporationToyota Technological InstituteAxelspace CorporationNational Institute of Technology, Oita collegeIwate Prefecture Coastal Regional Development BureauNational Yang Ming-Chiao Tung UniversitySmall Multi-Object Tracking (SMOT) is particularly challenging when targets occupy only a few dozen pixels, rendering detection and appearance-based association unreliable. Building on the success of the MVA2023 SOD4SB challenge, this paper introduces the SMOT4SB challenge, which leverages temporal information to address limitations of single-frame detection. Our three main contributions are: (1) the SMOT4SB dataset, consisting of 211 UAV video sequences with 108,192 annotated frames under diverse real-world conditions, designed to capture motion entanglement where both camera and targets move freely in 3D; (2) SO-HOTA, a novel metric combining Dot Distance with HOTA to mitigate the sensitivity of IoU-based metrics to small displacements; and (3) a competitive MVA2025 challenge with 78 participants and 308 submissions, where the winning method achieved a 5.1x improvement over the baseline. This work lays a foundation for advancing SMOT in UAV scenarios with applications in bird strike avoidance, agriculture, fisheries, and ecological monitoring.
While burst Low-Resolution (LR) images are useful for improving their Super Resolution (SR) image compared to a single LR image, prior burst SR methods are trained in a deterministic manner, which produces a blurry SR image. Since such blurry images are perceptually degraded, we aim to reconstruct sharp and high-fidelity SR images by a diffusion model. Our method improves the efficiency of the diffusion model with a stochastic sampler with a high-order ODE as well as one-step diffusion using knowledge distillation. Our experimental results demonstrate that our method can reduce the runtime to 1.6 % of its baseline while maintaining the SR quality measured based on image distortion and perceptual quality.
Safety-critical applications such as autonomous vehicles and social robots require fast computation and accurate probability density estimation on trajectory prediction. To address both requirements, this paper presents a new normalizing flow-based trajectory prediction model named FlowChain. FlowChain is a stack of conditional continuously-indexed flows (CIFs) that are expressive and allow analytical probability density computation. This analytical computation is faster than the generative models that need additional approximations such as kernel density estimation. Moreover, FlowChain is more accurate than the Gaussian mixture-based models due to fewer assumptions on the estimated density. FlowChain also allows a rapid update of estimated probability densities. This update is achieved by adopting the \textit{newest observed position} and reusing the flow transformations and its log-det-jacobians that represent the \textit{motion trend}. This update is completed in less than one millisecond because this reuse greatly omits the computational cost. Experimental results showed our FlowChain achieved state-of-the-art trajectory prediction accuracy compared to previous methods. Furthermore, our FlowChain demonstrated superiority in the accuracy and speed of density estimation. Our code is available at \url{this https URL}
We construct an exact solution in four-dimensional Einstein-Maxwell-dilaton theory, describing multi-centered rotating black holes carrying both electric and magnetic charges, obtained via dimensional reduction from five-dimensional Einstein gravity. This generalizes the Majumdar-Papapetrou solution to the rotating case, and extends the recent multi-centered rotating black hole solutions of Teo and Wan to configurations with unequal electric and magnetic charges. The resulting spacetimes are free of curvature singularities, conical defects, Dirac-Misner strings, and closed timelike curves, both on and outside the horizons, provided that the black holes have either aligned or anti-aligned spin orientations.
24 Sep 2015
We show that any depth-d circuit for determining whether an n-node graph
has an s-to-t path of length at most k must have size
nΩ(k1/d/d). The previous best circuit size lower bounds for this
problem were nkexp(−O(d)) (due to Beame, Impagliazzo, and Pitassi
[BIP98]) and nΩ((logk)/d) (following from a recent formula size
lower bound of Rossman [Ros14]). Our lower bound is quite close to optimal,
since a simple construction gives depth-d circuits of size nO(k2/d)
for this problem (and strengthening our bound even to nkΩ(1/d)
would require proving that undirected connectivity is not in NC1.)
Our proof is by reduction to a new lower bound on the size of small-depth
circuits computing a skewed variant of the "Sipser functions" that have played
an important role in classical circuit lower bounds [Sip83, Yao85, H{\aa}s86].
A key ingredient in our proof of the required lower bound for these Sipser-like
functions is the use of \emph{random projections}, an extension of random
restrictions which were recently employed in [RST15]. Random projections allow
us to obtain sharper quantitative bounds while employing simpler arguments,
both conceptually and technically, than in the previous works [Ajt89, BPU92,
BIP98, Ros14].
This paper addresses a new virtual try-on problem of fitting any size of clothes to a reference person in the image domain. While previous image-based virtual try-on methods can produce highly natural try-on images, these methods fit the clothes on the person without considering the relative relationship between the physical sizes of the clothes and the person. Different from these methods, our method achieves size-variable virtual try-on in which the image size of the try-on clothes is changed depending on this relative relationship of the physical sizes. To relieve the difficulty in maintaining the physical size of the closes while synthesizing the high-fidelity image of the whole clothes, our proposed method focuses on the residual between the silhouettes of the clothes in the reference and try-on images. We also develop a size-variable virtual try-on dataset consisting of 1,524 images provided by 26 subjects. Furthermore, we propose an evaluation metric for size-variable virtual-try-on. Quantitative and qualitative experimental results show that our method can achieve size-variable virtual try-on better than general virtual try-on methods.
28 Apr 2025
This paper proposes an image-based robot motion planning method using a
one-step diffusion model. While the diffusion model allows for high-quality
motion generation, its computational cost is too expensive to control a robot
in real time. To achieve high quality and efficiency simultaneously, our
one-step diffusion model takes an approximately generated motion, which is
predicted directly from input images. This approximate motion is optimized by
additive noise provided by our novel noise optimizer. Unlike general isotropic
noise, our noise optimizer adjusts noise anisotropically depending on the
uncertainty of each motion element. Our experimental results demonstrate that
our method outperforms state-of-the-art methods while maintaining its
efficiency by one-step diffusion.
This paper proposes a novel metric for Human Motion Prediction (HMP). Since a single past sequence can lead to multiple possible futures, a probabilistic HMP method predicts such multiple motions. While a single motion predicted by a deterministic method is evaluated only with the difference from its ground truth motion, multiple predicted motions should also be evaluated based on their distribution. For this evaluation, this paper focuses on the following two criteria. \textbf{(a) Coverage}: motions should be distributed among multiple motion modes to cover diverse possibilities. \textbf{(b) Validity}: motions should be kinematically valid as future motions observable from a given past motion. However, existing metrics simply appreciate widely distributed motions even if these motions are observed in a single mode and kinematically invalid. To resolve these disadvantages, this paper proposes a Multimodality-aware Metric using Clustering-based Modes (MMCM). For (a) coverage, MMCM divides a motion space into several clusters, each of which is regarded as a mode. These modes are used to explicitly evaluate whether predicted motions are distributed among multiple modes. For (b) validity, MMCM identifies valid modes by collecting possible future motions from a motion dataset. Our experiments validate that our clustering yields sensible mode definitions and that MMCM accurately scores multimodal predictions. Code: this https URL
Image-based motion prediction is one of the essential techniques for robot
manipulation. Among the various prediction models, we focus on diffusion models
because they have achieved state-of-the-art performance in various
applications. In image-based motion prediction, diffusion models stochastically
predict contextually appropriate motion by gradually denoising random Gaussian
noise based on the image context. While diffusion models are able to predict
various motions by changing the random noise, they sometimes fail to predict a
contextually appropriate motion based on the image because the random noise is
sampled independently of the image context. To solve this problem, we propose
R2-Diff. In R2-Diff, a motion retrieved from a dataset based on image
similarity is fed into a diffusion model instead of random noise. Then, the
retrieved motion is refined through the denoising process of the diffusion
model. Since the retrieved motion is almost appropriate to the context, it
becomes easier to predict contextually appropriate motion. However, traditional
diffusion models are not optimized to refine the retrieved motion. Therefore,
we propose the method of tuning the hyperparameters based on the distance of
the nearest neighbor motion among the dataset to optimize the diffusion model
for refinement. Furthermore, we propose an image-based retrieval method to
retrieve the nearest neighbor motion in inference. Our proposed retrieval
efficiently computes the similarity based on the image features along the
motion trajectory. We demonstrate that R2-Diff accurately predicts appropriate
motions and achieves high task success rates compared to recent
state-of-the-art models in robot manipulation.
02 Jan 2022
The replica wormholes are a key to the existence of the islands that play a central role in a recent proposal for the resolution of the black hole information paradox. In this paper, we study the replica wormholes in the JT gravity, a model of two-dimensional quantum gravity coupled to a non-dynamical dilaton, by making use of the 2d conformal field theory (CFT) description, namely, the Liouville theory coupled to the (2,p) minimal matter in the p→∞ limit. In the Liouville CFT description, the replica wormholes are created by the twist operators and the gravitational part of the bulk entanglement entropy can be reproduced from the twist operator correlators. We propose the precise dictionary and show how this correspondence works in detail.
Many density estimation techniques for 3D human motion prediction require a
significant amount of inference time, often exceeding the duration of the
predicted time horizon. To address the need for faster density estimation for
3D human motion prediction, we introduce a novel flow-based method for human
motion prediction called CacheFlow. Unlike previous conditional generative
models that suffer from time efficiency, CacheFlow takes advantage of an
unconditional flow-based generative model that transforms a Gaussian mixture
into the density of future motions. The results of the computation of the
flow-based generative model can be precomputed and cached. Then, for
conditional prediction, we seek a mapping from historical trajectories to
samples in the Gaussian mixture. This mapping can be done by a much more
lightweight model, thus saving significant computation overhead compared to a
typical conditional flow model. In such a two-stage fashion and by caching
results from the slow flow model computation, we build our CacheFlow without
loss of prediction accuracy and model expressiveness. This inference process is
completed in approximately one millisecond, making it 4 times faster than
previous VAE methods and 30 times faster than previous diffusion-based methods
on standard benchmarks such as Human3.6M and AMASS datasets. Furthermore, our
method demonstrates improved density estimation accuracy and comparable
prediction accuracy to a SOTA method on Human3.6M. Our code and models will be
publicly available.
This paper proposes a mask optimization method for improving the quality of
object removal using image inpainting. While many inpainting methods are
trained with a set of random masks, a target for inpainting may be an object,
such as a person, in many realistic scenarios. This domain gap between masks in
training and inference images increases the difficulty of the inpainting task.
In our method, this domain gap is resolved by training the inpainting network
with object masks extracted by segmentation, and such object masks are also
used in the inference step. Furthermore, to optimize the object masks for
inpainting, the segmentation network is connected to the inpainting network and
end-to-end trained to improve the inpainting performance. The effect of this
end-to-end training is further enhanced by our mask expansion loss for
achieving the trade-off between large and small masks. Experimental results
demonstrate the effectiveness of our method for better object removal using
image inpainting.
Small Object Detection (SOD) is an important machine vision topic because (i) a variety of real-world applications require object detection for distant objects and (ii) SOD is a challenging task due to the noisy, blurred, and less-informative image appearances of small objects. This paper proposes a new SOD dataset consisting of 39,070 images including 137,121 bird instances, which is called the Small Object Detection for Spotting Birds (SOD4SB) dataset. The detail of the challenge with the SOD4SB dataset is introduced in this paper. In total, 223 participants joined this challenge. This paper briefly introduces the award-winning methods. The dataset, the baseline code, and the website for evaluation on the public testset are publicly available.
While burst LR images are useful for improving the SR image quality compared with a single LR image, prior SR networks accepting the burst LR images are trained in a deterministic manner, which is known to produce a blurry SR image. In addition, it is difficult to perfectly align the burst LR images, making the SR image more blurry. Since such blurry images are perceptually degraded, we aim to reconstruct the sharp high-fidelity boundaries. Such high-fidelity images can be reconstructed by diffusion models. However, prior SR methods using the diffusion model are not properly optimized for the burst SR task. Specifically, the reverse process starting from a random sample is not optimized for image enhancement and restoration methods, including burst SR. In our proposed method, on the other hand, burst LR features are used to reconstruct the initial burst SR image that is fed into an intermediate step in the diffusion model. This reverse process from the intermediate step 1) skips diffusion steps for reconstructing the global structure of the image and 2) focuses on steps for refining detailed textures. Our experimental results demonstrate that our method can improve the scores of the perceptual quality metrics. Code: this https URL
We present a novel end-to-end neural model to extract entities and relations between them. Our recurrent neural network based model captures both word sequence and dependency tree substructure information by stacking bidirectional tree-structured LSTM-RNNs on bidirectional sequential LSTM-RNNs. This allows our model to jointly represent both entities and relations with shared parameters in a single model. We further encourage detection of entities during training and use of entity information in relation extraction via entity pretraining and scheduled sampling. Our model improves over the state-of-the-art feature-based model on end-to-end relation extraction, achieving 12.1% and 5.7% relative error reductions in F1-score on ACE2005 and ACE2004, respectively. We also show that our LSTM-RNN based model compares favorably to the state-of-the-art CNN based model (in F1-score) on nominal relation classification (SemEval-2010 Task 8). Finally, we present an extensive ablation analysis of several model components.
We proposed a novel architecture for the problem of video super-resolution. We integrate spatial and temporal contexts from continuous video frames using a recurrent encoder-decoder module, that fuses multi-frame information with the more traditional, single frame super-resolution path for the target frame. In contrast to most prior work where frames are pooled together by stacking or warping, our model, the Recurrent Back-Projection Network (RBPN) treats each context frame as a separate source of information. These sources are combined in an iterative refinement framework inspired by the idea of back-projection in multiple-image super-resolution. This is aided by explicitly representing estimated inter-frame motion with respect to the target, rather than explicitly aligning frames. We propose a new video super-resolution benchmark, allowing evaluation at a larger scale and considering videos in different motion regimes. Experimental results demonstrate that our RBPN is superior to existing methods on several datasets.
There are no more papers matching your filters at the moment.