Recent advances in reinforcement learning (RL) for large language model (LLM) fine-tuning show promise in addressing multi-objective tasks but still face significant challenges, including competing objective balancing, low training efficiency, poor scalability, and limited explainability. Leveraging ensemble learning principles, we introduce an Ensemble Multi-Objective RL (EMORL) framework that fine-tunes multiple models with individual objectives while optimizing their aggregation after the fine-tuning to improve efficiency and flexibility. Our method is the first to aggregate the hidden states of individual models, incorporating contextual information from multiple objectives. This approach is supported by a hierarchical grid search algorithm that identifies optimal weighted combinations. We evaluate EMORL on counselor reflection generation tasks, using text classification models to score the generations and provide rewards during RL fine-tuning. Through comprehensive experiments on the PAIR and Psych8k datasets, we demonstrate the advantages of EMORL against existing baselines: significantly lower and more stable training consumption ($17,529\pm 1,650$ data points and $6,573\pm 147.43$ seconds), improved scalability and explainability, and comparable performance across multiple objectives.

Large Language Models (LLMs) are rapidly transforming various fields, and their potential in Business Process Management (BPM) is substantial. This paper assesses the capabilities of LLMs on business process modeling using a framework for automating this task, a comprehensive benchmark, and an analysis of LLM self-improvement strategies. We present a comprehensive evaluation of 16 state-of-the-art LLMs from major AI vendors using a custom-designed benchmark of 20 diverse business processes. Our analysis highlights significant performance variations across LLMs and reveals a positive correlation between efficient error handling and the quality of generated models. It also shows consistent performance trends within similar LLM groups. Furthermore, we investigate LLM self-improvement techniques, encompassing self-evaluation, input optimization, and output optimization. Our findings indicate that output optimization, in particular, offers promising potential for enhancing quality, especially in models with initially lower performance. Our contributions provide insights for leveraging LLMs in BPM, paving the way for more advanced and automated process modeling techniques.

Generative AI (GenAI) is increasingly used in survey contexts to simulate human preferences. While many research endeavors evaluate the quality of synthetic GenAI data by comparing model-generated responses to gold-standard survey results, fundamental questions about the validity and reliability of using LLMs as substitutes for human respondents remain. Our study provides a technical analysis of how demographic attributes and prompt variations influence latent opinion mappings in large language models (LLMs) and evaluates their suitability for survey-based predictions. Using 14 different models, we find that LLM-generated data fails to replicate the variance observed in real-world human responses, particularly across demographic subgroups. In the political space, persona-to-party mappings exhibit limited differentiation, resulting in synthetic data that lacks the nuanced distribution of opinions found in survey data. Moreover, we show that prompt sensitivity can significantly alter outputs for some models, further undermining the stability and predictiveness of LLM-based simulations. As a key contribution, we adapt a probe-based methodology that reveals how LLMs encode political affiliations in their latent space, exposing the systematic distortions introduced by these models. Our findings highlight critical limitations in AI-generated survey data, urging caution in its use for public opinion research, social science experimentation, and computational behavioral modeling.

Customers' reviews and feedback play crucial role on electronic commerce~(E-commerce) platforms like Amazon, Zalando, and eBay in influencing other customers' purchasing decisions. However, there is a prevailing concern that sellers often post fake or spam reviews to deceive potential customers and manipulate their opinions about a product. Over the past decade, there has been considerable interest in using machine learning (ML) and deep learning (DL) models to identify such fraudulent reviews. Unfortunately, the decisions made by complex ML and DL models - which often function as \emph{black-boxes} - can be surprising and difficult for general users to comprehend. In this paper, we propose an explainable framework for detecting fake reviews with high precision in identifying fraudulent content with explanations and investigate what information matters most for explaining particular decisions by conducting empirical user evaluation. Initially, we develop fake review detection models using DL and transformer models including XLNet and DistilBERT. We then introduce layer-wise relevance propagation (LRP) technique for generating explanations that can map the contributions of words toward the predicted class. The experimental results on two benchmark fake review detection datasets demonstrate that our predictive models achieve state-of-the-art performance and outperform several existing methods. Furthermore, the empirical user evaluation of the generated explanations concludes which important information needs to be considered in generating explanations in the context of fake review identification.

Multi-Objective Reinforcement Learning (MORL) presents significant challenges and opportunities for optimizing multiple objectives in Large Language Models (LLMs). We introduce a MORL taxonomy and examine the advantages and limitations of various MORL methods when applied to LLM optimization, identifying the need for efficient and flexible approaches that accommodate personalization functionality and inherent complexities in LLMs and RL. We propose a vision for a MORL benchmarking framework that addresses the effects of different methods on diverse objective relationships. As future research directions, we focus on meta-policy MORL development that can improve efficiency and flexibility through its bi-level learning paradigm, highlighting key research questions and potential solutions for improving LLM performance.

Recent technological advancements have led to a large number of patents in a diverse range of domains, making it challenging for human experts to analyze and manage. State-of-the-art methods for multi-label patent classification rely on deep neural networks (DNNs), which are complex and often considered black-boxes due to their opaque decision-making processes. In this paper, we propose a novel deep explainable patent classification framework by introducing layer-wise relevance propagation (LRP) to provide human-understandable explanations for predictions. We train several DNN models, including Bi-LSTM, CNN, and CNN-BiLSTM, and propagate the predictions backward from the output layer up to the input layer of the model to identify the relevance of words for individual predictions. Considering the relevance score, we then generate explanations by visualizing relevant words for the predicted patent class. Experimental results on two datasets comprising two-million patent texts demonstrate high performance in terms of various evaluation measures. The explanations generated for each prediction highlight important relevant words that align with the predicted class, making the prediction more understandable. Explainable systems have the potential to facilitate the adoption of complex AI-enabled methods for patent classification in real-world applications.

Dataspaces have recently gained adoption across various sectors, including traditionally less digitized domains such as culture. Leveraging Semantic Web technologies helps to make dataspaces FAIR, but their complexity poses a significant challenge to the adoption of dataspaces and increases their cost. The advent of Large Language Models (LLMs) raises the question of how these models can support the adoption of FAIR dataspaces. In this work, we demonstrate the potential of LLMs in dataspaces with a concrete example. We also derive a research agenda for exploring this emerging field.

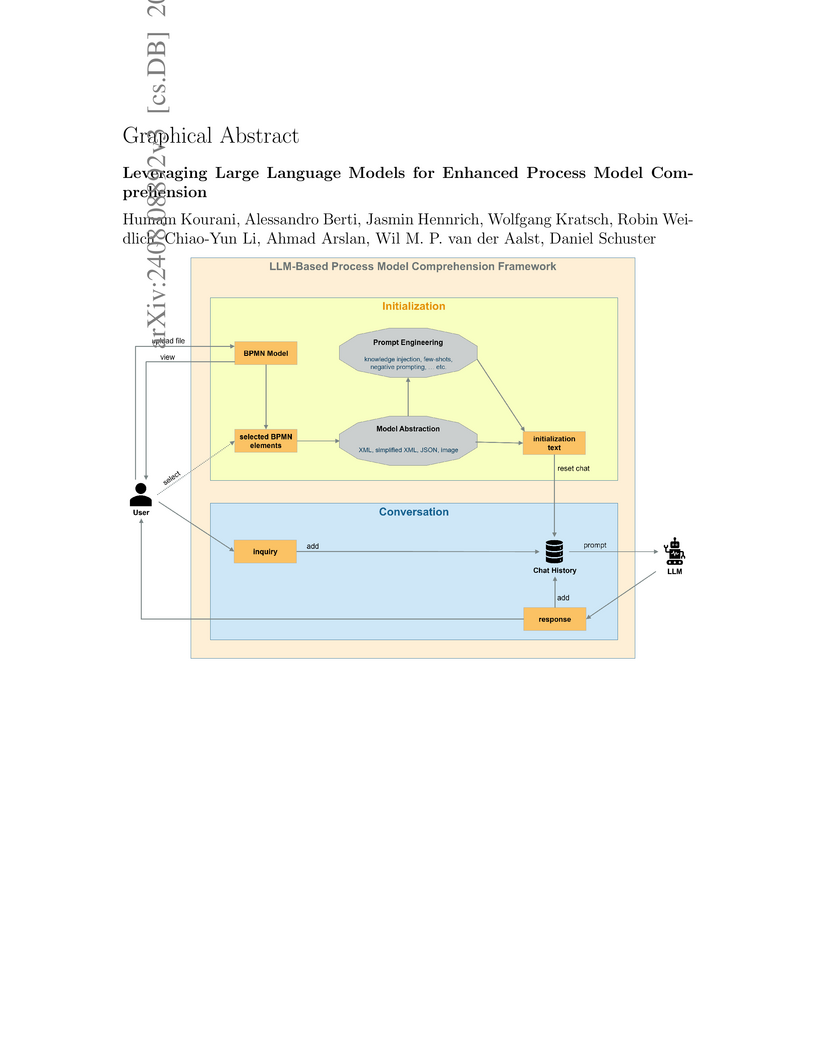
In Business Process Management (BPM), effectively comprehending process models is crucial yet poses significant challenges, particularly as organizations scale and processes become more complex. This paper introduces a novel framework utilizing the advanced capabilities of Large Language Models (LLMs) to enhance the interpretability of complex process models. We present different methods for abstracting business process models into a format accessible to LLMs, and we implement advanced prompting strategies specifically designed to optimize LLM performance within our framework. Additionally, we present a tool, AIPA, that implements our proposed framework and allows for conversational process querying. We evaluate our framework and tool by i) an automatic evaluation comparing different LLMs, model abstractions, and prompting strategies and ii) a user study designed to assess AIPA's effectiveness comprehensively. Results demonstrate our framework's ability to improve the accessibility and interpretability of process models, pioneering new pathways for integrating AI technologies into the BPM field.

Textual entailment recognition is one of the basic natural language understanding(NLU) tasks. Understanding the meaning of sentences is a prerequisite before applying any natural language processing(NLP) techniques to automatically recognize the textual entailment. A text entails a hypothesis if and only if the true value of the hypothesis follows the text. Classical approaches generally utilize the feature value of each word from word embedding to represent the sentences. In this paper, we propose a novel approach to identifying the textual entailment relationship between text and hypothesis, thereby introducing a new semantic feature focusing on empirical threshold-based semantic text representation. We employ an element-wise Manhattan distance vector-based feature that can identify the semantic entailment relationship between the text-hypothesis pair. We carried out several experiments on a benchmark entailment classification(SICK-RTE) dataset. We train several machine learning(ML) algorithms applying both semantic and lexical features to classify the text-hypothesis pair as entailment, neutral, or contradiction. Our empirical sentence representation technique enriches the semantic information of the texts and hypotheses found to be more efficient than the classical ones. In the end, our approach significantly outperforms known methods in understanding the meaning of the sentences for the textual entailment classification task.

Integrated and efficient mobility requires data sharing among the involved stakeholders. In this direction, regulators and transport authorities have been defining policies to foster the digitalisation and online publication of mobility data. However, the creation of several heterogeneous data portals for mobility data resulted in a fragmented ecosystem that challenges data accessibility. In this context, metadata is a key enabler to foster the findability and reusability of relevant datasets, but their interoperability across different data portals should be ensured. Moreover, each domain presents specificities on the relevant information that should be encoded through metadata. To solve these issues within the mobility domain, we present mobilityDCAT-AP, a reference metadata specification for mobility data portals specified by putting together domain experts and the Semantic Web community. We report on the work done to develop the metadata model behind mobilityDCAT-AP and the best practices followed in its implementation and publication. Finally, we describe the available educational resources and the activities performed to ensure broader adoption of mobilityDCAT-AP across mobility data portals. We present success stories from early adopters and discuss the challenges they encountered in implementing a metadata specification based on Semantic Web technologies.

Since their recent introduction, process trees have been frequently used as a process modeling formalism in many process mining algorithms. A process tree is a tree-based model of a process, in which internal vertices represent behavioral control-flow relations and leaves represent process activities. A process tree is easily translated into a sound Workflow net (WF-net), however, the reverse is not the case. Yet, an algorithm that translates a WF-net into a process tree is of great interest, e.g., the explicit knowledge of the control-flow hierarchy in a WF-net allows one to more easily reason on its behavior. Hence, in this paper, we present such an algorithm, i.e., it detects whether a WF-net corresponds to a process tree, and, if so, constructs it. We prove that, if a process tree is discovered, the language of the process tree equals the language of the original WF-net. Conducted experiments show, that the algorithm's corresponding implementation has a quadratic time-complexity in the size of the WF-net. Furthermore, the experiments show strong evidence of process tree rediscoverability.

Rapidly changing business environments expose companies to high levels of uncertainty. This uncertainty manifests itself in significant changes that tend to occur over the lifetime of a process and possibly affect its performance. It is important to understand the root causes of such changes since this allows us to react to change or anticipate future changes. Research in process mining has so far only focused on detecting, locating and characterizing significant changes in a process and not on finding root causes of such changes. In this paper, we aim to close this gap. We propose a framework that adds an explainability level onto concept drift detection in process mining and provides insights into the cause-effect relationships behind significant changes. We define different perspectives of a process, detect concept drifts in these perspectives and plug the perspectives into a causality check that determines whether these concept drifts can be causal to each other. We showcase the effectiveness of our framework by evaluating it on both synthetic and real event data. Our experiments show that our approach unravels cause-effect relationships and provides novel insights into executed processes.

Addressing the complexity of accurately classifying International Classification of Diseases (ICD) codes from medical discharge summaries is challenging due to the intricate nature of medical documentation. This paper explores the use of Large Language Models (LLM), specifically the LLAMA architecture, to enhance ICD code classification through two methodologies: direct application as a classifier and as a generator of enriched text representations within a Multi-Filter Residual Convolutional Neural Network (MultiResCNN) framework. We evaluate these methods by comparing them against state-of-the-art approaches, revealing LLAMA's potential to significantly improve classification outcomes by providing deep contextual insights into medical texts.

Large Language Models (LLMs) have demonstrated outstanding performance across a range of NLP tasks, however, their computational demands hinder their deployment in real-world, resource-constrained environments. This work investigates the extent to which LLMs can be compressed using Knowledge Distillation (KD) while maintaining strong performance on Question Answering (QA) tasks. We evaluate student models distilled from the Pythia and Qwen2.5 families on two QA benchmarks, SQuAD and MLQA, under zero-shot and one-shot prompting conditions. Results show that student models retain over 90% of their teacher models' performance while reducing parameter counts by up to 57.1%. Furthermore, one-shot prompting yields additional performance gains over zero-shot setups for both model families. These findings underscore the trade-off between model efficiency and task performance, demonstrating that KD, combined with minimal prompting, can yield compact yet capable QA systems suitable for resource-constrained applications.

Dataspaces are designed to support sovereign, trusted and decentralized data exchange between participants forming an ecosystem. They are standardized by initiatives such as the International Data Spaces Association or Gaia-X and have gained adoption in several domains such as mobility, manufacturing, tourism or culture. In dataspaces, participants use connectors to communicate peer-to-peer. The Eclipse Dataspace Components (EDC) Connector is a broadly adopted, open-source implementation that adheres to the standards and is supported by a large community. As dataspaces in general, it focuses on the exchange of data assets with associated usage policies and does not support services. In practice, however, there is demand for dataspace-based services and conceptual arguments support their inclusion in dataspaces. In this paper, we propose an abstraction layer for providing generic services within dataspaces. Adopters can use this layer to easily develop own services, seamlessly integrated with the existing dataspace technology. Besides, we present an initial implementation of this service architecture for the EDC Connector and demonstrate its practical applicability.

Wikipedia serves as a globally accessible knowledge source with content in over 300 languages. Despite covering the same topics, the different versions of Wikipedia are written and updated independently. This leads to factual inconsistencies that can impact the neutrality and reliability of the encyclopedia and AI systems, which often rely on Wikipedia as a main training source. This study investigates cross-lingual inconsistencies in Wikipedia's structured content, with a focus on tabular data. We developed a methodology to collect, align, and analyze tables from Wikipedia multilingual articles, defining categories of inconsistency. We apply various quantitative and qualitative metrics to assess multilingual alignment using a sample dataset. These insights have implications for factual verification, multilingual knowledge interaction, and design for reliable AI systems leveraging Wikipedia content.