Eurécom
In this paper, we propose two new performance metrics, coined the Version
Innovation Age (VIA) and the Age of Incorrect Version (AoIV) for real-time
monitoring of a two-state Markov process over an unreliable channel. We analyze
their performance under the change-aware, semantics-aware, and randomized
stationary sampling and transmission policies. We derive closed-form
expressions for the distribution and the average of VIA, AoIV, and AoII for
these policies. We then formulate and solve an optimization problem to minimize
the average VIA, subject to constraints on the time-averaged sampling cost and
time-averaged reconstruction error. Finally, we compare the performance of
various sampling and transmission policies and identify the conditions under
which each policy outperforms the others in optimizing the proposed metrics.
This research establishes a formal equivalence between autoregressive transformer-based Large Language Models (LLMs) and finite-state Markov chains. Leveraging this framework, it provides theoretical explanations for common LLM pathological behaviors, such as repetitions and reduced coherence at high temperatures, and derives generalization bounds for both pre-training and in-context learning under realistic data assumptions.
 University of TorontoWuhan University
University of TorontoWuhan University Chinese Academy of Sciences
Chinese Academy of Sciences Imperial College LondonUniversity of ZurichSungkyunkwan University
Imperial College LondonUniversity of ZurichSungkyunkwan University Shanghai Jiao Tong UniversityHarbin Institute of TechnologyPeng Cheng LaboratoryUniversitat Pompeu FabraHarvard Medical School
Shanghai Jiao Tong UniversityHarbin Institute of TechnologyPeng Cheng LaboratoryUniversitat Pompeu FabraHarvard Medical School Technical University of MunichHelmholtz MunichXiamen University of TechnologyZurich University of Applied SciencesAGH University of KrakowUniversity Hospital of ZurichUniversitat de GironaUMC UtrechtUniversity of Texas Health Science Center at HoustonNational University HospitalPeking University Health Science CenterHES-SO Valais-WallisGeneva University HospitalsHelmholtz CenterUniversity of BerneUniversity Hospital BerneHangzhou Genlight Medtech Co. Ltd.Universitat de MontrealShanghai MediWorks Precision Instruments Co.,LtdEurécom
Technical University of MunichHelmholtz MunichXiamen University of TechnologyZurich University of Applied SciencesAGH University of KrakowUniversity Hospital of ZurichUniversitat de GironaUMC UtrechtUniversity of Texas Health Science Center at HoustonNational University HospitalPeking University Health Science CenterHES-SO Valais-WallisGeneva University HospitalsHelmholtz CenterUniversity of BerneUniversity Hospital BerneHangzhou Genlight Medtech Co. Ltd.Universitat de MontrealShanghai MediWorks Precision Instruments Co.,LtdEurécomThe Circle of Willis (CoW) is an important network of arteries connecting major circulations of the brain. Its vascular architecture is believed to affect the risk, severity, and clinical outcome of serious neurovascular diseases. However, characterizing the highly variable CoW anatomy is still a manual and time-consuming expert task. The CoW is usually imaged by two non-invasive angiographic imaging modalities, magnetic resonance angiography (MRA) and computed tomography angiography (CTA), but there exist limited datasets with annotations on CoW anatomy, especially for CTA. Therefore, we organized the TopCoW challenge with the release of an annotated CoW dataset. The TopCoW dataset is the first public dataset with voxel-level annotations for 13 CoW vessel components, enabled by virtual reality technology. It is also the first large dataset using 200 pairs of MRA and CTA from the same patients. As part of the benchmark, we invited submissions worldwide and attracted over 250 registered participants from six continents. The submissions were evaluated on both internal and external test datasets of 226 scans from over five centers. The top performing teams achieved over 90% Dice scores at segmenting the CoW components, over 80% F1 scores at detecting key CoW components, and over 70% balanced accuracy at classifying CoW variants for nearly all test sets. The best algorithms also showed clinical potential in classifying fetal-type posterior cerebral artery and locating aneurysms with CoW anatomy. TopCoW demonstrated the utility and versatility of CoW segmentation algorithms for a wide range of downstream clinical applications with explainability. The annotated datasets and best performing algorithms have been released as public Zenodo records to foster further methodological development and clinical tool building.
Researchers from Aily Labs and EURECOM developed an LLM-based framework that automatically generates concise, textual insights from complex, multi-table databases using a hierarchical question generation approach. The system demonstrated superior insightfulness compared to existing automated tools while maintaining high factual correctness and reducing insight generation costs to an estimated $0.637 per insight.
Generative models form the backbone of modern machine learning, underpinning state-of-the-art systems in text, vision, and multimodal applications. While Maximum Likelihood Estimation has traditionally served as the dominant training paradigm, recent work have highlighted its limitations, particularly in generalization and susceptibility to catastrophic forgetting compared to Reinforcement Learning techniques, such as Policy Gradient methods. However, these approaches depend on explicit reward signals, which are often unavailable in practice, leaving open the fundamental problem of how to align generative models when only high-quality datasets are accessible. In this work, we address this challenge via a Bilevel Optimization framework, where the reward function is treated as the optimization variable of an outer-level problem, while a policy gradient objective defines the inner-level. We then conduct a theoretical analysis of this optimization problem in a tractable setting and extract insights that, as we demonstrate, generalize to applications such as tabular classification and model-based reinforcement learning. We release the code at this https URL .
The performance of spoofing countermeasure systems depends fundamentally upon
the use of sufficiently representative training data. With this usually being
limited, current solutions typically lack generalisation to attacks encountered
in the wild. Strategies to improve reliability in the face of uncontrolled,
unpredictable attacks are hence needed. We report in this paper our efforts to
use self-supervised learning in the form of a wav2vec 2.0 front-end with fine
tuning. Despite initial base representations being learned using only bona fide
data and no spoofed data, we obtain the lowest equal error rates reported in
the literature for both the ASVspoof 2021 Logical Access and Deepfake
databases. When combined with data augmentation,these results correspond to an
improvement of almost 90% relative to our baseline system.
27 Apr 2025
Large Language Models (LLMs) have shown impressive capabilities in
transforming natural language questions about relational databases into SQL
queries. Despite recent improvements, small LLMs struggle to handle questions
involving multiple tables and complex SQL patterns under a Zero-Shot Learning
(ZSL) setting. Supervised Fine-Tuning (SFT) partially compensates for the
knowledge deficits in pretrained models but falls short while dealing with
queries involving multi-hop reasoning. To bridge this gap, different LLM
training strategies to reinforce reasoning capabilities have been proposed,
ranging from leveraging a thinking process within ZSL, including reasoning
traces in SFT, or adopt Reinforcement Learning (RL) strategies. However, the
influence of reasoning on Text2SQL performance is still largely unexplored.
This paper investigates to what extent LLM reasoning capabilities influence
their Text2SQL performance on four benchmark datasets. To this end, it
considers the following LLM settings: (1) ZSL, including general-purpose
reasoning or not; (2) SFT, with and without task-specific reasoning traces; (3)
RL, exploring the use of different rewarding functions, both the established
EXecution accuracy (EX) and a mix with fine-grained ones that also account the
precision, recall, and cardinality of partially correct answers; (4) SFT+RL,
i.e, a two-stage approach that combines SFT and RL. The results show that
general-purpose reasoning under ZSL proves to be ineffective in tackling
complex Text2SQL cases. Small LLMs benefit from SFT with reasoning much more
than larger ones. RL is generally beneficial across all tested models and
datasets. The use of the fine-grained metrics turns out to be the most
effective RL strategy. Thanks to RL and the novel text2SQL rewards, the 7B
Qwen-Coder-2.5 model performs on par with 400+ Billion ones (including gpt-4o)
on the Bird dataset.
06 Nov 2025
Model and hyperparameter selection are critical but challenging in machine learning, typically requiring expert intuition or expensive automated search. We investigate whether large language models (LLMs) can act as in-context meta-learners for this task. By converting each dataset into interpretable metadata, we prompt an LLM to recommend both model families and hyperparameters. We study two prompting strategies: (1) a zero-shot mode relying solely on pretrained knowledge, and (2) a meta-informed mode augmented with examples of models and their performance on past tasks. Across synthetic and real-world benchmarks, we show that LLMs can exploit dataset metadata to recommend competitive models and hyperparameters without search, and that improvements from meta-informed prompting demonstrate their capacity for in-context meta-learning. These results highlight a promising new role for LLMs as lightweight, general-purpose assistants for model selection and hyperparameter optimization.
An adapted RawNet2 architecture is developed for end-to-end anti-spoofing, demonstrating superior detection of the challenging A17 neural network voice conversion attack and achieving among the best overall performance on ASVspoof 2019 when fused with a traditional LFCC-GMM system.
This paper introduces SpoofCeleb, a dataset designed for Speech Deepfake
Detection (SDD) and Spoofing-robust Automatic Speaker Verification (SASV),
utilizing source data from real-world conditions and spoofing attacks generated
by Text-To-Speech (TTS) systems also trained on the same real-world data.
Robust recognition systems require speech data recorded in varied acoustic
environments with different levels of noise to be trained. However, current
datasets typically include clean, high-quality recordings (bona fide data) due
to the requirements for TTS training; studio-quality or well-recorded read
speech is typically necessary to train TTS models. Current SDD datasets also
have limited usefulness for training SASV models due to insufficient speaker
diversity. SpoofCeleb leverages a fully automated pipeline we developed that
processes the VoxCeleb1 dataset, transforming it into a suitable form for TTS
training. We subsequently train 23 contemporary TTS systems. SpoofCeleb
comprises over 2.5 million utterances from 1,251 unique speakers, collected
under natural, real-world conditions. The dataset includes carefully
partitioned training, validation, and evaluation sets with well-controlled
experimental protocols. We present the baseline results for both SDD and SASV
tasks. All data, protocols, and baselines are publicly available at
this https URL
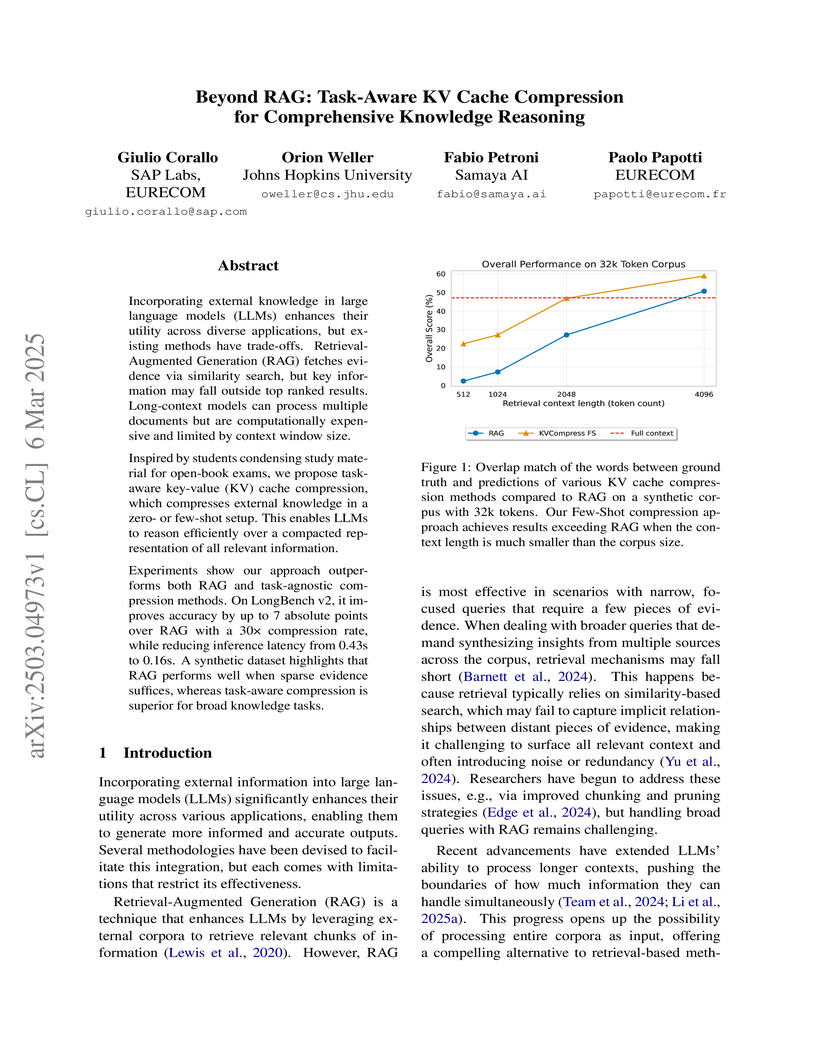
Researchers from SAP Labs, Johns Hopkins, and EURECOM introduce a novel task-aware KV cache compression technique that enables more efficient knowledge reasoning in LLMs, achieving up to 2x faster inference than RAG while maintaining superior performance on complex multi-hop queries through innovative pre-computed compressed caches tailored to specific task domains.
13 Feb 2025
Researchers from Huawei Noah’s Ark Lab and academic institutions developed a method for Large Language Models (LLMs) to predict the dynamics of continuous Markov Decision Processes (MDPs) in a zero-shot manner. Their Disentangled In-Context Learning (DICL) framework, which leverages PCA to manage multivariate data, improves prediction accuracy and enhances sample efficiency in model-based reinforcement learning.
Northwestern Polytechnical University Northeastern University
Northeastern University Sun Yat-Sen UniversityGhent UniversityKorea University
Sun Yat-Sen UniversityGhent UniversityKorea University Nanjing University
Nanjing University Zhejiang University
Zhejiang University University of MichiganXidian UniversityUniversity of Electronic Science and Technology of ChinaCentral South UniversityUniversity of Hong KongTechnology Innovation Institute
University of MichiganXidian UniversityUniversity of Electronic Science and Technology of ChinaCentral South UniversityUniversity of Hong KongTechnology Innovation Institute Yale UniversityUniversitat Pompeu Fabra
Yale UniversityUniversitat Pompeu Fabra NVIDIA
NVIDIA Huawei
Huawei Nanyang Technological UniversityUniversity of GranadaChina TelecomUlsan National Institute of Science and Technology
Nanyang Technological UniversityUniversity of GranadaChina TelecomUlsan National Institute of Science and Technology King’s College LondonSingapore University of Technology and Design
King’s College LondonSingapore University of Technology and Design Aalto University
Aalto University Virginia TechUniversity of HoustonEast China Normal University
Virginia TechUniversity of HoustonEast China Normal University KTH Royal Institute of TechnologyUniversity of OuluKhalifa UniversityLightOnCentraleSupélecUniversity of LeedsIMECNokia Bell LabsCEA-LetiUniversity of YorkOrangeEricssonBrunel University LondonQualcommChina UnicomBubbleRANITUEMIRATES INTEGRATED TELECOMMUNICATIONS COMPANYFENTECHGSMARIMEDO LABSKATIMCHINA MOBILE COMMUNICATIONS CORPORATIONBeijing Institute of TechnologyEurécom
KTH Royal Institute of TechnologyUniversity of OuluKhalifa UniversityLightOnCentraleSupélecUniversity of LeedsIMECNokia Bell LabsCEA-LetiUniversity of YorkOrangeEricssonBrunel University LondonQualcommChina UnicomBubbleRANITUEMIRATES INTEGRATED TELECOMMUNICATIONS COMPANYFENTECHGSMARIMEDO LABSKATIMCHINA MOBILE COMMUNICATIONS CORPORATIONBeijing Institute of TechnologyEurécom
 Northeastern University
Northeastern University Sun Yat-Sen UniversityGhent UniversityKorea University
Sun Yat-Sen UniversityGhent UniversityKorea University Nanjing University
Nanjing University Zhejiang University
Zhejiang University University of MichiganXidian UniversityUniversity of Electronic Science and Technology of ChinaCentral South UniversityUniversity of Hong KongTechnology Innovation Institute
University of MichiganXidian UniversityUniversity of Electronic Science and Technology of ChinaCentral South UniversityUniversity of Hong KongTechnology Innovation Institute Yale UniversityUniversitat Pompeu Fabra
Yale UniversityUniversitat Pompeu Fabra NVIDIA
NVIDIA Huawei
Huawei Nanyang Technological UniversityUniversity of GranadaChina TelecomUlsan National Institute of Science and Technology
Nanyang Technological UniversityUniversity of GranadaChina TelecomUlsan National Institute of Science and Technology King’s College LondonSingapore University of Technology and Design
King’s College LondonSingapore University of Technology and Design Aalto University
Aalto University Virginia TechUniversity of HoustonEast China Normal University
Virginia TechUniversity of HoustonEast China Normal University KTH Royal Institute of TechnologyUniversity of OuluKhalifa UniversityLightOnCentraleSupélecUniversity of LeedsIMECNokia Bell LabsCEA-LetiUniversity of YorkOrangeEricssonBrunel University LondonQualcommChina UnicomBubbleRANITUEMIRATES INTEGRATED TELECOMMUNICATIONS COMPANYFENTECHGSMARIMEDO LABSKATIMCHINA MOBILE COMMUNICATIONS CORPORATIONBeijing Institute of TechnologyEurécom
KTH Royal Institute of TechnologyUniversity of OuluKhalifa UniversityLightOnCentraleSupélecUniversity of LeedsIMECNokia Bell LabsCEA-LetiUniversity of YorkOrangeEricssonBrunel University LondonQualcommChina UnicomBubbleRANITUEMIRATES INTEGRATED TELECOMMUNICATIONS COMPANYFENTECHGSMARIMEDO LABSKATIMCHINA MOBILE COMMUNICATIONS CORPORATIONBeijing Institute of TechnologyEurécomA comprehensive white paper from the GenAINet Initiative introduces Large Telecom Models (LTMs) as a novel framework for integrating AI into telecommunications infrastructure, providing a detailed roadmap for innovation while addressing critical challenges in scalability, hardware requirements, and regulatory compliance through insights from a diverse coalition of academic, industry and regulatory experts.
In this work we present a new method for the estimation of Mutual Information (MI) between random variables. Our approach is based on an original interpretation of the Girsanov theorem, which allows us to use score-based diffusion models to estimate the Kullback Leibler divergence between two densities as a difference between their score functions. As a by-product, our method also enables the estimation of the entropy of random variables. Armed with such building blocks, we present a general recipe to measure MI, which unfolds in two directions: one uses conditional diffusion process, whereas the other uses joint diffusion processes that allow simultaneous modelling of two random variables. Our results, which derive from a thorough experimental protocol over all the variants of our approach, indicate that our method is more accurate than the main alternatives from the literature, especially for challenging distributions. Furthermore, our methods pass MI self-consistency tests, including data processing and additivity under independence, which instead are a pain-point of existing methods.
The analysis of scientific data and complex multivariate systems requires
information quantities that capture relationships among multiple random
variables. Recently, new information-theoretic measures have been developed to
overcome the shortcomings of classical ones, such as mutual information, that
are restricted to considering pairwise interactions. Among them, the concept of
information synergy and redundancy is crucial for understanding the high-order
dependencies between variables. One of the most prominent and versatile
measures based on this concept is O-information, which provides a clear and
scalable way to quantify the synergy-redundancy balance in multivariate
systems. However, its practical application is limited to simplified cases. In
this work, we introduce SΩI, which allows for the first time to compute
O-information without restrictive assumptions about the system. Our experiments
validate our approach on synthetic data, and demonstrate the effectiveness of
SΩI in the context of a real-world use case.
Traditional Text-to-Speech (TTS) systems rely on studio-quality speech
recorded in controlled settings.a Recently, an effort known as noisy-TTS
training has emerged, aiming to utilize in-the-wild data. However, the lack of
dedicated datasets has been a significant limitation. We introduce the TTS In
the Wild (TITW) dataset, which is publicly available, created through a fully
automated pipeline applied to the VoxCeleb1 dataset. It comprises two training
sets: TITW-Hard, derived from the transcription, segmentation, and selection of
raw VoxCeleb1 data, and TITW-Easy, which incorporates additional enhancement
and data selection based on DNSMOS. State-of-the-art TTS models achieve over
3.0 UTMOS score with TITW-Easy, while TITW-Hard remains difficult showing UTMOS
below 2.8.
Deep learning has recently revealed the existence of scaling laws,
demonstrating that model performance follows predictable trends based on
dataset and model sizes. Inspired by these findings and fascinating phenomena
emerging in the over-parameterized regime, we examine a parallel direction: do
similar scaling laws govern predictive uncertainties in deep learning? In
identifiable parametric models, such scaling laws can be derived in a
straightforward manner by treating model parameters in a Bayesian way. In this
case, for example, we obtain O(1/N) contraction rates for epistemic
uncertainty with respect to the number of data N. However, in
over-parameterized models, these guarantees do not hold, leading to largely
unexplored behaviors. In this work, we empirically show the existence of
scaling laws associated with various measures of predictive uncertainty with
respect to dataset and model sizes. Through experiments on vision and language
tasks, we observe such scaling laws for in- and out-of-distribution predictive
uncertainty estimated through popular approximate Bayesian inference and
ensemble methods. Besides the elegance of scaling laws and the practical
utility of extrapolating uncertainties to larger data or models, this work
provides strong evidence to dispel recurring skepticism against Bayesian
approaches: "In many applications of deep learning we have so much data
available: what do we need Bayes for?". Our findings show that "so much data"
is typically not enough to make epistemic uncertainty negligible.
This paper studies a finite-horizon Markov decision problem with information-theoretic constraints, where the goal is to minimize directed information from the controlled source process to the control process, subject to stage-wise cost constraints, aiming for an optimal control policy. We propose a new way of approximating a solution for this problem, which is known to be formulated as an unconstrained MDP with a continuous information-state using Q-factors. To avoid the computational complexity of discretizing the continuous information-state space, we propose a truncated rollout-based backward-forward approximate dynamic programming (ADP) framework. Our approach consists of two phases: an offline base policy approximation over a shorter time horizon, followed by an online rollout lookahead minimization, both supported by provable convergence guarantees. We supplement our theoretical results with a numerical example where we demonstrate the cost improvement of the rollout method compared to a previously proposed policy approximation method, and the computational complexity observed in executing the offline and online phases for the two methods.
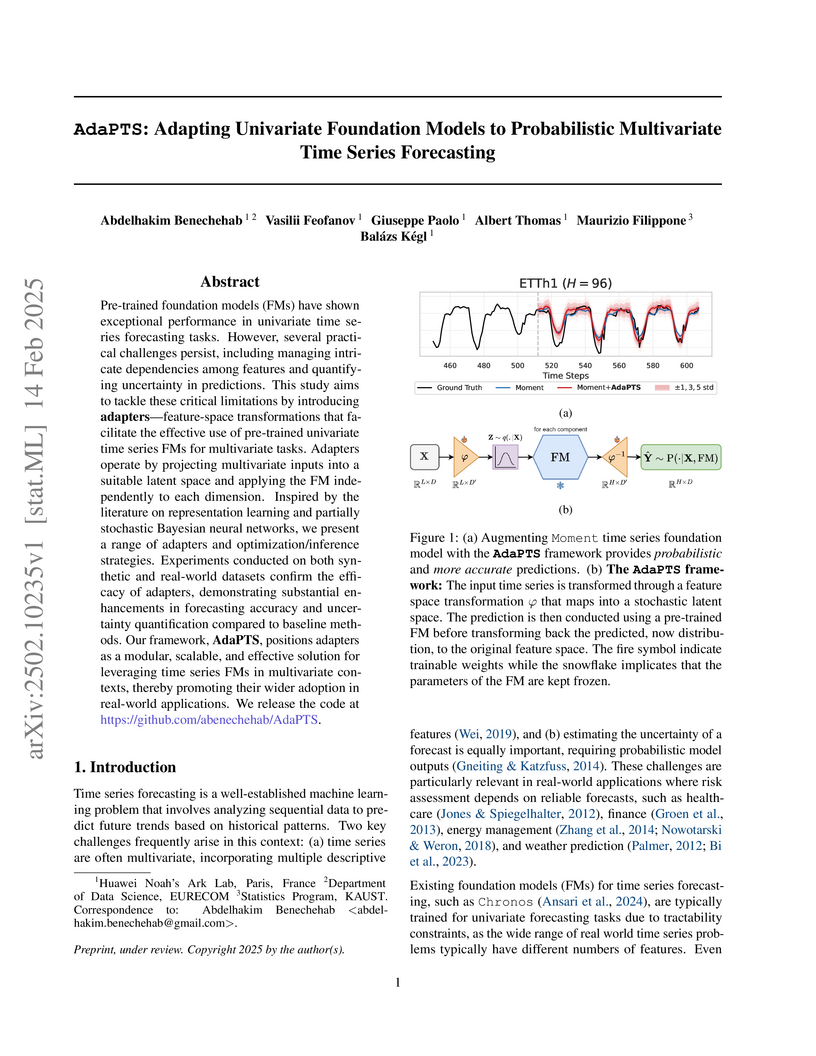
Pre-trained foundation models (FMs) have shown exceptional performance in
univariate time series forecasting tasks. However, several practical challenges
persist, including managing intricate dependencies among features and
quantifying uncertainty in predictions. This study aims to tackle these
critical limitations by introducing adapters; feature-space transformations
that facilitate the effective use of pre-trained univariate time series FMs for
multivariate tasks. Adapters operate by projecting multivariate inputs into a
suitable latent space and applying the FM independently to each dimension.
Inspired by the literature on representation learning and partially stochastic
Bayesian neural networks, we present a range of adapters and
optimization/inference strategies. Experiments conducted on both synthetic and
real-world datasets confirm the efficacy of adapters, demonstrating substantial
enhancements in forecasting accuracy and uncertainty quantification compared to
baseline methods. Our framework, AdaPTS, positions adapters as a modular,
scalable, and effective solution for leveraging time series FMs in multivariate
contexts, thereby promoting their wider adoption in real-world applications. We
release the code at this https URL
This monograph comprehensively unifies Gaussian Processes (GPs) and Reproducing Kernel Hilbert Spaces (RKHSs) by systematically demonstrating their fundamental connections through the canonical isometry between the Gaussian Hilbert Space and the RKHS. It explains how GP uncertainty can be interpreted within the RKHS framework and clarifies the properties of GP sample paths.
There are no more papers matching your filters at the moment.