Entities are at the center of how we represent and aggregate knowledge. For instance, Encyclopedias such as Wikipedia are structured by entities (e.g., one per Wikipedia article). The ability to retrieve such entities given a query is fundamental for knowledge-intensive tasks such as entity linking and open-domain question answering. Current approaches can be understood as classifiers among atomic labels, one for each entity. Their weight vectors are dense entity representations produced by encoding entity meta information such as their descriptions. This approach has several shortcomings: (i) context and entity affinity is mainly captured through a vector dot product, potentially missing fine-grained interactions; (ii) a large memory footprint is needed to store dense representations when considering large entity sets; (iii) an appropriately hard set of negative data has to be subsampled at training time. In this work, we propose GENRE, the first system that retrieves entities by generating their unique names, left to right, token-by-token in an autoregressive fashion. This mitigates the aforementioned technical issues since: (i) the autoregressive formulation directly captures relations between context and entity name, effectively cross encoding both; (ii) the memory footprint is greatly reduced because the parameters of our encoder-decoder architecture scale with vocabulary size, not entity count; (iii) the softmax loss is computed without subsampling negative data. We experiment with more than 20 datasets on entity disambiguation, end-to-end entity linking and document retrieval tasks, achieving new state-of-the-art or very competitive results while using a tiny fraction of the memory footprint of competing systems. Finally, we demonstrate that new entities can be added by simply specifying their names. Code and pre-trained models at this https URL.

Comparing metric measure spaces (i.e. a metric space endowed with aprobability distribution) is at the heart of many machine learning problems. The most popular distance between such metric measure spaces is theGromov-Wasserstein (GW) distance, which is the solution of a quadratic assignment problem. The GW distance is however limited to the comparison of metric measure spaces endowed with a probability distribution. To alleviate this issue, we introduce two Unbalanced Gromov-Wasserstein formulations: a distance and a more tractable upper-bounding relaxation.They both allow the comparison of metric spaces equipped with arbitrary positive measures up to isometries. The first formulation is a positive and definite divergence based on a relaxation of the mass conservation constraint using a novel type of quadratically-homogeneous divergence. This divergence works hand in hand with the entropic regularization approach which is popular to solve large scale optimal transport problems. We show that the underlying non-convex optimization problem can be efficiently tackled using a highly parallelizable and GPU-friendly iterative scheme. The second formulation is a distance between mm-spaces up to isometries based on a conic lifting. Lastly, we provide numerical experiments onsynthetic examples and domain adaptation data with a Positive-Unlabeled learning task to highlight the salient features of the unbalanced divergence and its potential applications in ML.

Recent neural compression methods have been based on the popular hyperprior framework. It relies on Scalar Quantization and offers a very strong compression performance. This contrasts from recent advances in image generation and representation learning, where Vector Quantization is more commonly employed. In this work, we attempt to bring these lines of research closer by revisiting vector quantization for image compression. We build upon the VQ-VAE framework and introduce several modifications. First, we replace the vanilla vector quantizer by a product quantizer. This intermediate solution between vector and scalar quantization allows for a much wider set of rate-distortion points: It implicitly defines high-quality quantizers that would otherwise require intractably large codebooks. Second, inspired by the success of Masked Image Modeling (MIM) in the context of self-supervised learning and generative image models, we propose a novel conditional entropy model which improves entropy coding by modelling the co-dependencies of the quantized latent codes. The resulting PQ-MIM model is surprisingly effective: its compression performance on par with recent hyperprior methods. It also outperforms HiFiC in terms of FID and KID metrics when optimized with perceptual losses (e.g. adversarial). Finally, since PQ-MIM is compatible with image generation frameworks, we show qualitatively that it can operate under a hybrid mode between compression and generation, with no further training or finetuning. As a result, we explore the extreme compression regime where an image is compressed into 200 bytes, i.e., less than a tweet.

Various classes of Graph Neural Networks (GNN) have been proposed and shown to be successful in a wide range of applications with graph structured data. In this paper, we propose a theoretical framework able to compare the expressive power of these GNN architectures. The current universality theorems only apply to intractable classes of GNNs. Here, we prove the first approximation guarantees for practical GNNs, paving the way for a better understanding of their generalization. Our theoretical results are proved for invariant GNNs computing a graph embedding (permutation of the nodes of the input graph does not affect the output) and equivariant GNNs computing an embedding of the nodes (permutation of the input permutes the output). We show that Folklore Graph Neural Networks (FGNN), which are tensor based GNNs augmented with matrix multiplication are the most expressive architectures proposed so far for a given tensor order. We illustrate our results on the Quadratic Assignment Problem (a NP-Hard combinatorial problem) by showing that FGNNs are able to learn how to solve the problem, leading to much better average performances than existing algorithms (based on spectral, SDP or other GNNs architectures). On a practical side, we also implement masked tensors to handle batches of graphs of varying sizes.

Originally formalized with symbolic representations, syntactic trees may also be effectively represented in the activations of large language models (LLMs). Indeed, a 'Structural Probe' can find a subspace of neural activations, where syntactically related words are relatively close to one-another. However, this syntactic code remains incomplete: the distance between the Structural Probe word embeddings can represent the existence but not the type and direction of syntactic relations. Here, we hypothesize that syntactic relations are, in fact, coded by the relative direction between nearby embeddings. To test this hypothesis, we introduce a 'Polar Probe' trained to read syntactic relations from both the distance and the direction between word embeddings. Our approach reveals three main findings. First, our Polar Probe successfully recovers the type and direction of syntactic relations, and substantially outperforms the Structural Probe by nearly two folds. Second, we confirm that this polar coordinate system exists in a low-dimensional subspace of the intermediate layers of many LLMs and becomes increasingly precise in the latest frontier models. Third, we demonstrate with a new benchmark that similar syntactic relations are coded similarly across the nested levels of syntactic trees. Overall, this work shows that LLMs spontaneously learn a geometry of neural activations that explicitly represents the main symbolic structures of linguistic theory.

Denoising diffusion models have recently emerged as a powerful class of generative models. They provide state-of-the-art results, not only for unconditional simulation, but also when used to solve conditional simulation problems arising in a wide range of inverse problems. A limitation of these models is that they are computationally intensive at generation time as they require simulating a diffusion process over a long time horizon. When performing unconditional simulation, a Schrödinger bridge formulation of generative modeling leads to a theoretically grounded algorithm shortening generation time which is complementary to other proposed acceleration techniques. We extend the Schrödinger bridge framework to conditional simulation. We demonstrate this novel methodology on various applications including image super-resolution, optimal filtering for state-space models and the refinement of pre-trained networks. Our code can be found at this https URL.

In these lecture notes, we discuss the physics of a two-dimensional binary mixture of Bose gases at zero temperature, close to the point where the two fluids tend to demix. We are interested in the case where one of the two fluids (the bath) fills the whole space, while the other one (the minority component) contains a finite number of atoms. We discuss under which condition the minority component can form a stable, localized wave packet, which we relate to the celebrated "Townes soliton". We discuss the formation of this soliton and the transition towards a droplet regime that occurs when the number of atoms in the minority component is increased. Our investigation is based on a macroscopic approach based on coupled Gross-Pitaevskii equations, and it is complemented by a microscopic analysis in terms of bath-mediated interactions between the particles of the minority component.

State-of-the-art maximum entropy models for texture synthesis are built from statistics relying on image representations defined by convolutional neural networks (CNN). Such representations capture rich structures in texture images, outperforming wavelet-based representations in this regard. However, conversely to neural networks, wavelets offer meaningful representations, as they are known to detect structures at multiple scales (e.g. edges) in images. In this work, we propose a family of statistics built upon non-linear wavelet based representations, that can be viewed as a particular instance of a one-layer CNN, using a generalized rectifier non-linearity. These statistics significantly improve the visual quality of previous classical wavelet-based models, and allow one to produce syntheses of similar quality to state-of-the-art models, on both gray-scale and color textures.

Sudden quenches in quantum many-body systems often lead to dynamical evolutions that unveil surprising physical behaviors. In this work, we argue that the emergence of weak ergodicity breaking following quantum quenches in certain local many-body systems is a direct consequence of lattice discretization. To support this claim, we investigate the out-of-equilibrium dynamics of quantum $O(n)$ models on a lattice. In doing so, we also revisit two puzzling results in the literature on quantum $O(n)$ models, concerning universal scaling and equilibration, and demonstrate how these apparent contradictions can be resolved by properly accounting for lattice effects.

Auxiliary objectives, supplementary learning signals that are introduced to help aid learning on data-starved or highly complex end-tasks, are commonplace in machine learning. Whilst much work has been done to formulate useful auxiliary objectives, their construction is still an art which proceeds by slow and tedious hand-design. Intuition for how and when these objectives improve end-task performance has also had limited theoretical backing. In this work, we present an approach for automatically generating a suite of auxiliary objectives. We achieve this by deconstructing existing objectives within a novel unified taxonomy, identifying connections between them, and generating new ones based on the uncovered structure. Next, we theoretically formalize widely-held intuitions about how auxiliary learning improves generalization on the end-task. This leads us to a principled and efficient algorithm for searching the space of generated objectives to find those most useful to a specified end-task. With natural language processing (NLP) as our domain of study, we demonstrate that our automated auxiliary learning pipeline leads to strong improvements over competitive baselines across continued training experiments on a pre-trained model on 5 NLP tasks.

In order to address increasing demands of real-world applications, the research for knowledge-intensive NLP (KI-NLP) should advance by capturing the challenges of a truly open-domain environment: web-scale knowledge, lack of structure, inconsistent quality and noise. To this end, we propose a new setup for evaluating existing knowledge intensive tasks in which we generalize the background corpus to a universal web snapshot. We investigate a slate of NLP tasks which rely on knowledge - either factual or common sense, and ask systems to use a subset of CCNet - the Sphere corpus - as a knowledge source. In contrast to Wikipedia, otherwise a common background corpus in KI-NLP, Sphere is orders of magnitude larger and better reflects the full diversity of knowledge on the web. Despite potential gaps in coverage, challenges of scale, lack of structure and lower quality, we find that retrieval from Sphere enables a state of the art system to match and even outperform Wikipedia-based models on several tasks. We also observe that while a dense index can outperform a sparse BM25 baseline on Wikipedia, on Sphere this is not yet possible. To facilitate further research and minimise the community's reliance on proprietary, black-box search engines, we share our indices, evaluation metrics and infrastructure.

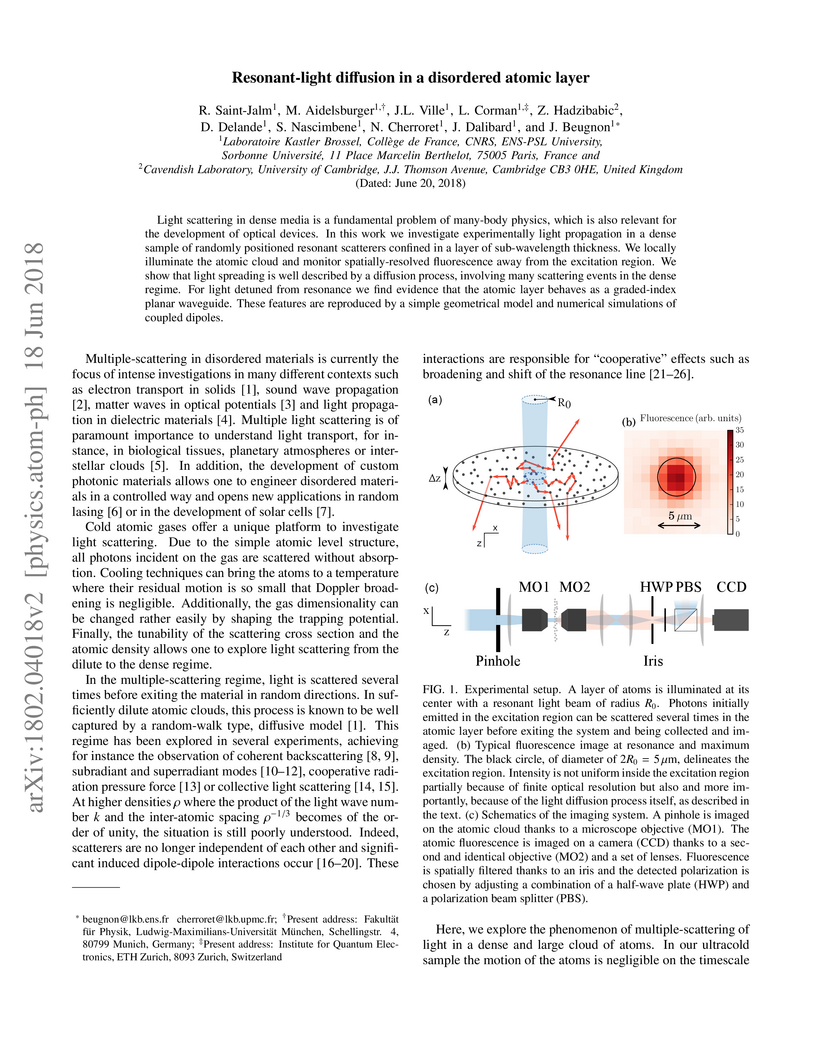
Light scattering in dense media is a fundamental problem of many-body physics, which is also relevant for the development of optical devices. In this work we investigate experimentally light propagation in a dense sample of randomly positioned resonant scatterers confined in a layer of sub-wavelength thickness. We locally illuminate the atomic cloud and monitor spatially-resolved fluorescence away from the excitation region. We show that light spreading is well described by a diffusion process, involving many scattering events in the dense regime. For light detuned from resonance we find evidence that the atomic layer behaves as a graded-index planar waveguide. These features are reproduced by a simple geometrical model and numerical simulations of coupled dipoles.

Quantum Hall states are characterized by a topological invariant, the many-body Chern number, which determines the quantized value of the Hall conductivity. Interestingly, this topological property can also be accessed through a dissipative response, by subjecting the system to a circular drive and comparing excitation rates obtained for opposite orientations of the drive. This quantized circular dichroism assumes that only the bulk contributes to the response. Indeed, in a confined and isolated system, the edge contribution exactly cancels the bulk response. This work explores an important corollary of the latter observation: If properly isolated, the circular dichroic response stemming from the edge of a quantum Hall droplet must be quantized, thus providing an appealing way to probe the many-body Chern number. Importantly, we demonstrate that this quantized edge response is entirely captured by low-energy chiral edge modes, allowing for a universal description of this effect based on Wen's edge theory. Its low-energy nature implies that the quantized edge response can be distinguished from the bulk response in the frequency domain. We illustrate our findings using realistic models of integer and fractional Chern insulators, with different edge geometries, and propose detection schemes suitable for ultracold atoms. Edge dichroic responses emerge as a practical probe for strongly-correlated topological phases, accessible in cold-atom experiments.

The motion of a quantum system subjected to an external force often defeats our classical intuition. A celebrated example is the dynamics of a single particle in a periodic potential, which undergoes Bloch oscillations under the action of a constant force. Surprisingly, Bloch-like oscillations can also occur in one-dimensional quantum fluids without requiring the presence of a lattice. The intriguing generalization of Bloch oscillations to a weakly-bounded ensemble of interacting particles has been so far limited to the experimental study of the two-particle case, where the observed period is halved compared to the single-particle case. In this work, we observe the oscillations of the position of a mesoscopic solitonic wave packet, consisting of approximately 1000 atoms in a one-dimensional Bose gas when subjected to a constant uniform force and in the absence of a lattice potential. The oscillation period scales inversely with the atom number, thus revealing its collective nature. We demonstrate the pivotal role of the phase coherence of the quantum bath in which the wave packet moves and investigate the underlying topology of the associated superfluid currents. Our measurements highlight the periodicity of the dispersion relation of collective excitations in one-dimensional quantum systems. We anticipate that our observation of such a macroscopic quantum phenomenon will inspire further studies on the crossover between classical and quantum laws of motion, such as exploring the role of dissipation, similarly to the textbook case of macroscopic quantum tunneling in Josephson physics.

We introduce and study a model in one dimension of $N$ run-and-tumble particles (RTP) which repel each other logarithmically in the presence of an external quadratic potential. This is an "active'' version of the well-known Dyson Brownian motion (DBM) where the particles are subjected to a telegraphic noise, with two possible states $\pm$ with velocity $\pm v_0$. We study analytically and numerically two different versions of this model. In model I a particle only interacts with particles in the same state, while in model II all the particles interact with each other. In the large time limit, both models converge to a steady state where the stationary density has a finite support. For finite $N$, the stationary density exhibits singularities, which disappear when $N \to +\infty$. In that limit, for model I, using a Dean-Kawasaki approach, we show that the stationary density of $+$ (respectively $-$) particles deviates from the DBM Wigner semi-circular shape, and vanishes with an exponent $3/2$ at one of the edges. In model II, the Dean-Kawasaki approach fails but we obtain strong evidence that the density in the large $N$ limit retains a Wigner semi-circular shape.

Topological quantum many-body systems, such as Hall insulators, are characterized by a hidden order encoded in the entanglement between their constituents. Entanglement entropy, an experimentally accessible single number that globally quantifies entanglement, has been proposed as a first signature of topological order. Conversely, the full description of entanglement relies on the entanglement Hamiltonian, a more complex object originally introduced to formulate quantum entanglement in curved spacetime. As conjectured by Li and Haldane, the entanglement Hamiltonian of a many-body system appears to be directly linked to its boundary properties, making it particularly useful for characterizing topological systems. While the entanglement spectrum is commonly used to identify complex phases arising in numerical simulations, its measurement remains an outstanding challenge. Here, we perform a variational approach to realize experimentally, as a genuine Hamiltonian, the entanglement Hamiltonian of a synthetic quantum Hall system. We use a synthetic dimension, encoded in the electronic spin of dysprosium atoms, to implement spatially deformed Hall systems, as suggested by the Bisognano-Wichmann prediction. The spectrum of the optimal variational Hamiltonian exhibits a chiral dispersion akin to a topological edge mode, revealing the fundamental link between entanglement and boundary physics. Our variational procedure can be easily generalized to interacting many-body systems on various platforms, marking an important step towards the exploration of exotic quantum systems with long-range correlations, such as fractional Hall states, chiral spin liquids and critical systems.

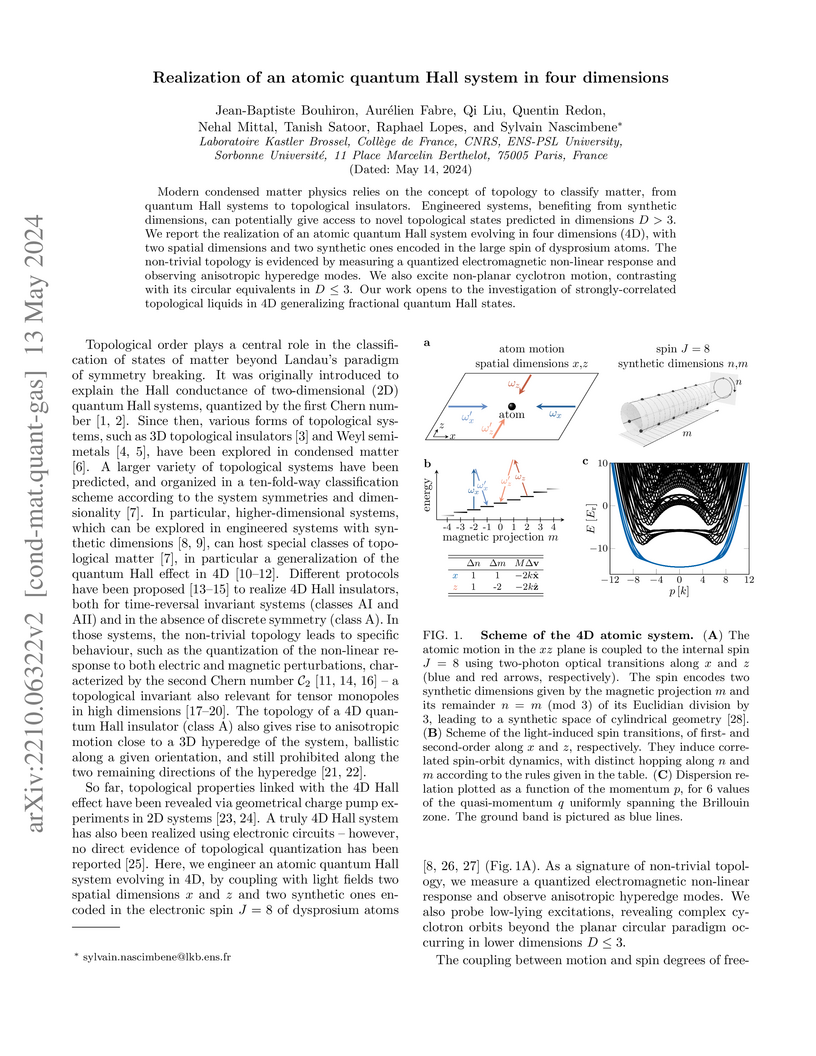
Modern condensed matter physics relies on the concept of topology to classify matter, from quantum Hall systems to topological insulators. Engineered systems, benefiting from synthetic dimensions, can potentially give access to novel topological states predicted in dimensions $D > 3$. We report the realization of an atomic quantum Hall system evolving in four dimensions (4D), with two spatial dimensions and two synthetic ones encoded in the large spin of dysprosium atoms. The non-trivial topology is evidenced by measuring a quantized electromagnetic non-linear response and observing anisotropic hyperedge modes. We also excite non-planar cyclotron motion, contrasting with its circular equivalents in $D\leq3$. Our work opens to the investigation of strongly-correlated topological liquids in 4D generalizing fractional quantum Hall states.