Inner Interpretability is a promising emerging field tasked with uncovering the inner mechanisms of AI systems, though how to develop these mechanistic theories is still much debated. Moreover, recent critiques raise issues that question its usefulness to advance the broader goals of AI. However, it has been overlooked that these issues resemble those that have been grappled with in another field: Cognitive Neuroscience. Here we draw the relevant connections and highlight lessons that can be transferred productively between fields. Based on these, we propose a general conceptual framework and give concrete methodological strategies for building mechanistic explanations in AI inner interpretability research. With this conceptual framework, Inner Interpretability can fend off critiques and position itself on a productive path to explain AI systems.

Identification of cracks is essential to assess the structural integrity of concrete infrastructure. However, robust crack segmentation remains a challenging task for computer vision systems due to the diverse appearance of concrete surfaces, variable lighting and weather conditions, and the overlapping of different defects. In particular recent data-driven methods struggle with the limited availability of data, the fine-grained and time-consuming nature of crack annotation, and face subsequent difficulty in generalizing to out-of-distribution samples. In this work, we move past these challenges in a two-fold way. We introduce a high-fidelity crack graphics simulator based on fractals and a corresponding fully-annotated crack dataset. We then complement the latter with a system that learns generalizable representations from simulation, by leveraging both a pointwise mutual information estimate along with adaptive instance normalization as inductive biases. Finally, we empirically highlight how different design choices are symbiotic in bridging the simulation to real gap, and ultimately demonstrate that our introduced system can effectively handle real-world crack segmentation.

Biological processes rely on finely tuned homo- and heteromeric interactions between (biomacro)molecules. The strength of an interaction, typically given by the dissociation constant (KD), plays a crucial role in basic research and must be monitored throughout the development of drugs and agrochemicals. An ideal method for KD determination is applicable to various analytes with a large range of affinities, tolerates complex matrix compositions, does not require labeling, and simultaneously provides information on the structural integrity of the binding partners. Native mass spectrometry meets these criteria but typically struggles with homooligomeric complexes due to overlapping mass signals. To overcome this, we resolve monomer/dimer contributions to overlapping MS-peaks by separately analyzing the charge state distribution of each oligomeric species via sample dilution and covalent crosslinking. Following this approach, we show that quantitative Laser-Induced Liquid Bead Ion Desorption mass spectrometry (qLILBID-MS) accurately captures the affinities of Bovine Serum Albumin and chemically induced dimers of Tryparedoxin, an oxidoreductase from human pathogenic Trypanosoma brucei parasites, with various molecular glues and homodimer affinities. Conveniently, qLILBID-MS requires a fraction of sample used by other methods such as isothermal titration calorimetry and yields previously inaccessible protein homodimer KDs in the high micromolar range, which allowed us to monitor the gradual decrease in homodimer affinity via mutation of crucial dimer interface contacts. Overall, qLILBID-MS is a sensitive, robust, fast, scalable, and cost-effective alternative to quantify protein/protein interactions that can accelerate contemporary drug discovery workflows, e.g. the efficient screening for proximity inducing molecules like proteolysis targeting chimera and molecular glues.

Many proposed applications of neural networks in machine learning, cognitive/brain science, and society hinge on the feasibility of inner interpretability via circuit discovery. This calls for empirical and theoretical explorations of viable algorithmic options. Despite advances in the design and testing of heuristics, there are concerns about their scalability and faithfulness at a time when we lack understanding of the complexity properties of the problems they are deployed to solve. To address this, we study circuit discovery with classical and parameterized computational complexity theory: (1) we describe a conceptual scaffolding to reason about circuit finding queries in terms of affordances for description, explanation, prediction and control; (2) we formalize a comprehensive set of queries for mechanistic explanation, and propose a formal framework for their analysis; (3) we use it to settle the complexity of many query variants and relaxations of practical interest on multi-layer perceptrons. Our findings reveal a challenging complexity landscape. Many queries are intractable, remain fixed-parameter intractable relative to model/circuit features, and inapproximable under additive, multiplicative, and probabilistic approximation schemes. To navigate this landscape, we prove there exist transformations to tackle some of these hard problems with better-understood heuristics, and prove the tractability or fixed-parameter tractability of more modest queries which retain useful affordances. This framework allows us to understand the scope and limits of interpretability queries, explore viable options, and compare their resource demands on existing and future architectures.

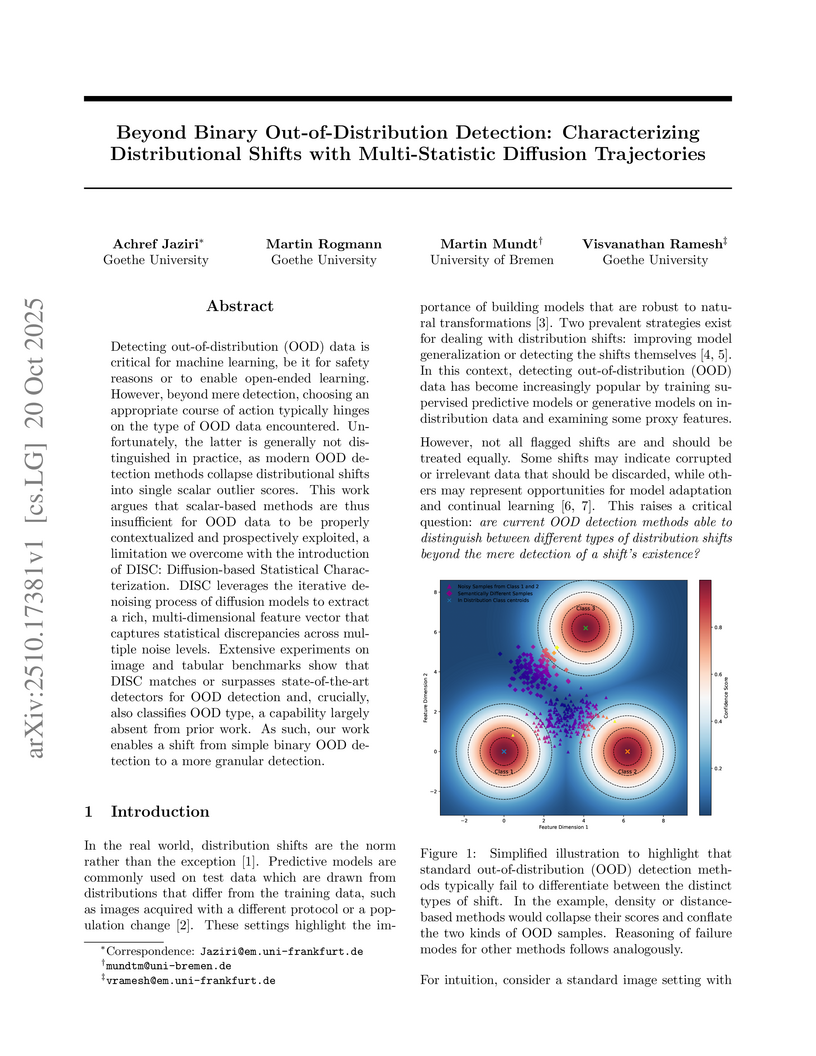
Detecting out-of-distribution (OOD) data is critical for machine learning, be it for safety reasons or to enable open-ended learning. However, beyond mere detection, choosing an appropriate course of action typically hinges on the type of OOD data encountered. Unfortunately, the latter is generally not distinguished in practice, as modern OOD detection methods collapse distributional shifts into single scalar outlier scores. This work argues that scalar-based methods are thus insufficient for OOD data to be properly contextualized and prospectively exploited, a limitation we overcome with the introduction of DISC: Diffusion-based Statistical Characterization. DISC leverages the iterative denoising process of diffusion models to extract a rich, multi-dimensional feature vector that captures statistical discrepancies across multiple noise levels. Extensive experiments on image and tabular benchmarks show that DISC matches or surpasses state-of-the-art detectors for OOD detection and, crucially, also classifies OOD type, a capability largely absent from prior work. As such, our work enables a shift from simple binary OOD detection to a more granular detection.

Partial information decomposition (PID) of the multivariate mutual information describes the distinct ways in which a set of source variables contains information about a target variable. The groundbreaking work of Williams and Beer has shown that this decomposition cannot be determined from classic information theory without making additional assumptions, and several candidate measures have been proposed, often drawing on principles from related fields such as decision theory. None of these measures is differentiable with respect to the underlying probability mass function. We here present a novel measure that satisfies this property, emerges solely from information-theoretic principles, and has the form of a local mutual information. We show how the measure can be understood from the perspective of exclusions of probability mass, a principle that is foundational to the original definition of the mutual information by Fano. Since our measure is well-defined for individual realizations of the random variables it lends itself for example to local learning in artificial neural networks. We also show that it has a meaningful M\"{o}bius inversion on a redundancy lattice and obeys a target chain rule. We give an operational interpretation of the measure based on the decisions that an agent should take if given only the shared information.

Following previous work of ours in spherical symmetry, we here propose a new parametric framework to describe the spacetime of axisymmetric black holes in generic metric theories of gravity. In this case, the metric components are functions of both the radial and the polar angular coordinates, forcing a double expansion to obtain a generic axisymmetric metric expression. In particular, we use a continued-fraction expansion in terms of a compactified radial coordinate to express the radial dependence, while we exploit a Taylor expansion in terms of the cosine of the polar angle for the polar dependence. These choices lead to a superior convergence in the radial direction and to an exact limit on the equatorial plane. As a validation of our approach, we build parametrized representations of Kerr, rotating dilaton, and Einstein-dilaton-Gauss-Bonnet black holes. The match is already very good at lowest order in the expansion and improves as new orders are added. We expect a similar behavior for any stationary and axisymmetric black-hole metric.

The role of spin degrees of freedom in the quark-gluon plasma (QGP) has attracted significant interest in recent years. Spin hydrodynamics extends conventional hydrodynamics by incorporating spin via the spin tensor. In the mean-field limit of the Nambu-Jona-Lasinio (NJL) model under rigid rotation, spin degrees of freedom manifest naturally as axial-vector, or spin, condensate. We investigate the interplay between chiral and spin condensates in this framework. While rotation typically suppresses the formation of a chiral condensate, the presence of a spin condensate may counteract this effect, enhancing the chiral condensate. Moreover, it can alter the nature of the chiral transition from second to first order.

A simple effective model for the intermediate-density regime is constructed from the high-density effective theory of quantum chromodynamics (QCD). In the effective model, under a renormalization-group (RG) scaling towards low momenta, the original QCD interactions lead to four-quark contact interactions for the relevant quark and hole modes around the Fermi surface. The contact interaction in the scalar channel can be traced back to zero-sound-type collinear quark scattering near the Fermi surface in an instanton background. The quark and hole states in opposite directions of a given Fermi velocity form the collective scalar bosonic mode $\sigma$. The magnitude of $\sigma$ is investigated via the non-perturbative Functional Renormalization Group (FRG) evolution of the effective average action from the ultraviolet (UV) to the infrared (IR). In the mean background-field approximation for $\sigma$, nontrivial minima ($\bar{\sigma} \neq 0$) are found in the IR limit of the effective average action. A nonvanishing $\bar{\sigma}$ corresponds to condensation of quark and hole states in opposite directions of a given Fermi velocity, in a thin shell-like structure in momentum space around the Fermi surface. This looks similar to the shell-like baryon distribution in momentum space assumed in the quarkyonic-matter concept. However, when including a dynamic bosonic $\sigma$-mode in the RG flow, we find that its diffusive nature destroys the quark-hole condensate, i.e., the IR potential does not show any minima beyond the trivial one.

Despite the recent progress in deep learning, most approaches still go for a silo-like solution, focusing on learning each task in isolation: training a separate neural network for each individual task. Many real-world problems, however, call for a multi-modal approach and, therefore, for multi-tasking models. Multi-task learning (MTL) aims to leverage useful information across tasks to improve the generalization capability of a model. This thesis is concerned with multi-task learning in the context of computer vision. First, we review existing approaches for MTL. Next, we propose several methods that tackle important aspects of multi-task learning. The proposed methods are evaluated on various benchmarks. The results show several advances in the state-of-the-art of multi-task learning. Finally, we discuss several possibilities for future work.

Strongly supercooled first-order phase transitions have been proposed as a primordial black hole (PBH) production mechanism. While previous works rely on simplified models with limited thermodynamic precision, we stress that reliable theoretical PBH predictions require precise nucleation dynamics within realistic, classically conformal extensions of the Standard Model. By employing high-temperature dimensional reduction and computing the one-loop fluctuation determinants, we provide a state-of-the-art thermodynamic analysis and estimate the corresponding PBH abundance for classically conformal gauge-Higgs theories. Accounting for constraints from successful percolation and QCD chiral symmetry breaking, the parameter space where PBHs are viable dark matter candidates is severely limited.

A generalization of the determinant appears in particle physics in effective Lagrangian interaction terms that model the chiral anomaly in Quantum Chromodynamics (PRD 97 (2018) 9, 091901 PRD 109 (2024) 7, L071502), in particular in connection to mesons. This \textit{polydeterminant function}, known in the mathematical literature as a mixed discriminant, associates $N$ distinct $N\times N$ complex matrices into a complex number and reduces to the usual determinant when all matrices are taken as equal. Here, we explore the main properties of the polydeterminant applied to (quantum) fields by using a formalism and a language close to high-energy physics approaches. We discuss its use as a tool to write down novel chiral anomalous Lagrangian terms and present an explicit illustrative model for mesons. Finally, the extension of the polydeterminant as a function of tensors is shown.

We investigate the emergence of a resonant behavior in axion-trapped misalignment models featuring finite-temperature potential barriers. As the temperature decreases and the field is released from its trapped configuration, inhomogeneities are exponentially amplified through an instability in their equation of motion, leading to the fragmentation of the axion field. We show that this process constitutes a novel source of gravitational waves (GWs), analogous to those generated in zero-temperature axion fragmentation, but with distinct characteristics. We quantify the resulting GW spectrum, identifying the peak frequency and amplitude associated with the inhomogeneous axion dynamics. Our results indicate that the GW signal can be enhanced by up to two orders of magnitude compared to the standard fragmentation scenario, while exhibiting a markedly different spectral shape. The parameter space featuring both strong GW signals and reproducing the correct dark matter abundance is, however, limited.

In contrast to human vision, artificial neural networks (ANNs) remain relatively susceptible to adversarial attacks. To address this vulnerability, efforts have been made to transfer inductive bias from human brains to ANNs, often by training the ANN representations to match their biological counterparts. Previous works relied on brain data acquired in rodents or primates using invasive techniques, from specific regions of the brain, under non-natural conditions (anesthetized animals), and with stimulus datasets lacking diversity and naturalness. In this work, we explored whether aligning model representations to human EEG responses to a rich set of real-world images increases robustness to ANNs. Specifically, we trained ResNet50-backbone models on a dual task of classification and EEG prediction; and evaluated their EEG prediction accuracy and robustness to adversarial attacks. We observed significant correlation between the networks' EEG prediction accuracy, often highest around 100 ms post stimulus onset, and their gains in adversarial robustness. Although effect size was limited, effects were consistent across different random initializations and robust for architectural variants. We further teased apart the data from individual EEG channels and observed strongest contribution from electrodes in the parieto-occipital regions. The demonstrated utility of human EEG for such tasks opens up avenues for future efforts that scale to larger datasets under diverse stimuli conditions with the promise of stronger effects.

Purpose: Federated training is often hindered by heterogeneous datasets due to divergent data storage options, inconsistent naming schemes, varied annotation procedures, and disparities in label quality. This is particularly evident in the emerging multi-modal learning paradigms, where dataset harmonization including a uniform data representation and filtering options are of paramount importance. Methods: DICOM structured reports enable the standardized linkage of arbitrary information beyond the imaging domain and can be used within Python deep learning pipelines with highdicom. Building on this, we developed an open platform for data integration and interactive filtering capabilities that simplifies the process of assembling multi-modal datasets. Results: In this study, we extend our prior work by showing its applicability to more and divergent data types, as well as streamlining datasets for federated training within an established consortium of eight university hospitals in Germany. We prove its concurrent filtering ability by creating harmonized multi-modal datasets across all locations for predicting the outcome after minimally invasive heart valve replacement. The data includes DICOM data (i.e. computed tomography images, electrocardiography scans) as well as annotations (i.e. calcification segmentations, pointsets and pacemaker dependency), and metadata (i.e. prosthesis and diagnoses). Conclusion: Structured reports bridge the traditional gap between imaging systems and information systems. Utilizing the inherent DICOM reference system arbitrary data types can be queried concurrently to create meaningful cohorts for clinical studies. The graphical interface as well as example structured report templates will be made publicly available.

Continual learning in computer vision requires that models adapt to a continuous stream of tasks without forgetting prior knowledge, yet existing approaches often tip the balance heavily toward either plasticity or stability. We introduce RDBP, a simple, low-overhead baseline that unites two complementary mechanisms: ReLUDown, a lightweight activation modification that preserves feature sensitivity while preventing neuron dormancy, and Decreasing Backpropagation, a biologically inspired gradient-scheduling scheme that progressively shields early layers from catastrophic updates. Evaluated on the Continual ImageNet benchmark, RDBP matches or exceeds the plasticity and stability of state-of-the-art methods while reducing computational cost. RDBP thus provides both a practical solution for real-world continual learning and a clear benchmark against which future continual learning strategies can be measured.

We discuss the concept of Pure State of the Replica Symmetry Breaking ansatz in finite and infinite spin systems without averaging on the disorder, nor using replicas. Consider a system of n spins $\sigma\in\Omega^{n}$ with the usual set $\Omega=\left\{ -1,1\right\}$ of inner states and let $G:\,\Omega^{n}\rightarrow\left[0,1\right]$ a Gibbs measure on it of Hamiltonian $\mathcal{H}$ (also non random). We interpret the pure states of a model $\left(\Omega^{n},\mu\right)$ as disjoint subsets $\Omega^{n}$ such that the conditional measures behaves like product measures as in usual mean field approximations. Starting from such definition we try to reinterpret the RSB scheme and define an approximated probability measure. We then apply our results to the Sherrington-Kirkpatrick model to obtain the Parisi formula.

We extend the holographic V-QCD model by introducing a charged scalar field sector to represent the condensation of paired quark matter in the deconfined phase. By incorporating this new sector into the previously established framework for nuclear and quark matter, we obtain a phase diagram that, in addition to the first-order deconfinement transition and its critical end-point, also features a second-order transition between paired and unpaired quark matter. The critical temperature for quark pairing exhibits only a mild dependence on the chemical potential and can reach values as high as $T_\mathrm{crit} \approx 30~\rm MeV$. Comparison of the growth rate for the formation of homogeneous paired phases to the growth rate of previously discovered modulated phases suggests that the former is subdominant to the latter.

We employ the SMASH transport model to provide event-by-event initial conditions for the energy-momentum tensor and conserved charge currents in hydrodynamic simulations of relativistic heavy-ion collisions. We study the fluctuations and dynamical evolution of three conserved charge currents (net baryon, net electric charges, and net strangeness) with a 4D lattice-QCD-based equation of state, NEOS-4D, in the hydrodynamic phase. Out-of-equilibrium corrections at the particlization are generalized to finite densities to ensure the conservation of energy, momentum, and the three types of charges. These theoretical developments are integrated within X-SCAPE as a unified framework for studying the nuclear matter properties in the Beam Energy Scan program.