University of Wisconsin
Princeton Language and Intelligence introduces CharXiv, a new benchmark using diverse charts from arXiv with human-curated descriptive and reasoning questions, revealing a substantial gap between MLLM capabilities and human performance, with top models achieving less than 50% accuracy on reasoning tasks.
This paper presents χ²-Preference Optimization (χPO), a novel algorithm for offline language model alignment that addresses the problem of overoptimization. χPO replaces KL-regularization with a mixed χ²-divergence, providing provable robustness to overoptimization with single-policy concentrability guarantees, and empirically outperforms DPO by achieving higher winrates and greater stability on a summarization task.
Exploratory Preference Optimization (XPO) is presented as an online Reinforcement Learning from Human Feedback (RLHF) algorithm that enhances sample efficiency and active exploration in language models. It modifies Direct Preference Optimization (DPO) with an optimism-inspired bonus, enabling models to achieve strong performance on alignment benchmarks while requiring less preference data compared to passively exploratory baselines.
To address the dual challenges of inherent stochasticity and non-differentiable metrics in physical spatiotemporal forecasting, we propose Spatiotemporal Forecasting as Planning (SFP), a new paradigm grounded in Model-Based Reinforcement Learning. SFP constructs a novel Generative World Model to simulate diverse, high-fidelity future states, enabling an "imagination-based" environmental simulation. Within this framework, a base forecasting model acts as an agent, guided by a beam search-based planning algorithm that leverages non-differentiable domain metrics as reward signals to explore high-return future sequences. These identified high-reward candidates then serve as pseudo-labels to continuously optimize the agent's policy through iterative self-training, significantly reducing prediction error and demonstrating exceptional performance on critical domain metrics like capturing extreme events.
Camera image sensors can be used to detect ionizing radiation in addition to
optical photons. In particular, cosmic-ray muons are detected as long, straight
tracks passing through multiple pixels. The distribution of track lengths can
be related to the thickness of the active (depleted) region of the camera image
sensor through the known angular distribution of muons at sea level. We use a
sample of cosmic-ray muon tracks recorded by the Distributed Electronic
Cosmic-ray Observatory to measure the thickness of the depletion region of the
camera image sensor in a commercial smart phone, the HTC Wildfire S. The track
length distribution prefers a cosmic-ray muon angular distribution over an
isotropic distribution. Allowing either distribution, we measure the depletion
thickness to be between 13.9~μm and 27.7~μm. The same method can be
applied to additional models of image sensor. Once measured, the thickness can
be used to convert track length to incident polar angle on a per-event basis.
Combined with a determination of the incident azimuthal angle directly from the
track orientation in the sensor plane, this enables direction reconstruction of
individual cosmic-ray events.
30 Sep 2025
 University of Washington
University of Washington University of Illinois at Urbana-Champaign
University of Illinois at Urbana-Champaign University of Waterloo
University of Waterloo University of California, Santa Barbara
University of California, Santa Barbara Carnegie Mellon University
Carnegie Mellon University University of Notre Dame
University of Notre Dame University of Southern California
University of Southern California University of Chicago
University of Chicago National University of Singapore
National University of Singapore Stanford University
Stanford University Cornell UniversityOhio State University
Cornell UniversityOhio State University Texas A&M University
Texas A&M University University of GeorgiaIBM ResearchUniversity of WisconsinLehigh University
University of GeorgiaIBM ResearchUniversity of WisconsinLehigh University Allen Institute for AI
Allen Institute for AI Emory UniversityUniversity of Illinois Chicago
Emory UniversityUniversity of Illinois Chicago Arizona State University
Arizona State University University of MarylandMassachusetts General Hospital
University of MarylandMassachusetts General Hospital Mohamed bin Zayed University of Artificial IntelligenceSalesforce Research
Mohamed bin Zayed University of Artificial IntelligenceSalesforce Research Duke UniversitySingapore Management UniversityUniversity of QueenslandUniversity of MiamiCISPA – Helmholtz Center for Information SecurityUNC-Chapel Hill
Duke UniversitySingapore Management UniversityUniversity of QueenslandUniversity of MiamiCISPA – Helmholtz Center for Information SecurityUNC-Chapel HillA large consortium of 54 authors across 34 institutions established a unified set of eight guiding principles for trustworthy Generative Foundation Models (GenFMs). They introduced TrustGen, a dynamic benchmarking platform for continuous and comprehensive evaluation across seven trustworthiness dimensions for text-to-image, large language, and vision-language models, revealing overall progress while identifying persistent bottlenecks.
Scaling laws are a critical component of the LLM development pipeline, most famously as a way to forecast training decisions such as 'compute-optimally' trading-off parameter count and dataset size, alongside a more recent growing list of other crucial decisions. In this work, we ask whether compute-optimal scaling behaviour can be skill-dependent. In particular, we examine knowledge and reasoning-based skills such as knowledge-based QA and code generation, and we answer this question in the affirmative: scaling laws are skill-dependent. Next, to understand whether skill-dependent scaling is an artefact of the pretraining datamix, we conduct an extensive ablation of different datamixes and find that, also when correcting for datamix differences, knowledge and code exhibit fundamental differences in scaling behaviour. We conclude with an analysis of how our findings relate to standard compute-optimal scaling using a validation set, and find that a misspecified validation set can impact compute-optimal parameter count by nearly 50%, depending on its skill composition.
In sequential recommendation, models recommend items based on user's interaction history. To this end, current models usually incorporate information such as item descriptions and user intent or preferences. User preferences are usually not explicitly given in open-source datasets, and thus need to be approximated, for example via large language models (LLMs). Current approaches leverage approximated user preferences only during training and rely solely on the past interaction history for recommendations, limiting their ability to dynamically adapt to changing preferences, potentially reinforcing echo chambers. To address this issue, we propose a new paradigm, namely preference discerning, which explicitly conditions a generative recommendation model on user preferences in natural language within its context. To evaluate preference discerning, we introduce a novel benchmark that provides a holistic evaluation across various scenarios, including preference steering and sentiment following. Upon evaluating current state-of-the-art methods on our benchmark, we discover that their ability to dynamically adapt to evolving user preferences is limited. To address this, we propose a new method named Mender (Multimodal Preference Discerner), which achieves state-of-the-art performance in our benchmark. Our results show that Mender effectively adapts its recommendation guided by human preferences, even if not observed during training, paving the way toward more flexible recommendation models.
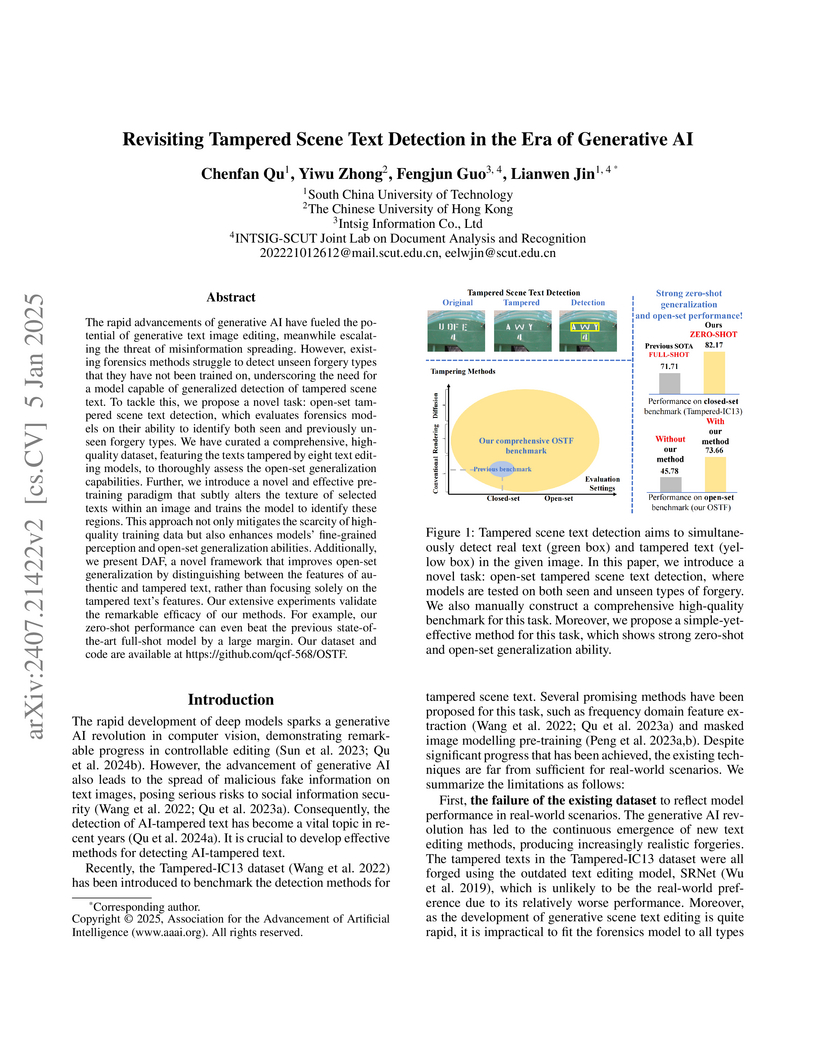
Researchers from South China University of Technology and IntSig Joint Lab developed a new benchmark dataset (OSTF) and proposed methods—Texture Jitter pre-training and Difference-Aware Forensics (DAF)—to improve the detection of AI-generated tampered scene text. Their approach achieved 10.5 mIoU points higher than prior state-of-the-art in zero-shot settings on the Tampered-IC13 dataset and demonstrated enhanced open-set generalization on the new OSTF dataset.
Summarization is one of the most common tasks performed by large language models (LLMs), especially in applications like Retrieval-Augmented Generation (RAG). However, existing evaluations of hallucinations in LLM-generated summaries, and evaluations of hallucination detection models both suffer from a lack of diversity and recency in the LLM and LLM families considered. This paper introduces FaithBench, a summarization hallucination benchmark comprising challenging hallucinations made by 10 modern LLMs from 8 different families, with ground truth annotations by human experts. ``Challenging'' here means summaries on which popular, state-of-the-art hallucination detection models, including GPT-4o-as-a-judge, disagreed on. Our results show GPT-4o and GPT-3.5-Turbo produce the least hallucinations. However, even the best hallucination detection models have near 50\% accuracies on FaithBench, indicating lots of room for future improvement. The repo is this https URL
University of FreiburgGerman Centre for Integrative Biodiversity Research (iDiv)Leipzig University McGill UniversityUniversity of WisconsinColorado State UniversitySimon Fraser UniversityMila - Québec AI InstituteCenter for Scalable Data Analytics and Artificial Intelligence (ScaDS.AI)University of SalfordHelmholtz Centre for Environmental Research
UFZ
McGill UniversityUniversity of WisconsinColorado State UniversitySimon Fraser UniversityMila - Québec AI InstituteCenter for Scalable Data Analytics and Artificial Intelligence (ScaDS.AI)University of SalfordHelmholtz Centre for Environmental Research
UFZ
 McGill UniversityUniversity of WisconsinColorado State UniversitySimon Fraser UniversityMila - Québec AI InstituteCenter for Scalable Data Analytics and Artificial Intelligence (ScaDS.AI)University of SalfordHelmholtz Centre for Environmental Research
UFZ
McGill UniversityUniversity of WisconsinColorado State UniversitySimon Fraser UniversityMila - Québec AI InstituteCenter for Scalable Data Analytics and Artificial Intelligence (ScaDS.AI)University of SalfordHelmholtz Centre for Environmental Research
UFZPlant traits such as leaf carbon content and leaf mass are essential variables in the study of biodiversity and climate change. However, conventional field sampling cannot feasibly cover trait variation at ecologically meaningful spatial scales. Machine learning represents a valuable solution for plant trait prediction across ecosystems, leveraging hyperspectral data from remote sensing. Nevertheless, trait prediction from hyperspectral data is challenged by label scarcity and substantial domain shifts (\eg across sensors, ecological distributions), requiring robust cross-domain methods. Here, we present GreenHyperSpectra, a pretraining dataset encompassing real-world cross-sensor and cross-ecosystem samples designed to benchmark trait prediction with semi- and self-supervised methods. We adopt an evaluation framework encompassing in-distribution and out-of-distribution scenarios. We successfully leverage GreenHyperSpectra to pretrain label-efficient multi-output regression models that outperform the state-of-the-art supervised baseline. Our empirical analyses demonstrate substantial improvements in learning spectral representations for trait prediction, establishing a comprehensive methodological framework to catalyze research at the intersection of representation learning and plant functional traits assessment. All code and data are available at: this https URL.
We review the state of the art in the detection of extreme high-energy neutrinos, focusing on the IceCube and KM3NeT neutrino telescopes. IceCube, operating deep in Antarctic ice, and KM3NeT, a new array in the Mediterranean Sea, employ distinct designs to capture Cherenkov light from neutrino interactions. We examine their detector architectures, readout and reconstruction performance for PeV-scale and higher-energy neutrinos. Recent candidate events above 5 PeV are highlighted. These include a ~120 PeV muon track observed by KM3NeT in 2023, and IceCube's highest-energy detections, which comprise several-PeV showers and tracks. We outline current approaches to neutrino energy reconstruction and explore scenarios that might explain the apparent differences in observed event characteristics. Finally, we summarize future prospects for extreme-energy neutrino observations and their implications for astrophysical source populations and cosmogenic neutrinos.
30 Aug 2025
As neuroscientific theories of consciousness continue to proliferate, the need to assess their similarities and differences -- as well as their predictive and explanatory power -- becomes ever more pressing. Recently, a number of structured adversarial collaborations have been devised to test the competing predictions of several candidate theories of consciousness. In this review, we compare and contrast three theories being investigated in one such adversarial collaboration: Integrated Information Theory, Neurorepresentationalism, and Active Inference. We begin by presenting the core claims of each theory, before comparing them in terms of (1) the phenomena they seek to explain, (2) the sorts of explanations they avail, and (3) the methodological strategies they endorse. We then consider some of the inherent challenges of theory testing, and how adversarial collaboration addresses some of these difficulties. More specifically, we outline the key hypotheses that will be tested in this adversarial collaboration, and exemplify how contrasting empirical predictions may pertain to core and auxiliary components of each theory. Finally, we discuss how the data harvested across disparate experiments (and their replicates) may be formally integrated to provide a quantitative measure of the evidential support accrued under each theory. We suggest this approach to theory comparison may afford a useful metric for tracking the amount of scientific progress being made in consciousness research.
 University of Illinois at Urbana-Champaign
University of Illinois at Urbana-Champaign Carnegie Mellon University
Carnegie Mellon University University of Southern California
University of Southern California University of OxfordIndiana University
University of OxfordIndiana University Stanford University
Stanford University University of Copenhagen
University of Copenhagen MetaUniversity of Wisconsin
MetaUniversity of Wisconsin University of Maryland
University of Maryland Mohamed bin Zayed University of Artificial IntelligenceKorea Advanced Institute of Science and TechnologyIndian Institute of Technology DelhiFull FactNewtralesPagella Politica/Facta
Mohamed bin Zayed University of Artificial IntelligenceKorea Advanced Institute of Science and TechnologyIndian Institute of Technology DelhiFull FactNewtralesPagella Politica/FactaA comprehensive, multidisciplinary analysis identifies the multifaceted risks to information veracity posed by Large Language Models, detailing both their inherent factual limitations and potential for malicious exploitation. The analysis concludes with a multi-pronged agenda encompassing technological, regulatory, and educational interventions to mitigate these threats and ensure responsible AI development.
Existing Image Manipulation Localization (IML) methods mostly rely heavily on
task-specific designs, making them perform well only on the target IML task,
while joint training on multiple IML tasks causes significant performance
degradation, hindering real applications.
To this end, we propose Omni-IML, the first generalist model designed to
unify IML across diverse tasks.
Specifically, Omni-IML achieves generalization through three key components:
(1) a Modal Gate Encoder, which adaptively selects the optimal encoding
modality per sample, (2) a Dynamic Weight Decoder, which dynamically adjusts
decoder filters to the task at hand, and (3) an Anomaly Enhancement module that
leverages box supervision to highlight the tampered regions and facilitate the
learning of task-agnostic features.
Beyond localization, to support interpretation of the tampered images, we
construct Omni-273k, a large high-quality dataset that includes natural
language descriptions of tampered artifact. It is annotated through our
automatic, chain-of-thoughts annotation technique.
We also design a simple-yet-effective interpretation module to better utilize
these descriptive annotations.
Our extensive experiments show that our single Omni-IML model achieves
state-of-the-art performance across all four major IML tasks, providing a
valuable solution for practical deployment and a promising direction of
generalist models in image forensics. Our code and dataset will be publicly
available.
02 Dec 2025
Thermal freeze-out is a compelling framework for naturally generating the dark matter abundance. We systematically study a broad range of dark matter and mediator particle combinations that can viably realize thermal freeze-out, focusing on models in which the mediator couples to Standard Model quarks. In each case, we calculate the relic density and consider existing constraints from accelerators, cosmology, direct detection, and indirect detection over the full range of dark matter and mediator masses. We present an encyclopedic catalog of matrix elements, cross sections, and decay rates which can be used as a reference for future studies of dark matter phenomenology.
The meaningful use of electronic health records (EHR) continues to progress in the digital era with clinical decision support systems augmented by artificial intelligence. A priority in improving provider experience is to overcome information overload and reduce the cognitive burden so fewer medical errors and cognitive biases are introduced during patient care. One major type of medical error is diagnostic error due to systematic or predictable errors in judgment that rely on heuristics. The potential for clinical natural language processing (cNLP) to model diagnostic reasoning in humans with forward reasoning from data to diagnosis and potentially reduce the cognitive burden and medical error has not been investigated. Existing tasks to advance the science in cNLP have largely focused on information extraction and named entity recognition through classification tasks. We introduce a novel suite of tasks coined as Diagnostic Reasoning Benchmarks, DR.BENCH, as a new benchmark for developing and evaluating cNLP models with clinical diagnostic reasoning ability. The suite includes six tasks from ten publicly available datasets addressing clinical text understanding, medical knowledge reasoning, and diagnosis generation. DR.BENCH is the first clinical suite of tasks designed to be a natural language generation framework to evaluate pre-trained language models. Experiments with state-of-the-art pre-trained generative language models using large general domain models and models that were continually trained on a medical corpus demonstrate opportunities for improvement when evaluated in DR. BENCH. We share DR. BENCH as a publicly available GitLab repository with a systematic approach to load and evaluate models for the cNLP community.
This paper examines the problem of ranking a collection of objects using
pairwise comparisons (rankings of two objects). In general, the ranking of n
objects can be identified by standard sorting methods using nlog2n
pairwise comparisons. We are interested in natural situations in which
relationships among the objects may allow for ranking using far fewer pairwise
comparisons. Specifically, we assume that the objects can be embedded into a
d-dimensional Euclidean space and that the rankings reflect their relative
distances from a common reference point in Rd. We show that under this
assumption the number of possible rankings grows like n2d and demonstrate
an algorithm that can identify a randomly selected ranking using just slightly
more than dlogn adaptively selected pairwise comparisons, on average. If
instead the comparisons are chosen at random, then almost all pairwise
comparisons must be made in order to identify any ranking. In addition, we
propose a robust, error-tolerant algorithm that only requires that the pairwise
comparisons are probably correct. Experimental studies with synthetic and real
datasets support the conclusions of our theoretical analysis.
08 Jul 2025
We study a class of convex-concave min-max problems in which the coupled component of the objective is linear in at least one of the two decision vectors. We identify such problem structure as interpolating between the bilinearly and nonbilinearly coupled problems, motivated by key applications in areas such as distributionally robust optimization and convex optimization with functional constraints. Leveraging the considered nonlinear-linear coupling of the primal and the dual decision vectors, we develop a general algorithmic framework leading to fine-grained complexity bounds exploiting separability properties of the problem, whenever present. The obtained complexity bounds offer potential improvements over state-of-the-art scaling with n or n in some of the considered problem settings, which even include bilinearly coupled problems, where n is the dimension of the dual decision vector. On the algorithmic front, our work provides novel strategies for combining randomization with extrapolation and multi-point anchoring in the mirror descent-style updates in the primal and the dual, which we hope will find further applications in addressing related optimization problems. %
30 Dec 2022
Integrated Information Theory (IIT) 4.0 presents a refined and expanded mathematical framework that objectively defines and quantifies subjective experience, translating phenomenal properties into physical cause-effect structures.
There are no more papers matching your filters at the moment.