We consider the problem of sampling distributions stemming from non-convex potentials with Unadjusted Langevin Algorithm (ULA). We prove the stability of the discrete-time ULA to drift approximations under the assumption that the potential is strongly convex at infinity. In many context, e.g. imaging inverse problems, potentials are non-convex and non-smooth. Proximal Stochastic Gradient Langevin Algorithm (PSGLA) is a popular algorithm to handle such potentials. It combines the forward-backward optimization algorithm with a ULA step. Our main stability result combined with properties of the Moreau envelope allows us to derive the first proof of convergence of the PSGLA for non-convex potentials. We empirically validate our methodology on synthetic data and in the context of imaging inverse problems. In particular, we observe that PSGLA exhibits faster convergence rates than Stochastic Gradient Langevin Algorithm for posterior sampling while preserving its restoration properties.

In this document, we present the main properties satisfied by the Moreau envelope of weakly convex functions. The Moreau envelope has been introduced in convex optimization to regularize convex functionals while preserving their global minimizers. However, the Moreau envelope is also defined for the more general class of weakly convex function and can be a useful tool for optimization in this context. The main properties of the Moreau envelope have been demonstrated for convex functions and are generalized to weakly convex function in various works. This document summarizes the vast literature on the properties of the Moreau envelope and provides the associated proofs.

We revisit the monotonicity of relative entropy under the action of quantum channels, a foundational result in quantum information theory. Among the several available proofs, we focus on those by Petz and Uhlmann, which we reformulate within a unified, finite-dimensional operator-theoretic framework. In the first part, we examine Petz's strategy, identify a subtle flaw in his original use of Jensen's contractive operator inequality, and point out how it was corrected to restore the validity of his line of reasoning. In the second part, we develop Uhlmann's approach, which is based on interpolations of positive sesquilinear forms and applies automatically also to non-invertible density operators. By comparing these two approaches, we highlight their complementary strengths: Petz's method is more direct and clear, Uhlmann's is more abstract and general. Our treatment aims to clarify the mathematical structure underlying the monotonicity of relative entropy and to make these proofs more accessible to a broader audience interested in both the foundations and the applications of quantum information theory.

The Feinberg-Piunovskiy Theorem established in [14, Theorem 3.8] asserts that for a discrete-time uniformly absorbing and atomless Markov Decision Process (MDP) with Borel state space and multiple criteria, the family of deterministic stationary policies is a sufficient class of policies. In this paper, we study some related problems and some extensions. In particular dropping the atomless hypothesis, we establish that the set of chattering stationary policies is a sufficient class of policies for uniformly absorbing MDPs with measurable state space and multiple criteria. We also prove the Feinberg-Piunovskiy Theorem in the context of a measurable state space in two different ways that differ from \cite{piunovskiy19}. In particular, we show that the sufficiency of chattering stationary policies directly yields the sufficiency of deterministics stationary policies for atomless models. Our approach is partially based on the analysis of extreme points of certain convex sets of occupation measures satisfying integral type constraints. We show that for a uniformly absorbing model an extreme point of such sets is necessarily given by occupation measures induced by chattering stationary policies of order $d+1$ where $d$ is the dimension of the vector of constraints. When in addition the model $\mathsf{M}$ is atomless, then the extreme points of this constrained set of occupation measures are precisely the occupation measures generated by deterministic stationary policies satisfying these constraints.

Superpixels are widely used in computer vision to simplify image representation and reduce computational complexity. While traditional methods rely on low-level features, deep learning-based approaches leverage high-level features but also tend to sacrifice regularity of superpixels to capture complex objects, leading to accurate but less interpretable segmentations. In this work, we introduce SPAM (SuperPixel Anything Model), a versatile framework for segmenting images into accurate yet regular superpixels. We train a model to extract image features for superpixel generation, and at inference, we leverage a large-scale pretrained model for semantic-agnostic segmentation to ensure that superpixels align with object masks. SPAM can handle any prior high-level segmentation, resolving uncertainty regions, and is able to interactively focus on specific objects. Comprehensive experiments demonstrate that SPAM qualitatively and quantitatively outperforms state-of-the-art methods on segmentation tasks, making it a valuable and robust tool for various applications. Code and pre-trained models are available here: this https URL.

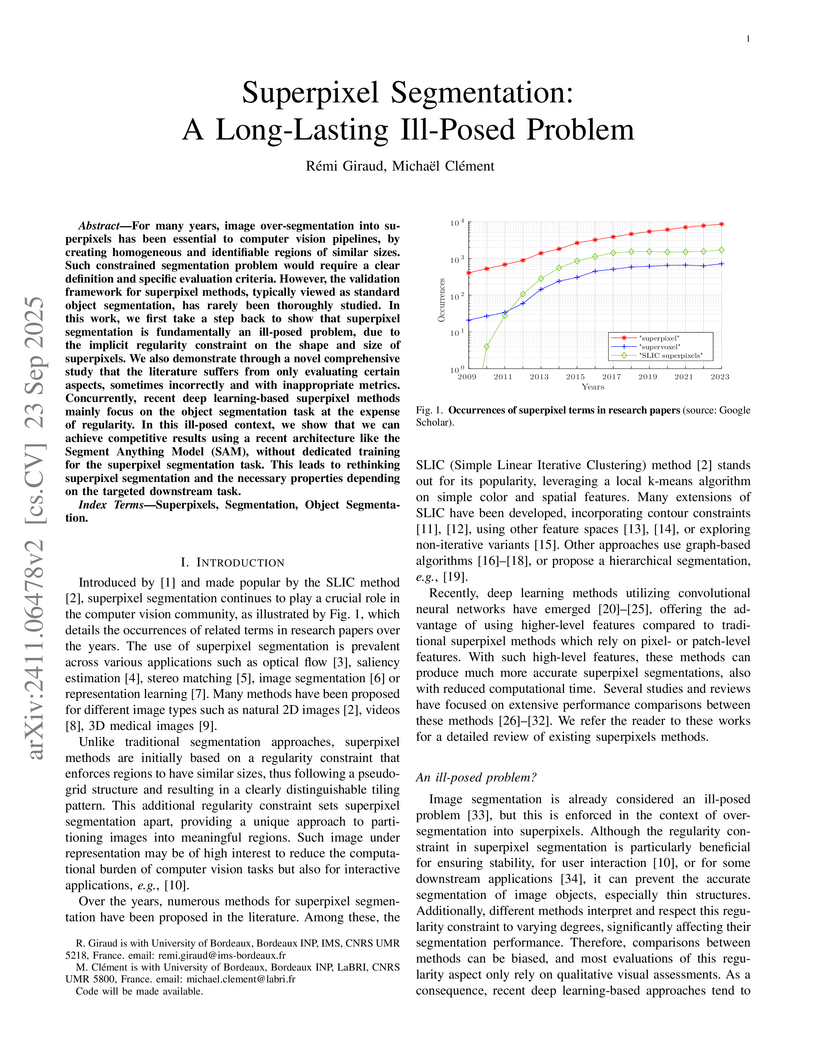
For many years, image over-segmentation into superpixels has been essential to computer vision pipelines, by creating homogeneous and identifiable regions of similar sizes. Such constrained segmentation problem would require a clear definition and specific evaluation criteria. However, the validation framework for superpixel methods, typically viewed as standard object segmentation, has rarely been thoroughly studied. In this work, we first take a step back to show that superpixel segmentation is fundamentally an ill-posed problem, due to the implicit regularity constraint on the shape and size of superpixels. We also demonstrate through a novel comprehensive study that the literature suffers from only evaluating certain aspects, sometimes incorrectly and with inappropriate metrics. Concurrently, recent deep learning-based superpixel methods mainly focus on the object segmentation task at the expense of regularity. In this ill-posed context, we show that we can achieve competitive results using a recent architecture like the Segment Anything Model (SAM), without dedicated training for the superpixel segmentation task. This leads to rethinking superpixel segmentation and the necessary properties depending on the targeted downstream task.

Plug-and-Play methods constitute a class of iterative algorithms for imaging problems where regularization is performed by an off-the-shelf denoiser. Although Plug-and-Play methods can lead to tremendous visual performance for various image problems, the few existing convergence guarantees are based on unrealistic (or suboptimal) hypotheses on the denoiser, or limited to strongly convex data terms. In this work, we propose a new type of Plug-and-Play methods, based on half-quadratic splitting, for which the denoiser is realized as a gradient descent step on a functional parameterized by a deep neural network. Exploiting convergence results for proximal gradient descent algorithms in the non-convex setting, we show that the proposed Plug-and-Play algorithm is a convergent iterative scheme that targets stationary points of an explicit global functional. Besides, experiments show that it is possible to learn such a deep denoiser while not compromising the performance in comparison to other state-of-the-art deep denoisers used in Plug-and-Play schemes. We apply our proximal gradient algorithm to various ill-posed inverse problems, e.g. deblurring, super-resolution and inpainting. For all these applications, numerical results empirically confirm the convergence results. Experiments also show that this new algorithm reaches state-of-the-art performance, both quantitatively and qualitatively.

Machine learning and deep learning models have become essential in the recent fast development of artificial intelligence in many sectors of the society. It is now widely acknowledge that the development of these models has an environmental cost that has been analyzed in many studies. Several online and software tools have been developed to track energy consumption while training machine learning models. In this paper, we propose a comprehensive introduction and comparison of these tools for AI practitioners wishing to start estimating the environmental impact of their work. We review the specific vocabulary, the technical requirements for each tool. We compare the energy consumption estimated by each tool on two deep neural networks for image processing and on different types of servers. From these experiments, we provide some advice for better choosing the right tool and infrastructure.

We present a discretization-free scalable framework for solving a large class of mass-conserving partial differential equations (PDEs), including the time-dependent Fokker-Planck equation and the Wasserstein gradient flow. The main observation is that the time-varying velocity field of the PDE solution needs to be self-consistent: it must satisfy a fixed-point equation involving the probability flow characterized by the same velocity field. Instead of directly minimizing the residual of the fixed-point equation with neural parameterization, we use an iterative formulation with a biased gradient estimator that bypasses significant computational obstacles with strong empirical performance. Compared to existing approaches, our method does not suffer from temporal or spatial discretization, covers a wider range of PDEs, and scales to high dimensions. Experimentally, our method recovers analytical solutions accurately when they are available and achieves superior performance in high dimensions with less training time compared to alternatives.

Dynamic networks are a complex subject. Not only do they inherit the complexity of static networks (as a particular case); they are also sensitive to definitional subtleties that are a frequent source of confusion and incomparability of results in the literature. In this paper, we take a step back and examine three such aspects in more details, exploring their impact in a systematic way; namely, whether the temporal paths are required to be \emph{strict} (i.e., the times along a path must increasing, not just be non-decreasing), whether the time labeling is \emph{proper} (two adjacent edges cannot be present at the same time) and whether the time labeling is \emph{simple} (an edge can have only one presence time). In particular, we investigate how different combinations of these features impact the expressivity of the graph in terms of reachability. Our results imply a hierarchy of expressivity for the resulting settings, shedding light on the loss of generality that one is making when considering either combination. Some settings are more general than expected; in particular, proper temporal graphs turn out to be as expressive as general temporal graphs where non-strict paths are allowed. Also, we show that the simplest setting, that of \emph{happy} temporal graphs (i.e., both proper and simple) remains expressive enough to emulate the reachability of general temporal graphs in a certain (restricted but useful) sense. Furthermore, this setting is advocated as a target of choice for proving negative results. We illustrates this by strengthening two known results to happy graphs (namely, the inexistence of sparse spanners, and the hardness of computing temporal components). Overall, we hope that this article can be seen as a guide for choosing between different settings of temporal graphs, while being aware of the way these choices affect generality.

The growing integration of Artificial Intelligence (AI) into education has intensified the need for transparency and interpretability. While hackathons have long served as agile environments for rapid AI prototyping, few have directly addressed eXplainable AI (XAI) in real-world educational contexts. This paper presents a comprehensive analysis of the XAI Challenge 2025, a hackathon-style competition jointly organized by Ho Chi Minh City University of Technology (HCMUT) and the International Workshop on Trustworthiness and Reliability in Neurosymbolic AI (TRNS-AI), held as part of the International Joint Conference on Neural Networks (IJCNN 2025). The challenge tasked participants with building Question-Answering (QA) systems capable of answering student queries about university policies while generating clear, logic-based natural language explanations. To promote transparency and trustworthiness, solutions were required to use lightweight Large Language Models (LLMs) or hybrid LLM-symbolic systems. A high-quality dataset was provided, constructed via logic-based templates with Z3 validation and refined through expert student review to ensure alignment with real-world academic scenarios. We describe the challenge's motivation, structure, dataset construction, and evaluation protocol. Situating the competition within the broader evolution of AI hackathons, we argue that it represents a novel effort to bridge LLMs and symbolic reasoning in service of explainability. Our findings offer actionable insights for future XAI-centered educational systems and competitive research initiatives.

We propose a physics-informed machine learning framework called P-DivGNN to reconstruct local stress fields at the micro-scale, in the context of multi-scale simulation given a periodic micro-structure mesh and mean, macro-scale, stress values. This method is based in representing a periodic micro-structure as a graph, combined with a message passing graph neural network. We are able to retrieve local stress field distributions, providing average stress values produced by a mean field reduced order model (ROM) or Finite Element (FE) simulation at the macro-scale. The prediction of local stress fields are of utmost importance considering fracture analysis or the definition of local fatigue criteria. Our model incorporates physical constraints during training to constraint local stress field equilibrium state and employs a periodic graph representation to enforce periodic boundary conditions. The benefits of the proposed physics-informed GNN are evaluated considering linear and non linear hyperelastic responses applied to varying geometries. In the non-linear hyperelastic case, the proposed method achieves significant computational speed-ups compared to FE simulation, making it particularly attractive for large-scale applications.

Most superpixel algorithms compute a trade-off between spatial and color features at the pixel level. Hence, they may need fine parameter tuning to balance the two measures, and highly fail to group pixels with similar local texture properties. In this paper, we address these issues with a new Texture-Aware SuperPixel (TASP) method. To accurately segment textured and smooth areas, TASP automatically adjusts its spatial constraint according to the local feature variance. Then, to ensure texture homogeneity within superpixels, a new pixel to superpixel patch-based distance is proposed. TASP outperforms the segmentation accuracy of the state-of-the-art methods on texture and also natural color image datasets.

Dense image matching aims to find a correspondent for every pixel of a source image in a partially overlapping target image. State-of-the-art methods typically rely on a coarse-to-fine mechanism where a single correspondent hypothesis is produced per source location at each scale. In challenging cases -- such as at depth discontinuities or when the target image is a strong zoom-in of the source image -- the correspondents of neighboring source locations are often widely spread and predicting a single correspondent hypothesis per source location at each scale may lead to erroneous matches. In this paper, we investigate the idea of predicting multiple correspondent hypotheses per source location at each scale instead. We consider a beam search strategy to propagat multiple hypotheses at each scale and propose integrating these multiple hypotheses into cross-attention layers, resulting in a novel dense matching architecture called BEAMER. BEAMER learns to preserve and propagate multiple hypotheses across scales, making it significantly more robust than state-of-the-art methods, especially at depth discontinuities or when the target image is a strong zoom-in of the source image.

Over the years, the use of superpixel segmentation has become very popular in various applications, serving as a preprocessing step to reduce data size by adapting to the content of the image, regardless of its semantic content. While the superpixel segmentation of standard planar images, captured with a 90° field of view, has been extensively studied, there has been limited focus on dedicated methods to omnidirectional or spherical images, captured with a 360° field of view. In this study, we introduce the first deep learning-based superpixel segmentation approach tailored for omnidirectional images called DSS (for Deep Spherical Superpixels). Our methodology leverages on spherical CNN architectures and the differentiable K-means clustering paradigm for superpixels, to generate superpixels that follow the spherical geometry. Additionally, we propose to use data augmentation techniques specifically designed for 360° images, enabling our model to efficiently learn from a limited set of annotated omnidirectional data. Our extensive validation across two datasets demonstrates that taking into account the inherent circular geometry of such images into our framework improves the segmentation performance over traditional and deep learning-based superpixel methods. Our code is available online.

Empirically, it has been observed that adding momentum to Stochastic Gradient Descent (SGD) accelerates the convergence of the algorithm. However, the literature has been rather pessimistic, even in the case of convex functions, about the possibility of theoretically proving this observation. We investigate the possibility of obtaining accelerated convergence of the Stochastic Nesterov Accelerated Gradient (SNAG), a momentum-based version of SGD, when minimizing a sum of functions in a convex setting. We demonstrate that the average correlation between gradients allows to verify the strong growth condition, which is the key ingredient to obtain acceleration with SNAG. Numerical experiments, both in linear regression and deep neural network optimization, confirm in practice our theoretical results.

Superpixel decomposition methods are generally used as a pre-processing step to speed up image processing tasks. They group the pixels of an image into homogeneous regions while trying to respect existing contours. For all state-of-the-art superpixel decomposition methods, a trade-off is made between 1) computational time, 2) adherence to image contours and 3) regularity and compactness of the decomposition. In this paper, we propose a fast method to compute Superpixels with Contour Adherence using Linear Path (SCALP) in an iterative clustering framework. The distance computed when trying to associate a pixel to a superpixel during the clustering is enhanced by considering the linear path to the superpixel barycenter. The proposed framework produces regular and compact superpixels that adhere to the image contours. We provide a detailed evaluation of SCALP on the standard Berkeley Segmentation Dataset. The obtained results outperform state-of-the-art methods in terms of standard superpixel and contour detection metrics.

The aim of the review is to consolidate the core aspects of the Stroh formalism, trace the development of the impedance matrix concept, and outline the range of acoustic problems that have been treated by these methods over the last two and a half decades.

Physical colors, i.e. reflected or emitted lights entering the eyes from a visual environment, are converted into perceived colors sensed by humans by neurophysiological mechanisms. These processes involve both three types of photoreceptors, the LMS cones, and spectrally opponent and non-opponent interactions resulting from the activity rates of ganglion and lateral geniculate nucleus cells. Thus, color perception is a phenomenon inherently linked to an experimental environment (the visual scene) and an observing apparatus (the human visual system). This is clearly reminiscent of the conceptual foundation of both relativity and quantum mechanics, where the link is between a physical system and the measuring instruments. The relationship between color perception and relativity was explicitly examined for the first time by the physicist H. Yilmaz in 1962 from an experimental point of view. The main purpose of this contribution is to present a rigorous mathematical model that, by taking into account both trichromacy and color opponency, permits to explain on a purely theoretical basis the relativistic color perception phenomena argued by Yilmaz. Instead of relying directly on relativistic considerations, we base our theory on a quantum interpretation of color perception together with just one assumption, called trichromacy axiom, that summarizes well-established properties of trichromatic color vision within the framework of Jordan algebras. We show how this approach allows us to reconcile trichromacy with Hering's opponency and also to derive the relativistic properties of perceived colors without any additional mathematical or experimental assumption.

We investigate the problem of producing diverse solutions to an image super-resolution problem. From a probabilistic perspective, this can be done by sampling from the posterior distribution of an inverse problem, which requires the definition of a prior distribution on the high-resolution images. In this work, we propose to use a pretrained hierarchical variational autoencoder (HVAE) as a prior. We train a lightweight stochastic encoder to encode low-resolution images in the latent space of a pretrained HVAE. At inference, we combine the low-resolution encoder and the pretrained generative model to super-resolve an image. We demonstrate on the task of face super-resolution that our method provides an advantageous trade-off between the computational efficiency of conditional normalizing flows techniques and the sample quality of diffusion based methods.