Criteo AI LAB
University of Oslo University of California, Santa Barbara
University of California, Santa Barbara New York University
New York University National University of Singapore
National University of Singapore University of Science and Technology of China
University of Science and Technology of China Tsinghua UniversityUniversity of Electronic Science and Technology of ChinaOhio State University
Tsinghua UniversityUniversity of Electronic Science and Technology of ChinaOhio State University Peking University
Peking University University of British Columbia
University of British Columbia Yale University
Yale University Purdue University
Purdue University University of California, Santa CruzUniversity of BarcelonaKuaishou Technology Co., Ltd.EleutherAIWroclaw University of Science and TechnologyCriteo AI LABRWKV FoundationRuoxinTechZendeskEPITACharm TherapeuticsNextremer Co. Ltd.Databaker Technology Co. LtdCrisis24Storyteller.io
University of California, Santa CruzUniversity of BarcelonaKuaishou Technology Co., Ltd.EleutherAIWroclaw University of Science and TechnologyCriteo AI LABRWKV FoundationRuoxinTechZendeskEPITACharm TherapeuticsNextremer Co. Ltd.Databaker Technology Co. LtdCrisis24Storyteller.io
 University of California, Santa Barbara
University of California, Santa Barbara New York University
New York University National University of Singapore
National University of Singapore University of Science and Technology of China
University of Science and Technology of China Tsinghua UniversityUniversity of Electronic Science and Technology of ChinaOhio State University
Tsinghua UniversityUniversity of Electronic Science and Technology of ChinaOhio State University Peking University
Peking University University of British Columbia
University of British Columbia Yale University
Yale University Purdue University
Purdue University University of California, Santa CruzUniversity of BarcelonaKuaishou Technology Co., Ltd.EleutherAIWroclaw University of Science and TechnologyCriteo AI LABRWKV FoundationRuoxinTechZendeskEPITACharm TherapeuticsNextremer Co. Ltd.Databaker Technology Co. LtdCrisis24Storyteller.io
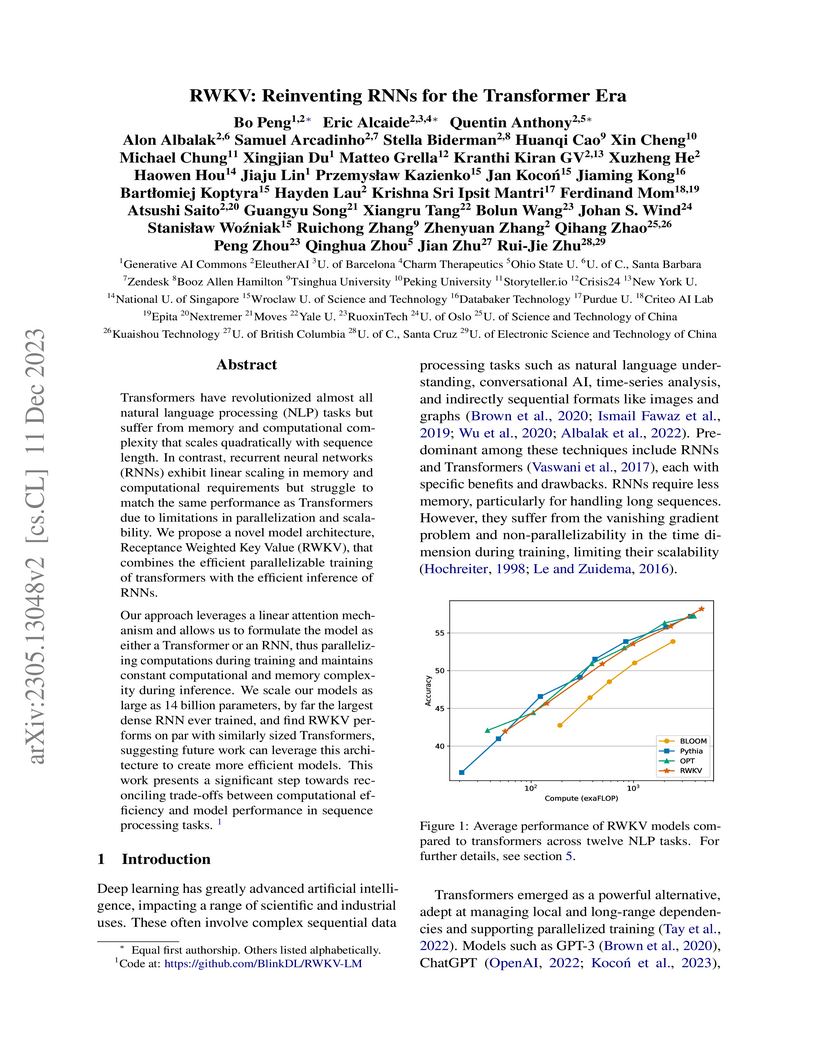
University of California, Santa CruzUniversity of BarcelonaKuaishou Technology Co., Ltd.EleutherAIWroclaw University of Science and TechnologyCriteo AI LABRWKV FoundationRuoxinTechZendeskEPITACharm TherapeuticsNextremer Co. Ltd.Databaker Technology Co. LtdCrisis24Storyteller.ioResearchers at EleutherAI, with support from StabilityAI, developed RWKV, a novel deep learning architecture that functions as a Transformer for parallel training and an RNN for efficient inference. RWKV models, scaled up to 14 billion parameters, achieve performance comparable to similarly sized Transformers across various NLP benchmarks while offering linear scaling in memory and computation during inference, making them efficient for long sequences and deployment on constrained hardware.
The behavior of Large Language Models (LLMs) when facing contextual information that conflicts with their internal parametric knowledge is inconsistent, with no generally accepted explanation for the expected outcome distribution. Recent work has identified in autoregressive transformer models a class of neurons -- called entropy neurons -- that produce a significant effect on the model output entropy while having an overall moderate impact on the ranking of the predicted tokens. In this paper, we investigate the preliminary claim that these neurons are involved in inhibiting context copying behavior in transformers by looking at their role in resolving conflicts between contextual and parametric information. We show that entropy neurons are responsible for suppressing context copying across a range of LLMs, and that ablating them leads to a significant change in the generation process. These results enhance our understanding of the internal dynamics of LLMs when handling conflicting information.
Researchers from Sorbonne Université and Criteo AI Lab introduce ECHO, a framework for efficient generative transformer operators that addresses the scalability and long-horizon error accumulation issues in neural operators for PDEs. ECHO achieves high spatio-temporal compression and accurate, multi-task solutions for million-point PDE trajectories, notably enabling super-resolution forecasting on a 1024x1024 Vorticity grid without out-of-memory errors where other models failed.
Recent work has explored generative recommender systems as an alternative to traditional ID-based models, reframing item recommendation as a sequence generation task over discrete item tokens. While promising, such methods often underperform in practice compared to well-tuned ID-based baselines like SASRec. In this paper, we identify two key limitations holding back generative approaches: the lack of collaborative signal in item tokenization, and inefficiencies in the commonly used encoder-decoder architecture. To address these issues, we introduce COSETTE, a contrastive tokenization method that integrates collaborative information directly into the learned item representations, jointly optimizing for both content reconstruction and recommendation relevance. Additionally, we propose MARIUS, a lightweight, audio-inspired generative model that decouples timeline modeling from item decoding. MARIUS reduces inference cost while improving recommendation accuracy. Experiments on standard sequential recommendation benchmarks show that our approach narrows, or even eliminates, the performance gap between generative and modern ID-based models, while retaining the benefits of the generative paradigm.
Off-policy evaluation (OPE) and off-policy learning (OPL) are foundational for decision-making in offline contextual bandits. Recent advances in OPL primarily optimize OPE estimators with improved statistical properties, assuming that better estimators inherently yield superior policies. Although theoretically justified, we argue this estimator-centric approach neglects a critical practical obstacle: challenging optimization landscapes. In this paper, we provide theoretical insights and extensive empirical evidence showing that current OPL methods encounter severe optimization issues, particularly as action spaces become large. We demonstrate that simpler weighted log-likelihood objectives enjoy substantially better optimization properties and still recover competitive, often superior, learned policies. Our findings emphasize the necessity of explicitly addressing optimization considerations in the development of OPL algorithms for large action spaces.
CORAL is a novel machine learning framework for solving Partial Differential Equations (PDEs) by learning mappings between function spaces on general geometries. It employs modulated Implicit Neural Representations to handle irregular spatial samplings and achieves competitive or superior performance across initial value problems, dynamics modeling, and geometry-aware inference tasks, demonstrating robustness and efficient inference.
Researchers at Criteo AI Lab and CREST developed Diffusion Thompson Sampling (dTS), an algorithm that integrates pre-trained diffusion models as expressive priors into contextual bandits. This method improves online decision-making efficiency, particularly in scenarios with large action spaces and complex dependencies, by outperforming traditional baselines and demonstrating robustness across diverse settings.
Large Language Models (LLMs) often encounter conflicts between their learned,
internal (parametric knowledge, PK) and external knowledge provided during
inference (contextual knowledge, CK). Understanding how LLMs models prioritize
one knowledge source over the other remains a challenge. In this paper, we
propose a novel probing framework to explore the mechanisms governing the
selection between PK and CK in LLMs. Using controlled prompts designed to
contradict the model's PK, we demonstrate that specific model activations are
indicative of the knowledge source employed. We evaluate this framework on
various LLMs of different sizes and demonstrate that mid-layer activations,
particularly those related to relations in the input, are crucial in predicting
knowledge source selection, paving the way for more reliable models capable of
handling knowledge conflicts effectively.
Zebra applies a causal generative transformer with a vector-quantized latent space for in-context learning in parametric PDEs, demonstrating efficient adaptation to unseen dynamics and robust generalization across 1D and 2D problems. The framework achieves orders of magnitude faster inference than gradient-based methods while providing uncertainty quantification and generating new trajectories.
We present AROMA (Attentive Reduced Order Model with Attention), a framework designed to enhance the modeling of partial differential equations (PDEs) using local neural fields. Our flexible encoder-decoder architecture can obtain smooth latent representations of spatial physical fields from a variety of data types, including irregular-grid inputs and point clouds. This versatility eliminates the need for patching and allows efficient processing of diverse geometries. The sequential nature of our latent representation can be interpreted spatially and permits the use of a conditional transformer for modeling the temporal dynamics of PDEs. By employing a diffusion-based formulation, we achieve greater stability and enable longer rollouts compared to conventional MSE training. AROMA's superior performance in simulating 1D and 2D equations underscores the efficacy of our approach in capturing complex dynamical behaviors.
22 Oct 2025
We study reinforcement learning (RL) with transition look-ahead, where the agent may observe which states would be visited upon playing any sequence of ℓ actions before deciding its course of action. While such predictive information can drastically improve the achievable performance, we show that using this information optimally comes at a potentially prohibitive computational cost. Specifically, we prove that optimal planning with one-step look-ahead (ℓ=1) can be solved in polynomial time through a novel linear programming formulation. In contrast, for ℓ≥2, the problem becomes NP-hard. Our results delineate a precise boundary between tractable and intractable cases for the problem of planning with transition look-ahead in reinforcement learning.
In production systems, contextual bandit approaches often rely on direct reward models that take both action and context as input. However, these models can suffer from confounding, making it difficult to isolate the effect of the action from that of the context. We present \emph{Counterfactual Sample Identification}, a new approach that re-frames the problem: rather than predicting reward, it learns to recognize which action led to a successful (binary) outcome by comparing it to a counterfactual action sampled from the logging policy under the same context. The method is theoretically grounded and consistently outperforms direct models in both synthetic experiments and real-world deployments.
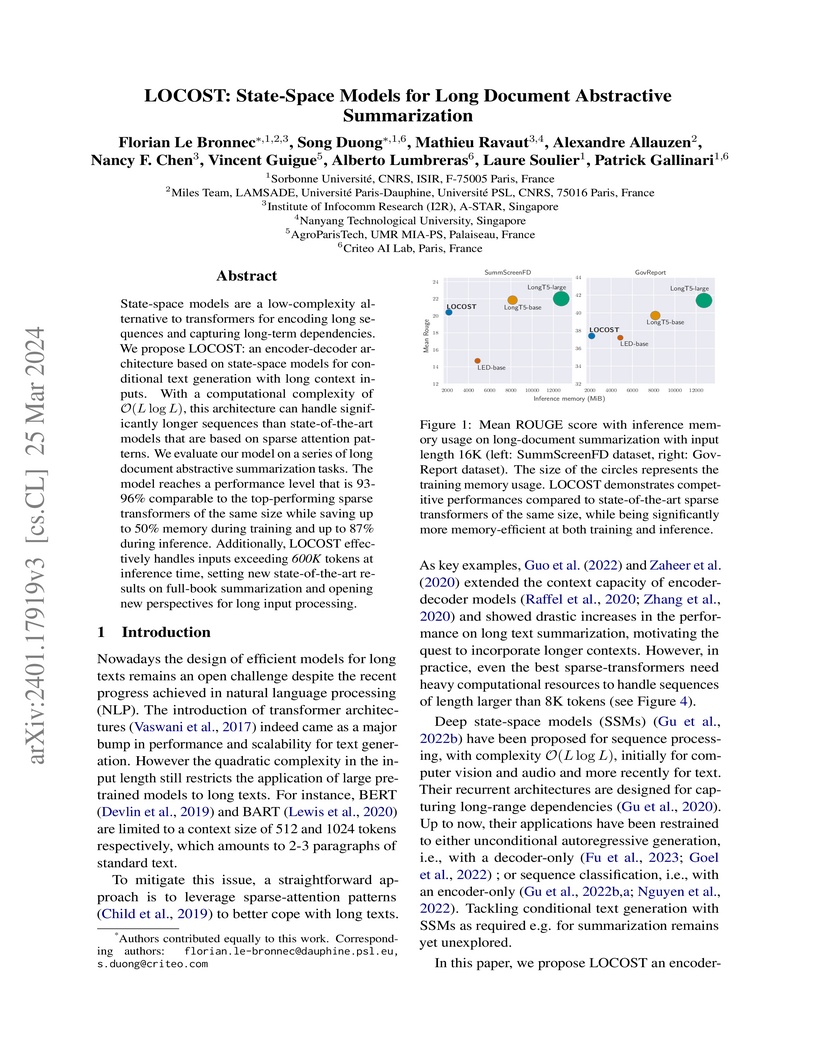
State-space models are a low-complexity alternative to transformers for encoding long sequences and capturing long-term dependencies. We propose LOCOST: an encoder-decoder architecture based on state-space models for conditional text generation with long context inputs. With a computational complexity of O(LlogL), this architecture can handle significantly longer sequences than state-of-the-art models that are based on sparse attention patterns. We evaluate our model on a series of long document abstractive summarization tasks. The model reaches a performance level that is 93-96% comparable to the top-performing sparse transformers of the same size while saving up to 50% memory during training and up to 87% during inference. Additionally, LOCOST effectively handles input texts exceeding 600K tokens at inference time, setting new state-of-the-art results on full-book summarization and opening new perspectives for long input processing.
Consistency models imitate the multi-step sampling of score-based diffusion in a single forward pass of a neural network. They can be learned in two ways: consistency distillation and consistency training. The former relies on the true velocity field of the corresponding differential equation, approximated by a pre-trained neural network. In contrast, the latter uses a single-sample Monte Carlo estimate of this velocity field. The related estimation error induces a discrepancy between consistency distillation and training that, we show, still holds in the continuous-time limit. To alleviate this issue, we propose a novel flow that transports noisy data towards their corresponding outputs derived from a consistency model. We prove that this flow reduces the previously identified discrepancy and the noise-data transport cost. Consequently, our method not only accelerates consistency training convergence but also enhances its overall performance. The code is available at: this https URL.
Solving time-dependent parametric partial differential equations (PDEs) remains a fundamental challenge for neural solvers, particularly when generalizing across a wide range of physical parameters and dynamics. When data is uncertain or incomplete-as is often the case-a natural approach is to turn to generative models. We introduce ENMA, a generative neural operator designed to model spatio-temporal dynamics arising from physical phenomena. ENMA predicts future dynamics in a compressed latent space using a generative masked autoregressive transformer trained with flow matching loss, enabling tokenwise generation. Irregularly sampled spatial observations are encoded into uniform latent representations via attention mechanisms and further compressed through a spatio-temporal convolutional encoder. This allows ENMA to perform in-context learning at inference time by conditioning on either past states of the target trajectory or auxiliary context trajectories with similar dynamics. The result is a robust and adaptable framework that generalizes to new PDE regimes and supports one-shot surrogate modeling of time-dependent parametric PDEs.
In the past years, many proposals have emerged in order to address online advertising use-cases without access to third-party cookies. All these proposals leverage some privacy-enhancing technologies such as aggregation or differential privacy. Yet, no public and rich-enough ground truth is currently available to assess the relevancy of aforementioned private advertising frameworks. We are releasing the largest, in terms of number of features, bidding dataset specifically built in alignment with the design of major browser vendors proposals such as Chrome Privacy Sandbox. This dataset, coined CriteoPrivateAds, stands for an anonymised version of Criteo production logs and provides sufficient data to learn bidding models commonly used in online advertising under many privacy constraints (delayed reports, display and user-level differential privacy, user signal quantisation or aggregated reports). We ensured that this dataset, while being anonymised, is able to provide offline results close to production performance of adtech companies including Criteo - making it a relevant ground truth to design private advertising systems. The dataset is available in Hugging Face: this https URL.
Determinantal point processes (DPPs) have attracted substantial attention as
an elegant probabilistic model that captures the balance between quality and
diversity within sets. DPPs are conventionally parameterized by a positive
semi-definite kernel matrix, and this symmetric kernel encodes only repulsive
interactions between items. These so-called symmetric DPPs have significant
expressive power, and have been successfully applied to a variety of machine
learning tasks, including recommendation systems, information retrieval, and
automatic summarization, among many others. Efficient algorithms for learning
symmetric DPPs and sampling from these models have been reasonably well
studied. However, relatively little attention has been given to nonsymmetric
DPPs, which relax the symmetric constraint on the kernel. Nonsymmetric DPPs
allow for both repulsive and attractive item interactions, which can
significantly improve modeling power, resulting in a model that may better fit
for some applications. We present a method that enables a tractable algorithm,
based on maximum likelihood estimation, for learning nonsymmetric DPPs from
data composed of observed subsets. Our method imposes a particular
decomposition of the nonsymmetric kernel that enables such tractable learning
algorithms, which we analyze both theoretically and experimentally. We evaluate
our model on synthetic and real-world datasets, demonstrating improved
predictive performance compared to symmetric DPPs, which have previously shown
strong performance on modeling tasks associated with these datasets.
In interactive systems, actions are often correlated, presenting an
opportunity for more sample-efficient off-policy evaluation (OPE) and learning
(OPL) in large action spaces. We introduce a unified Bayesian framework to
capture these correlations through structured and informative priors. In this
framework, we propose sDM, a generic Bayesian approach for OPE and OPL,
grounded in both algorithmic and theoretical foundations. Notably, sDM
leverages action correlations without compromising computational efficiency.
Moreover, inspired by online Bayesian bandits, we introduce Bayesian metrics
that assess the average performance of algorithms across multiple problem
instances, deviating from the conventional worst-case assessments. We analyze
sDM in OPE and OPL, highlighting the benefits of leveraging action
correlations. Empirical evidence showcases the strong performance of sDM.
Reinforcement learning (RL) is central to improving reasoning in large language models (LLMs) but typically requires ground-truth rewards. Test-Time Reinforcement Learning (TTRL) removes this need by using majority-vote rewards, but relies on heavy online RL and incurs substantial computational cost. We propose RoiRL: Reasoning with offline iterative Reinforcement Learning, a family of lightweight offline learning alternatives that can target the same regularized optimal policies. Unlike TTRL, RoiRL eliminates the need to maintain a reference model and instead optimizes weighted log-likelihood objectives, enabling stable training with significantly lower memory and compute requirements. Experimental results show that RoiRL trains to 2.5x faster and consistently outperforms TTRL on reasoning benchmarks, establishing a scalable path to self-improving LLMs without labels.
Due to domain shifts, machine learning systems typically struggle to
generalize well to new domains that differ from those of training data, which
is what domain generalization (DG) aims to address. Although a variety of DG
methods have been proposed, most of them fall short in interpretability and
require domain labels, which are not available in many real-world scenarios.
This paper presents a novel DG method, called HMOE: Hypernetwork-based Mixture
of Experts (MoE), which does not rely on domain labels and is more
interpretable. MoE proves effective in identifying heterogeneous patterns in
data. For the DG problem, heterogeneity arises exactly from domain shifts. HMOE
employs hypernetworks taking vectors as input to generate the weights of
experts, which promotes knowledge sharing among experts and enables the
exploration of their similarities in a low-dimensional vector space. We
benchmark HMOE against other DG methods under a fair evaluation framework --
DomainBed. Our extensive experiments show that HMOE can effectively separate
mixed-domain data into distinct clusters that are surprisingly more consistent
with human intuition than original domain labels. Using self-learned domain
information, HMOE achieves state-of-the-art results on most datasets and
significantly surpasses other DG methods in average accuracy across all
datasets.
There are no more papers matching your filters at the moment.