Modern medical image registration approaches predict deformations using deep networks. These approaches achieve state-of-the-art (SOTA) registration accuracy and are generally fast. However, deep learning (DL) approaches are, in contrast to conventional non-deep-learning-based approaches, anatomy-specific. Recently, a universal deep registration approach, uniGradICON, has been proposed. However, uniGradICON focuses on monomodal image registration. In this work, we therefore develop multiGradICON as a first step towards universal *multimodal* medical image registration. Specifically, we show that 1) we can train a DL registration model that is suitable for monomodal *and* multimodal registration; 2) loss function randomization can increase multimodal registration accuracy; and 3) training a model with multimodal data helps multimodal generalization. Our code and the multiGradICON model are available at this https URL

Understanding disaggregate channels in the transmission of monetary policy is of crucial importance for effectively implementing policy measures. We extend the empirical econometric literature on the role of production networks in the propagation of shocks along two dimensions. First, we allow for industry-specific responses that vary over time, reflecting non-linearities and cross-sectional heterogeneities in direct transmission channels. Second, we allow for time-varying network structures and dependence. This feature captures both variation in the structure of the production network, but also differences in cross-industry demand elasticities. We find that impacts vary substantially over time and the cross-section. Higher-order effects appear to be particularly important in periods of economic and financial uncertainty, often coinciding with tight credit market conditions and financial stress. Differentials in industry-specific responses can be explained by how close the respective industries are to end-consumers.

We consider the problem of computing persistent homology (PH) for large-scale Euclidean point cloud data, aimed at downstream machine learning tasks, where the exponential growth of the most widely-used Vietoris-Rips complex imposes serious computational limitations. Although more scalable alternatives such as the Alpha complex or sparse Rips approximations exist, they often still result in a prohibitively large number of simplices. This poses challenges in the complex construction and in the subsequent PH computation, prohibiting their use on large-scale point clouds. To mitigate these issues, we introduce the Flood complex, inspired by the advantages of the Alpha and Witness complex constructions. Informally, at a given filtration value $r\geq 0$, the Flood complex contains all simplices from a Delaunay triangulation of a small subset of the point cloud $X$ that are fully covered by balls of radius $r$ emanating from $X$, a process we call flooding. Our construction allows for efficient PH computation, possesses several desirable theoretical properties, and is amenable to GPU parallelization. Scaling experiments on 3D point cloud data show that we can compute PH of up to dimension 2 on several millions of points. Importantly, when evaluating object classification performance on real-world and synthetic data, we provide evidence that this scaling capability is needed, especially if objects are geometrically or topologically complex, yielding performance superior to other PH-based methods and neural networks for point cloud data.

We study distributed algorithms built around minor-based vertex sparsifiers, and give the first algorithm in the CONGEST model for solving linear systems in graph Laplacian matrices to high accuracy. Our Laplacian solver has a round complexity of $O(n^{o(1)}(\sqrt{n}+D))$, and thus almost matches the lower bound of $\widetilde{\Omega}(\sqrt{n}+D)$, where $n$ is the number of nodes in the network and $D$ is its diameter. We show that our distributed solver yields new sublinear round algorithms for several cornerstone problems in combinatorial optimization. This is achieved by leveraging the powerful algorithmic framework of Interior Point Methods (IPMs) and the Laplacian paradigm in the context of distributed graph algorithms, which entails numerically solving optimization problems on graphs via a series of Laplacian systems. Problems that benefit from our distributed algorithmic paradigm include exact mincost flow, negative weight shortest paths, maxflow, and bipartite matching on sparse directed graphs. For the maxflow problem, this is the first exact distributed algorithm that applies to directed graphs, while the previous work by [Ghaffari et al. SICOMP'18] considered the approximate setting and works only for undirected graphs. For the mincost flow and the negative weight shortest path problems, our results constitute the first exact distributed algorithms running in a sublinear number of rounds. Given that the hybrid between IPMs and the Laplacian paradigm has proven useful for tackling numerous optimization problems in the centralized setting, we believe that our distributed solver will find future applications.

We consider the foundational problem of maintaining a $(1-\varepsilon)$-approximate maximum weight matching (MWM) in an $n$-node dynamic graph undergoing edge insertions and deletions. We provide a general reduction that reduces the problem on graphs with a weight range of $\mathrm{poly}(n)$ to $\mathrm{poly}(1/\varepsilon)$ at the cost of just an additive $\mathrm{poly}(1/\varepsilon)$ in update time. This improves upon the prior reduction of Gupta-Peng (FOCS 2013) which reduces the problem to a weight range of $\varepsilon^{-O(1/\varepsilon)}$ with a multiplicative cost of $O(\log n)$. When combined with a reduction of Bernstein-Dudeja-Langley (STOC 2021) this yields a reduction from dynamic $(1-\varepsilon)$-approximate MWM in bipartite graphs with a weight range of $\mathrm{poly}(n)$ to dynamic $(1-\varepsilon)$-approximate maximum cardinality matching in bipartite graphs at the cost of a multiplicative $\mathrm{poly}(1/\varepsilon)$ in update time, thereby resolving an open problem in [GP'13; BDL'21]. Additionally, we show that our approach is amenable to MWM problems in streaming, shared-memory work-depth, and massively parallel computation models. We also apply our techniques to obtain an efficient dynamic algorithm for rounding weighted fractional matchings in general graphs. Underlying our framework is a new structural result about MWM that we call the "matching composition lemma" and new dynamic matching subroutines that may be of independent interest.

The top-k classification accuracy is one of the core metrics in machine learning. Here, k is conventionally a positive integer, such as 1 or 5, leading to top-1 or top-5 training objectives. In this work, we relax this assumption and optimize the model for multiple k simultaneously instead of using a single k. Leveraging recent advances in differentiable sorting and ranking, we propose a differentiable top-k cross-entropy classification loss. This allows training the network while not only considering the top-1 prediction, but also, e.g., the top-2 and top-5 predictions. We evaluate the proposed loss function for fine-tuning on state-of-the-art architectures, as well as for training from scratch. We find that relaxing k does not only produce better top-5 accuracies, but also leads to top-1 accuracy improvements. When fine-tuning publicly available ImageNet models, we achieve a new state-of-the-art for these models.

We study the distributional implications of uncertainty shocks by developing a model that links macroeconomic aggregates to the US distribution of earnings and consumption. We find that: initially, the fraction of low-earning workers decreases, while the share of households reporting low consumption increases; at longer horizons, the fraction of low-income workers increases, but the consumption distribution reverts to its pre-shock shape. While the first phase reduces income inequality and increases consumption inequality, in the second stage income inequality rises, while the effects on consumption inequality dissipate. Finally, we introduce Functional Local Projections and show that they yield similar results.

In this work, a novel multi-face tracking method named FaceQSORT is proposed. To mitigate multi-face tracking challenges (e.g., partially occluded or lateral faces), FaceQSORT combines biometric and visual appearance features (extracted from the same image (face) patch) for association. The Q in FaceQSORT refers to the scenario for which FaceQSORT is desinged, i.e. tracking people's faces as they move towards a gate in a Queue. This scenario is also reflected in the new dataset `Paris Lodron University Salzburg Faces in a Queue', which is made publicly available as part of this work. The dataset consists of a total of seven fully annotated and challenging sequences (12730 frames) and is utilized together with two other publicly available datasets for the experimental evaluation. It is shown that FaceQSORT outperforms state-of-the-art trackers in the considered scenario. To provide a deeper insight into FaceQSORT, comprehensive experiments are conducted evaluating the parameter selection, a different similarity metric and the utilized face recognition model (used to extract biometric features).

Approximate nearest neighbor (ANN) search is a fundamental problem in computer science for which in-memory graph-based methods, such as Hierarchical Navigable Small World (HNSW), perform exceptionally well. To scale beyond billions of high-dimensional vectors, the index must be distributed. The disaggregated memory architecture physically separates compute and memory into two distinct hardware units and has become popular in modern data centers. Both units are connected via RDMA networks that allow compute nodes to directly access remote memory and perform all the computations, posing unique challenges for disaggregated indexes. In this work, we propose a scalable HNSW index for ANN search in disaggregated memory. In contrast to existing distributed approaches, which partition the graph at the cost of accuracy, our method builds a graph-preserving index that reaches the same accuracy as a single-machine HNSW. Continuously fetching high-dimensional vector data from remote memory leads to severe network bandwidth limitations, which we overcome by employing an efficient caching mechanism. Since answering a single query involves processing numerous unique graph nodes, caching alone is not sufficient to achieve high scalability. We logically combine the caches of the compute nodes to increase the overall cache effectiveness and confirm the efficiency and scalability of our method in our evaluation.

Macroeconomic data is characterized by a limited number of observations (small T), many time series (big K) but also by featuring temporal dependence. Neural networks, by contrast, are designed for datasets with millions of observations and covariates. In this paper, we develop Bayesian neural networks (BNNs) that are well-suited for handling datasets commonly used for macroeconomic analysis in policy institutions. Our approach avoids extensive specification searches through a novel mixture specification for the activation function that appropriately selects the form of nonlinearities. Shrinkage priors are used to prune the network and force irrelevant neurons to zero. To cope with heteroskedasticity, the BNN is augmented with a stochastic volatility model for the error term. We illustrate how the model can be used in a policy institution by first showing that our different BNNs produce precise density forecasts, typically better than those from other machine learning methods. Finally, we showcase how our model can be used to recover nonlinearities in the reaction of macroeconomic aggregates to financial shocks.

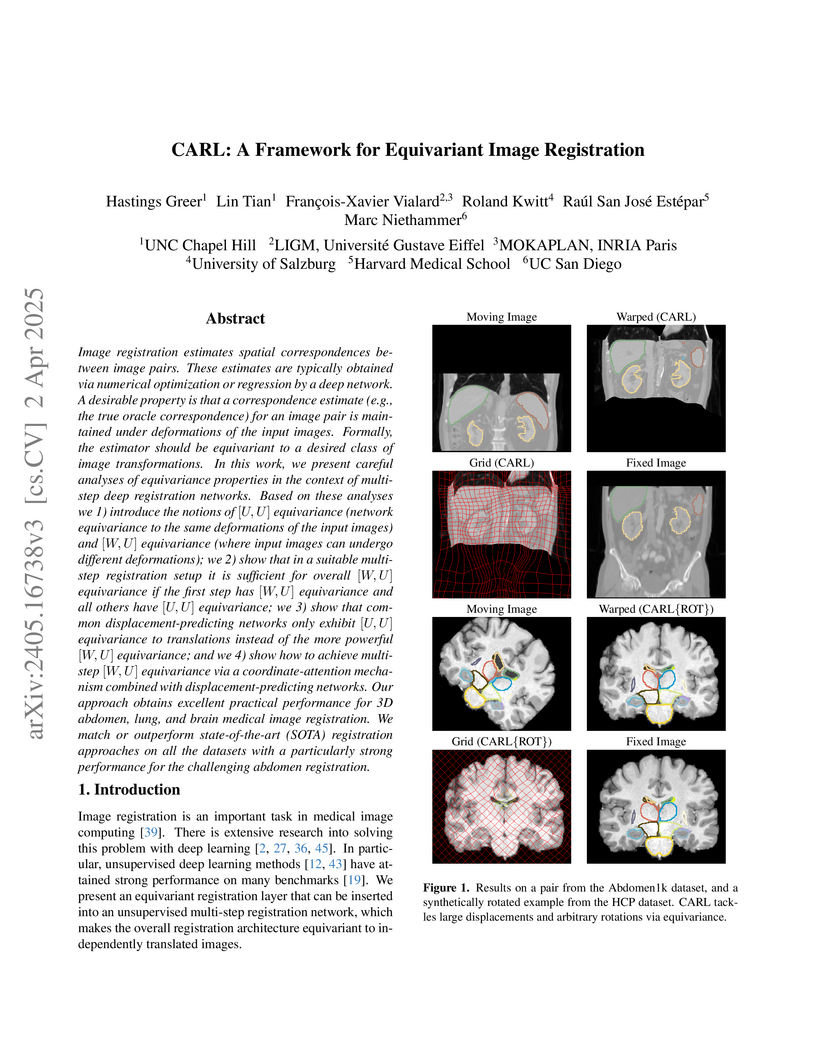
Image registration estimates spatial correspondences between a pair of images. These estimates are typically obtained via numerical optimization or regression by a deep network. A desirable property of such estimators is that a correspondence estimate (e.g., the true oracle correspondence) for an image pair is maintained under deformations of the input images. Formally, the estimator should be equivariant to a desired class of image transformations. In this work, we present careful analyses of the desired equivariance properties in the context of multi-step deep registration networks. Based on these analyses we 1) introduce the notions of $[U,U]$ equivariance (network equivariance to the same deformations of the input images) and $[W,U]$ equivariance (where input images can undergo different deformations); we 2) show that in a suitable multi-step registration setup it is sufficient for overall $[W,U]$ equivariance if the first step has $[W,U]$ equivariance and all others have $[U,U]$ equivariance; we 3) show that common displacement-predicting networks only exhibit $[U,U]$ equivariance to translations instead of the more powerful $[W,U]$ equivariance; and we 4) show how to achieve multi-step $[W,U]$ equivariance via a coordinate-attention mechanism combined with displacement-predicting refinement layers (CARL). Overall, our approach obtains excellent practical registration performance on several 3D medical image registration tasks and outperforms existing unsupervised approaches for the challenging problem of abdomen registration.

The integration of algorithmic components into neural architectures has gained increased attention recently, as it allows training neural networks with new forms of supervision such as ordering constraints or silhouettes instead of using ground truth labels. Many approaches in the field focus on the continuous relaxation of a specific task and show promising results in this context. But the focus on single tasks also limits the applicability of the proposed concepts to a narrow range of applications. In this work, we build on those ideas to propose an approach that allows to integrate algorithms into end-to-end trainable neural network architectures based on a general approximation of discrete conditions. To this end, we relax these conditions in control structures such as conditional statements, loops, and indexing, so that resulting algorithms are smoothly differentiable. To obtain meaningful gradients, each relevant variable is perturbed via logistic distributions and the expectation value under this perturbation is approximated. We evaluate the proposed continuous relaxation model on four challenging tasks and show that it can keep up with relaxations specifically designed for each individual task.

We consider the training of the first layer of vision models and notice the clear relationship between pixel values and gradient update magnitudes: the gradients arriving at the weights of a first layer are by definition directly proportional to (normalized) input pixel values. Thus, an image with low contrast has a smaller impact on learning than an image with higher contrast, and a very bright or very dark image has a stronger impact on the weights than an image with moderate brightness. In this work, we propose performing gradient descent on the embeddings produced by the first layer of the model. However, switching to discrete inputs with an embedding layer is not a reasonable option for vision models. Thus, we propose the conceptual procedure of (i) a gradient descent step on first layer activations to construct an activation proposal, and (ii) finding the optimal weights of the first layer, i.e., those weights which minimize the squared distance to the activation proposal. We provide a closed form solution of the procedure and adjust it for robust stochastic training while computing everything efficiently. Empirically, we find that TrAct (Training Activations) speeds up training by factors between 1.25x and 4x while requiring only a small computational overhead. We demonstrate the utility of TrAct with different optimizers for a range of different vision models including convolutional and transformer architectures.

Depression is a significant issue nowadays. As per the World Health Organization (WHO), in 2023, over 280 million individuals are grappling with depression. This is a huge number; if not taken seriously, these numbers will increase rapidly. About 4.89 billion individuals are social media users. People express their feelings and emotions on platforms like Twitter, Facebook, Reddit, Instagram, etc. These platforms contain valuable information which can be used for research purposes. Considerable research has been conducted across various social media platforms. However, certain limitations persist in these endeavors. Particularly, previous studies were only focused on detecting depression and the intensity of depression in tweets. Also, there existed inaccuracies in dataset labeling. In this research work, five types of depression (Bipolar, major, psychotic, atypical, and postpartum) were predicted using tweets from the Twitter database based on lexicon labeling. Explainable AI was used to provide reasoning by highlighting the parts of tweets that represent type of depression. Bidirectional Encoder Representations from Transformers (BERT) was used for feature extraction and training. Machine learning and deep learning methodologies were used to train the model. The BERT model presented the most promising results, achieving an overall accuracy of 0.96.

A tree-packing is a collection of spanning trees of a graph. It has been a useful tool for computing the minimum cut in static, dynamic, and distributed settings. In particular, [Thorup, Comb. 2007] used them to obtain his dynamic min-cut algorithm with $\tilde O(\lambda^{14.5}\sqrt{n})$ worst-case update time. We reexamine this relationship, showing that we need to maintain fewer spanning trees for such a result; we show that we only need to pack $\Theta(\lambda^3 \log m)$ greedy trees to guarantee a 1-respecting cut or a trivial cut in some contracted graph. Based on this structural result, we then provide a deterministic algorithm for fully dynamic exact min-cut, that has $\tilde O(\lambda^{5.5}\sqrt{n})$ worst-case update time, for min-cut value bounded by $\lambda$. In particular, this also leads to an algorithm for general fully dynamic exact min-cut with $\tilde O(m^{1-1/12})$ amortized update time, improving upon $\tilde O(m^{1-1/31})$ [Goranci et al., SODA 2023]. We also give the first fully dynamic algorithm that maintains a $(1+\varepsilon)$-approximation of the fractional arboricity -- which is strictly harder than the integral arboricity. Our algorithm is deterministic and has $O(\alpha \log^6m/\varepsilon^4)$ amortized update time, for arboricity at most $\alpha$. We extend these results to a Monte Carlo algorithm with $O(\text{poly}(\log m,\varepsilon^{-1}))$ amortized update time against an adaptive adversary. Our algorithms work on multi-graphs as well. Both result are obtained by exploring the connection between the min-cut/arboricity and (greedy) tree-packing. We investigate tree-packing in a broader sense; including a lower bound for greedy tree-packing, which - to the best of our knowledge - is the first progress on this topic since [Thorup, Comb. 2007].

We propose a new approach for propagating stable probability distributions through neural networks. Our method is based on local linearization, which we show to be an optimal approximation in terms of total variation distance for the ReLU non-linearity. This allows propagating Gaussian and Cauchy input uncertainties through neural networks to quantify their output uncertainties. To demonstrate the utility of propagating distributions, we apply the proposed method to predicting calibrated confidence intervals and selective prediction on out-of-distribution data. The results demonstrate a broad applicability of propagating distributions and show the advantages of our method over other approaches such as moment matching.

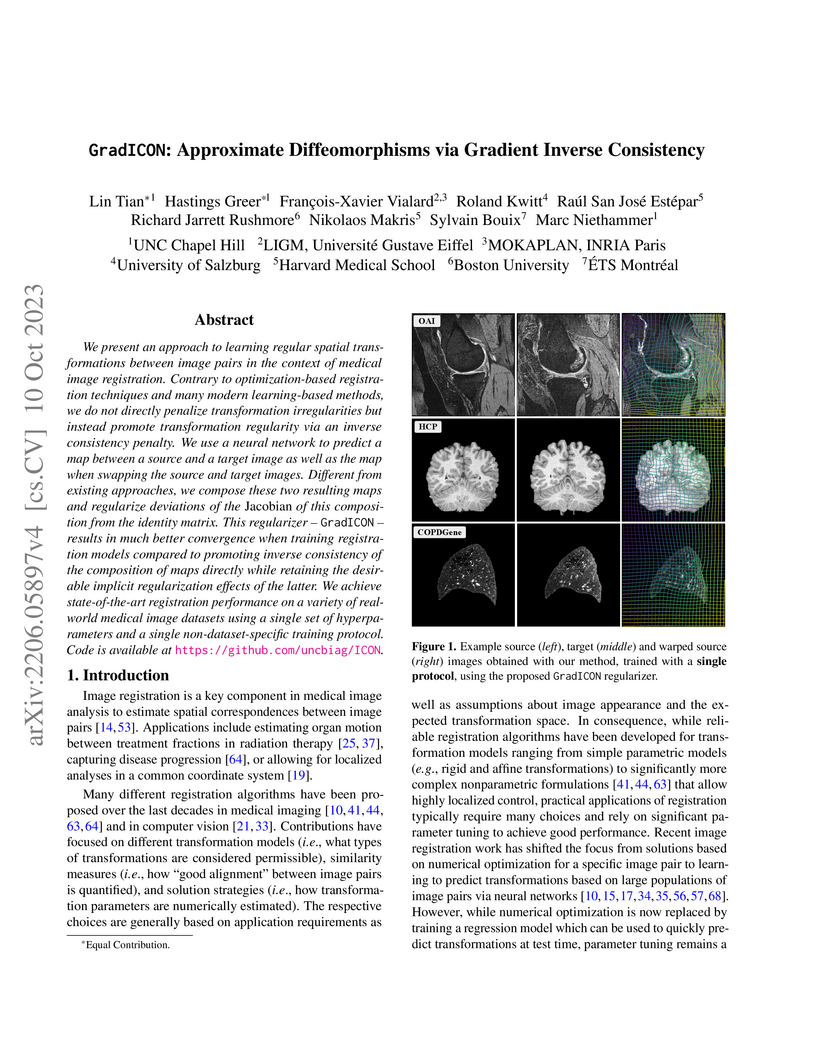
We present an approach to learning regular spatial transformations between image pairs in the context of medical image registration. Contrary to optimization-based registration techniques and many modern learning-based methods, we do not directly penalize transformation irregularities but instead promote transformation regularity via an inverse consistency penalty. We use a neural network to predict a map between a source and a target image as well as the map when swapping the source and target images. Different from existing approaches, we compose these two resulting maps and regularize deviations of the $\bf{Jacobian}$ of this composition from the identity matrix. This regularizer -- $\texttt{GradICON}$ -- results in much better convergence when training registration models compared to promoting inverse consistency of the composition of maps directly while retaining the desirable implicit regularization effects of the latter. We achieve state-of-the-art registration performance on a variety of real-world medical image datasets using a single set of hyperparameters and a single non-dataset-specific training protocol.